Образовательный блог — всё для учебы

Многие важные задачи анализа систем могут быть сформулированы в терминах момента первого достижения. Поэтому различные оценки распределения этого момента важны в первую очередь с практической точки зрения.

Сформулируем задачу, которая будет решаться в данной главе.
Прочитать остальную часть записи »

Без потери общности предположим, что решается задача минимизации унимодальной функции Q (х), определенной на единичном интервале [0, 1], во внутренней точке ξ которого имеется информация о численном значении функции Q (ξ). В этом случае применение процедур сокращения интервала неопределенности позволяет получить после проведения N испытаний апостериорный интервал неопределенности [a_N, b_N], длина которого определяется следующим выражением:

l_N(ξ) = b_N — a_N = max ((1-ξ)/u_N, ξ/u_N-1), 0 ≤ ξ ≤ 1/2; (3.61)

Прочитать остальную часть записи »

Особенности работы локальной сети в режиме файл сервер

Возможность одновременного доступа к общим данным является достаточно хорошим техническим решением для группы пользователей, однако для этого нужно соблюсти некоторые вещи, чтобы некоторая ограниченная группа пользователей могла параллельно иметь доступ и заботилась о целостности данных. Здесь решаются следующие основные общие проблемы:
Прочитать остальную часть записи »

Пример 1. Процесс рождения и гибели. Рассмотрим вероятностный процесс, широко применяемый в различных прикладных областях. Это процесс со счетным числом состояний N = {0, 1, 2, …}. В каждом состоянии v∈N процесс проводит случайное время, которое распределено экспоненциально с параметром λ(v), после чего переходит либо в состояние v + 1 (с вероятностью p_v), либо в состояние v—1 (с вероятностью q_v), q₀ = 0, p_v + q_v = 1. Будем считать, что λ(v) > 0, v ≥ 0, p_v > 0, v ≥ 0 и q_v > 0, v ≥ 1. Из этих условий следует, что p₀ = 1. Величина λ(v)p_v трактуется как интенсивность рождения в состоянии v, а λ(v)q_v — интенсивность гибели в этом же состоянии. Очевидно, что любая функция V(v), не принимающая бесконечных значений, принадлежит множеству D_А. При этом вид оператора А (см. формулу (3.4), где нужно положить v_v = 0) следующий:

AV(v) = λ(v) [p_vV(v + 1) + q_vV(v- 1) — V(v)]. (1)

Прочитать остальную часть записи »

Метод поиска, реализующий процедуру выбора точек испытаний по формулам (3.8)—(3.9) (см. предыдущий пост) коэффициентами t_k*, которые вычисляются из выражений (3.37), называется методом Фибоначчи. Это название возникло в связи с тем, что стратегия поиска оптимального решения х* по данному методу, как нетрудно видеть, связана с использованием чисел Фибоначчи (3.29).
Прочитать остальную часть записи »

Объектом изучения в данном посте и далее, если не оговорено противное, является процесс z_t, построенный на последовательности необрывающихся процессов z_{t, n}. Напомним, что одним из условий проведенных построений является необрываемость подпроцессов z_{t, n}. В свою очередь достаточным условием для этого является выполнение леммы 2 с заменой Т_δ на T_{δ, n}. Ниже без дополнительных оговорок будет считаться, что все подпроцессы z_{t, n} необрывающиеся. Во всех примерах данной и последующих постов условия леммы 2 выполнены. Это обстоятельство также не будет всякий раз оговариваться.
Прочитать остальную часть записи »

Задача минимизации одномерной унимодальной функции Q(х), определенной на интервале [а, b], связана с поиском оптимального решения х*:

Q(x*)= min Q(x). (3.1)

Из свойства унимодальности функции Q (х) следует, что с возрастанием переменной х функция Q (х) строго убывает при х ≤ х* и строго возрастает при х ≥ х*, т. е. унимодальная функция не должна иметь горизонтальных участков («плато»), хотя может быть не дифференцируемой, разрывной, неопределенной в некоторых точках и т. д. В начале поиска положение точки х* на интервале [а, b] неизвестно. Путем проведения в точках рассматриваемого интервала N испытаний требуется локализовать оптимальное решение х* в интервале [a_N, b_N] меньшей длины, чем исходный. При этом предполагается, что каждое испытание, связанное с вычислением значения функции Q (х), может быть выполнено без ошибки, либо последняя настолько мала, что ею можно пренебречь. В дальнейшем интервал [a_N, b_N] будем называть апостериорным интервалом неопределенности в отличие от исходного интервала [а, b], называемого априорным интервалом неопределенности.
Прочитать остальную часть записи »

Условия леммы 1 достаточны для того, чтобы рассматриваемые процессы были необрывающимися. Однако существуют практически интересные задачи, требующие изучения процессов, у которых функции λ(z) и v^v неограничены. Поэтому принципильно важно получить более широкие условия регулярности рассматриваемых процессов. Вместе с тем необходимо напомнить, что построения были проведены в предположении равномерной ограниченности λ(z) и v^v (условие (1.3.2)). Поэтому, прежде чем переходить к получению соответствующих результатов, необходимо расширить класс изучаемых процессов.
Прочитать остальную часть записи »

Имитационная модель задается из совокупности моделей отдельных компонентов системы и связей между ними. Но составление моделей — не самоцель. Модель требуется для реализации машинных экспериментов. Таким образом, после создания модели системы из компонентов надо иметь средства для организации различных экспериментов с ней. Кроме того, необходимо в удобном виде представить результаты эксперимента для их анализа.
Прочитать остальную часть записи »

Для неравноценных частных критериев Q_i, i = 1, …, s, значения весовых коэффициентов λ_i, i = 1, …, s, выбираются в соответствии с важностью критерия (более предпочтительному критерию соответствует большее значение весового коэффициента) таким образом, чтобы выполнялось условие

λ_i ≥ 0, i = 1, 2, .., s; ∑λ_i = 1. (2.81)

Прочитать остальную часть записи »

Вводные замечания
Необходимость изучения свойства регулярности возникает естественным образом при рассмотрении возможных типов поведения динамических (в широком смысле) систем. Оказывается, что при определенных условиях траектории могут за конечное время «уйти в бесконечность» или иметь бесконечное число скачков. Такое поведение обычно рассматривается как нежелательное или невозможное, поскольку в реальных системах уход координат в бесконечность за конечное время требует либо бесконечной мощности, либо бесконечной интенсивности расхода других ресурсов. Кроме того, со свойством регулярности тесно связаны и другие качественные свойства — ограниченность, устойчивость и свойства, определяемые моментами первого достижения и возвращения.
Прочитать остальную часть записи »

Идея этого метода заключается в том, что на каждом k-м шаге последовательной оптимизации вводится уступка ΔQ_k-1, характеризующая допустимое отклонение (k — 1)-го частного критерия от его минимального значения:

Q₁(x₁*) = min Q₁(x); Q_k(x_k*) = min Q_k(x), (2.45)

где

D_k = D∩D_k-1; D_k-1 = {x|Q_j(x) ≤ Q_j(x_j*) + ΔQ_j, j = 1, 2, …, k-1}.

Прочитать остальную часть записи »

Анализ состава и структуры дебиторской задолженности

Вывод: на конец года коэффициент оборачиваемости = 14,41 т.е. 14 раз за год предприятию поступают денежные средства от покупателей за проданную продукцию. При этом период погашения = 24,64 дня. Наблюдается замедление оборачиваемости дебиторской задолженности за год. Период погашения увеличился больше, чем на 2 дня. Доля дебиторской задолженности на конец года уменьшилась незначительно и составила 9% в общем объеме оборотных активов (укладывается до 40%, что является рациональным изменением). Удельный вес дебиторской задолженности в объеме реализации увеличился на 0,68% на конец года, и составил 6,75%, т.е. на 1 рубль выручки приходится приблизительно 6,8 копейки обязательств покупателей. Сомнительная дебиторская задолженность отсутствует.
Прочитать остальную часть записи »

Пусть уравнения возмущенного движения имеют вид

dx/dt = F(x), F(0) = 0, x(t₀) = x₀. (3.5.1)

Определение 5. Производной dV/dt функции V(x) = V(x₁, x₂, …, x_N) в силу уравнений возмущенного движения (1.18) называется ее полная производная по времени, вычисленная в предположении, что величины x₁, x₂, …, x_N удовлетворяют уравнениям (1.18), т.е.
Прочитать остальную часть записи »

Многолинейная система обслуживания с ожиданием. Дадим теперь пример системы, по конструкции более простой, чем КЛП Гнеденко — Коваленко, но не укладывающейся в эту схему.

Рассмотрим систему массового обслуживания (в другом представлении она была рассмотрена в примере 3), состоящую из N приборов, на которую через независимые одинаково распределенные случайные промежутки времени поступают требования. Обозначим Н(х) функцию распределения этих промежутков. Длительности обслуживания отдельных требований на приборах не зависят от остальных случайных величин, «управляющих» системой, и имеют одну и ту же (для всех приборов и требований) функцию распределения В(х). Будем характеризовать состояние системы вектором z = (v, z^v), v = 0, 1, …, где компоненты вектора z имеют следующий смысл: v — число требований, находящихся в системе, z^v(1)—время, оставшееся до поступления очередного требования,
z^v(j), 1 < j ≤ N ∧ v + 1 — времена, оставшиеся до окончания обслуживании требований, находящихся на приборах. Прочитать остальную часть записи »

Предположим, что информация о важности частных критериев оптимальности Q_i (х), i = 1, 2, …, s задана в виде ряда приоритетов — множества индексов J = (1, 2, …, s), упорядочивающих частные критерии в порядке убывания их важности:

Q₁ > Q₂ > … > Q_s (2.39)

Прочитать остальную часть записи »

Модель узла связи как КЛП Гнеденко — Коваленко. Предварим разбор примера кратким описанием системы. Рассмотрим сеть связи, задаваемую некоторым графом (рис. 2).

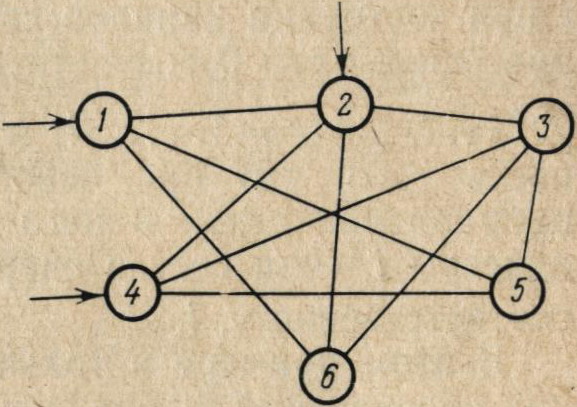
Рис. 2

Узлы графа соответствуют узлам связи, а дуги — направлениям связи. Система работает следующим образом. В не-которые моменты времени на отдельные узлы связи (на рис. 2 они отмечены номерами 1, 2, 4) извне поступают сообщения, подлежащие передаче по сети. Сообщения характеризуются, вообще говоря, рядом признаков: адресом, приоритетом, предельным сроком нахождения в сети и т. д. Узел связи в соответствии с алгоритмом своей работы либо посылает это сообщение в одно из примыкающих к нему направлений связи, либо запоминает его и хранит до ближайшего момента времени, когда появится возможность послать его в сеть. Указанные альтернативы определяются загрузкой сети, наличием свободных каналов связи и пр. Таким образом, в узле связи могут образовываться очереди из сообщений, ждущих своей отправки.

Рассмотрим узел связи вместе с выходящими из него направлениями связи. Пусть работа узла определяется алгоритмом A. Величины, которые характеризуют этот алгоритм, будем отмечать буквой A. Предположим, что рассматриваемый узел связи может посылать сообщения в R направлений связи, R ≥ 1, причем r-е направление (1 ≤ r ≤ R) состоит из m_r каналов связи. По каждому из каналов связи одновременно может передаваться не более одного сообщения.
Прочитать остальную часть записи »

Рассмотрим значения векторного критерия Q = (Q₁,…, Q_s) в точках х^k и х^l принадлежащие области компромиссов D_k:

Q^k = Q (х^k) = (Q₁^k, Q₂^k, …, Q_s^k) и Q^l = Q (х^l) = (Q₁^l, Q₂^l, …, Q_s^l). (2.11)

Прочитать остальную часть записи »

Многолинейная система массового обслуживания с относительным приоритетом. Дадим пример описания конкретной системы обслуживания в виде КЛП Гнеденко—Коваленко.

Пусть в систему, состоящую из N обслуживающих приборов, поступают требования двух типов. Требования первого типа назовем приоритетными, а второго — обычными. Обслуживание однотипных требований происходит в порядке их поступления, и процесс обслуживания каждого требования идет без прерывания. В случае, если в момент поступления какого-либо требования имеется хотя бы один свободный прибор, оно немедленно начинает обслуживаться. В противном случае требование ожидает начала обслуживания. Если в момент освобождения прибора в системе находится хотя бы одно требование, то на обслуживание поступает требование наивысшего приоритета из имеющихся в системе. Если в некоторый момент в системе находятся v₁ приоритетных и v₂ обычных требований, то с интенсивностью Λ₁(v₁, v₂) поступают приоритетные, а с интенсивностью Λ₂(v₁, v₂) —обычные требования. Это означает, что при фиксированных v₁ и v₂ потоки поступающих приоритетных и обычных требований — независимые пуассоновские с параметрами Λ₁ и Λ₂ соответственно. В такую модель укладываются, в частности, схемы с бесконечными и конечными источниками требований. Обозначим Λ(v₁, v₂) = Λ₁(v₁, v₂) + Λ₂(v₁, v₂), p_i(v₁, v₂) = Λ_i(v₁, v₂) [Λ(v₁, v₂)]^-1, i = 1, 2. Пусть длительности обслуживания отдельных требований — случайные величины, не зависящие ни от процесса поступления, ни от длительностей обслуживания остальных требований. Обозначим через B_i(x) функции распределения длительностей обслуживания требований i-ro типа, i = 1,2.
Прочитать остальную часть записи »

Определение: Двойственной функцией для f(x₁, x₁,…,x_n) называется функция f* = ¬f(¬x₁, ¬x₂,…,¬x_n)

Замечание: (f¬(x₁, x₂,…,x_n))* = (¬f(¬x₁, ¬x₂,…,¬x_n))* = ¬f(¬¬x₁, ¬¬x₂,…,¬¬x_n) = f(x₁, x₂,…,x_n) ⇒ (f*) = f.
Прочитать остальную часть записи »

1. Причиной многокритериальности является необходимость обеспечения оптимальности проектируемого устройства при различных условиях его функционирования, т. е. обеспечение экстремальных значений критерия оптимальности при неопределенности условий, в которых приходится работать устройству. При этом неопределенность может иметь либо количественный характер, выраженный с помощью параметра v, что приводит к задаче оптимизации вида
Прочитать остальную часть записи »

Пример 1. КЛП Гнеденко — Коваленко.

Рассмотрим случайный марковский процесс, служащий моделью широкого класса систем массового обслуживания. Состоянием процесса является вектор z переменной размерности, z = (v, z^v (1), …, z^v(|v|)), где компонента v (основное состояние) принимает значения из конечного или счетного множества N, a z^v(j) > 0, j= 1,…,|v|. В промежутках между скачками z^v(j) изменяется с постоянной скоростью v^v(j). Скачки у этого процесса бывают двух типов. Скачки первого типа (вследствие непрерывного вмешательства случая) происходят с интенсивностью λ(v), зависящей лишь от v. В этом случае после скачка новое основное состояние μ будет случайным с распределением {p_vμ}, ∑p_vμ=1, зависящим лишь от прежнего основного состояния. Таким образом, при рассматриваемом скачке размерность вектора z может только увеличиться. Новый вектор дополнительных координат z* при этом составляется из старого вектора z" и случайного не зависящего от предыстории процесса z, положительного вектора ξ^vμ размерности |μ| — |v|, функция распределения которого H_vμ (х (1), …, х (|μ| — |v|), х (j) > 0, зависит только от v и μ. Именно z^μ = (z^v, ξ^μ) = (z^v(1), …, z^v(|v|), ξ^vμ (1), …, ξ^vμ(|μ|— |v|)). После такого скачка координаты вектора z^μ вновь изменяются с постоянной скоростью v^μ.
Прочитать остальную часть записи »

По способу сжигания топлива различают топки:
• Со слоевым сжиганием:

     — Исторически первый способ

     — Изначально было сжигание в неподвижном первом слое. Куски топлива забрасывались на решетку, через которую внизу пропускался воздушный поток. Много раз совершенствовалась.
Прочитать остальную часть записи »

Наиболее общей математической моделью принятия оптимального решения является задача многокритериальной оптимизации (1.47)— (1.49), в которой требуется найти минимум одновременно по всем компонентам векторного критерия Q = (Q₁, Q₂, …, Q_s). Естественно возникают вопросы: в чем природа такой модели принятия решения и насколько часто она встречается в задачах схемотехнического проектирования электронных схем. Для ответа на них рассмотрим различные классы задач оптимального проектирования и выясним причины, которые приводят к необходимости использовать там векторный критерий оптимальности.
Прочитать остальную часть записи »

Установим теперь для КЛП формулу, аналогичную формуле (1.3). Пусть V(z)—некоторая ограниченная функция, такая, что V(v, z^v+v^vt), рассматриваемая как функция t при z^v+v^vt∈Г_v, непрерывна и обладает непрерывной справа правой производной. Доопределим V(z) на Z* по непрерывности следующим образом: пусть z* = (v, z_*^v)∈Z*, и пусть последовательность {t_i}_i≥1 сходится к 0 и обладает тем свойством, что z_*^v + v^vt_i∈Г_v, i≥1; тогда положим V (z*) = lim V (v, z_*^v + v^vt_i); если же последовательности, обладающей указанным свойством, не существует, то в таких точках z* функцию V доопределим произвольно — такая точка z* недостижима. Обозначим класс полученных функций D_А и будем предполагать, что V∈D_А.
Прочитать остальную часть записи »

Основная области памяти СУБД Oracle:

• Область программного кода. Это ПО, которое предназначено для работы с самой БД.

• SGA (System Global Area) – Системная глобальная область. Это область считается основной в СУБД Oracle. Она хранит данные, используемые совместно всеми процессами в экземпляре. Формально можно делить ее на части: буферный кеш – содержит записи БД, ожидающие перезаписи на диск или доступные для чтения (считанные), буфер журнала обновления, который хранит копии транзакций, которые тоже ждут записи на диск
Прочитать остальную часть записи »

Условия оптимальности для задачи выпуклого программирования (1.30) называются условиями Куна — Таккера и эквивалентны утверждению, что при движении в любом возможном направлении S из точки х* критерий оптимальности Q(x) не может быть уменьшен. Геометрическая интерпретация условий Куна—Таккера имеет следующий смысл: в точке х*∈D , являющейся оптимальным решением задачи выпуклого программирования (1.30), градиент выпуклой функции Q (х) является линейной комбинацией градиентов активных ограничений g_i (х) = b_i, i∈J^—, взятых с положительными коэффициентами u_i* > 0. Условие (1.78) называется условием дополняющей нежесткости и означает, что если некоторое из. неравенств является в точке х*∈D неактивным ограничением, то оно должно входить в условия Куна—Таккера с множителем u_i*, равным нулю, а для активных ограничений множители u_i* должны быть положительными.
Прочитать остальную часть записи »

Один из способов анализа немарковского процесса состоит в расширении пространства его состояний, для того, чтобы включить в понятие состояния всю ту информацию о предыстории исходного процесса, которой полностью определяется его будущее течение. Иногда такая информация может быть задана в виде конечномерного вектора. Именно такому способу анализа немарковских процессов и обязана своим возникновением схема кусочно-линейных марковских процессов (КЛП).
Прочитать остальную часть записи »

Для описания и анализа дискретных систем, решения разностных и рекуррентных уравнений используется Z -преобразование.

Z-преобразование применяют к сигналу, квантованному по времени (к дискретным значениям непрерывного сигнала).

Z -преобразование определяется как сумма отрицательных степеней комплексной переменной z с помощью соотношения:

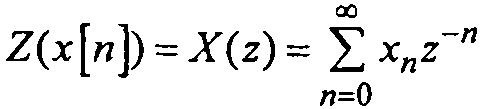(1.18)

Сформулируем теперь условия оптимальности для задачи условной оптимизации (1.32).

Предположим, что ограничения g_i (х) являются непрерывными дифференцируемыми функциями и уравнения связи g_i(х) =b_i, i = 1,2,…, m < n, могут быть разрешены относительно части переменных (не нарушая общности будем считать, что зависимыми переменными являются m Прочитать остальную часть записи »