Пример использования триггеров SQL для поддержания ссылочной целостности
Ниже написанные триггеры сделаны для базы данных, которая была опубликована ранее (см. Пример создания базы данных из нескольких таблиц на SQL). Хочется отметить то, что все названия триггеров являются русскоязычными. Также напомню, что база данных и триггеры созданы для MS SQL (проверялось).
Прочитать остальную часть записи »
Краткий обзор современных языков и систем моделирования
При моделировании динамических систем на ЭВМ в первую очередь необходимо представить их математические модели в виде программ. Следовательно, большое значение при реализации модели имеет правильный выбор языка моделирования.
Язык моделирования должен обеспечить:
1) удобство описания процесса функционирования системы,
2) удобство ввода исходных данных,
3) составление и варьирование структуры, параметров модели,
4) реализуемость как детерминированного, так и статистического моделирования.
Прочитать остальную часть записи »
Пример создания базы данных из нескольких таблиц на SQL
Пример создания базы данных на SQL в MS SQL. База данных состоит из пяти таблиц: Клиенты, Валюта, Вид_вклада, Вид_кредита, Вклады, Кредиты. Хочу отметить то, что все названия полей и названия таблиц написаны на русском языке.
Связи между таблицами:
1) таблица Клиенты связана с таблицами Вкладов и Кредитов по полю ид.
2) таблицы Вклады и Кредиты связаны соответственно с Вид_вклада и Вид_кредита по полю вид_вклада и вид_кредита соответственно.
3) таблицы Вид_вклада и Вид_кредита связаны с Валютой по полю ид_валюта.
Прочитать остальную часть записи »
Класс функций, сохраняющих константу
Определение: Функция f(x1, x2,…,xn) сохраняет константу a ⇔ f(a, a,…,a) = a, a∈{0,1}
Теорема: Класс функций, сохраняющих константу, замкнут относительно суперпозиции.
Доказательство: пусть функции f(x1, x2,…,xn), gi(x1, x2,…,xn), i=1..n сохраняют константу а, тогда их суперпозиция h = f(g1, g2,…,gn) тоже сохраняет константу а, ибо h(a, a,…,a) = f(g1(a, a,…,a), g2(a, a,…,a),…,gn(a, a,…,a)) = f(a, a,…,a) = a
Пулы соединения с базой данных
Поскольку речь идет о многопользовательских системах то, как мы уже говорили, на примере базы данных ORACLE – одно соединение экземпляра — 6мб и каждый следующий клиент – 500кб оперативной памяти для того чтобы хранить все сведения о соединении.
В последнее время разрабатывать СУБД для подключения 100 и более 1000 пользователей стало экономически невыгодно, пошли по другому пути — создания пулов соединения. Считается, что ресурсы потребляются только активными пользователями. Тот, кто « подключился, но пошел жевать пирожок и болтать о чем-то другом», т.е. активно соединение не использует, он переходит в пассив.
Прочитать остальную часть записи »
Выгорающие поглотители
Цель – выравнивание энерговыделения по R АЗ. Механизм – поглощение нейтронов – снижение Ф. Выполняются поглотители виде стержней, и вставляют их в АЗ при загрузке топлива. Не меняют свое положение в течение работы реактора.
Требования:
• Концентрация материала выгорающего поглотителя в конце компании реактора должна стремиться к нулю.
• Сечение захвата тепловых нейтронов велико.
Прочитать остальную часть записи »
Шаровые барабанные мельницы (ШБМ)
ШБМ имеет цилиндрический стальной корпус (барабан), который покрыт внутри броневыми плитами. Броневое покрытие чаще всего волнистое, реже используется каблучковая броня или броня с карманами (они более дорогие, но позволяют сделать мельницу компактнее). Барабан заполнен стальными шарами диаметром 50 мм и приводится во вращение через венцовое колесо, соединенное с редуктором. Мельница опирается на подшипники, расположенные в цапфах. Некоторые типы ШВМ опираются на размещенные внизу катки (вместо подшипников). Топливо и СА поступают в мельницу через входной патрубо, а готовая пыль выносится СА к сепаратору через патрубок. В пылесистемах ШБМ чаще всего бывает горячий воздух.
Прочитать остальную часть записи »
Пакеты прикладных программ
Основу многих современных систем моделирования (как и САПР) составляют пакеты прикладных программ (ППП). Комплексные программные системы могут объединять несколько ППП.
Пакеты прикладных программ могут быть:
• объектно-зависимыми, проблемно-ориентированными на определенную предметную область;
• объектно-независимыми, методоориентированными (инвариантными), т.е. могут использоваться при моделировании и решении задач из различных предметных областей.
Применение таких методоориентированных ППП часто менее эффективно:
• в них не учитывается специфика задач конкретной предметной области;
• требуется достаточно высокая математическая подготовка пользователя, так как при использовании объектно-независимых ППП необходима специальная предварительная подготовка задачи в соответствии с особенностями применяемого метода.
Прочитать остальную часть записи »
Лемма о нелинейной функции
Лемма о нелинейной функции.
Суперпозицией нелинейной функции, отрицания и константы 1 можно получить конъюнкцию.
Доказательство:
Пусть f(x1,…, xn ) — нелинейная функция, тогда полином Жигалкина для нее содержит слагаемое, в котором присутствует произведение каких-то переменных xi*xj. Пусть для простоты это будет произведение х1х2. Произведя группировку слагаемых в полиноме Жегалкина для f относительно x1х2, х1, х2, функцию f представим в виде f(x1,…, xn)=x1*x2*h0(x3,..,xn)+ {собрали все слагаемые с x1*x2 и вынесли x1*x2 за скобки. В скобках осталась сумма h0(x3,…,xn), в которой переменных x1, x2 нет} + x1*h1(x3,…, xn) + x2*h2(x3,…, xn) + h3(x3,…, xn)
Прочитать остальную часть записи »
Архитектура ODBC, JDBC, OCI, OLE DB и ADO
ODBC
Допустим, есть клиент, написанный к примеру на Visual C, есть база данных (ORACLE, MS SQL) и целая куча разных Desktops БД (Access, dBase, Paradox, Excel и т.д.). Как же происходит взаимодействие? Прежде всего, в системе устанавливается Microsoft Driver Manager (odbc32.dll). Эта dll-ка взаимодействует иногда с odbcint.ini и odbc.ini. Для работы с этой dll-кой есть администратор, который позволяет подключать драйверы (то что мы видим в панели управления).
Прочитать остальную часть записи »
Метод Четаева построения функции Ляпунова (второй метод Ляпунова)
Для того, чтобы применять приведенные выше теоремы об устойчивости, необходимо каким-то образом найти или построить функцию Ляпунова V.
Н.Г.Четаев предложил способ построения функции Ляпунова V в виде связки интегралов уравнений движения.
Определение 3.6. Функция V = V(x) называется первым интегралом уравнений движения (3.5.1)
Прочитать остальную часть записи »
Глубина выгорания топлива и компания реактора и топлива
Глубина выгорания
qвыг = Δmu/mu
Δmu — количество U, которое сгорело в реакторе,
mu — количество U, которое было загружено
Δmu = ТTt, MBT×сут, qвыг = NT×t/mU, MBD×сут/m=г/м
Прочитать остальную часть записи »
Общие сведения о процессе размола, угольной пыли и ее свойствах
Процесс размола дисперсных материалов хорошо описывается законом Риттингера (удельный расход электроэнергии на размол прямопропорционален величине вновь образующейся поверхности.
Эразм = A×Fобр
• Эразм, кВт×ч/т — энергия размола
• Fобр, м2 — вновь образующаяся поверхность
• A, кВт×ч/т×м2 — коэффициент, учитывающий твердость материала и совершенство процесса размола
Прочитать остальную часть записи »
Реализация непроцедурных систем программирования
Реализация НСП может быть достигнута лишь за счет их предметной (проблемной) ориентации, позволяющей построить в памяти компьютера описание модели предметной области (МПО).
Модель предметной области должна содержать множество (словарь) категорий (идентификаторов объектов), используемых в данной предметной области. Из сказанного следует, что НСП должна содержать терминологический словарь предметной области, a R(x) получается с помощью законов, известных в данный момент в предметной
области.
Прочитать остальную часть записи »
Многочлен Жигалкина
Определение: Многочлен Жигалкина в поле F есть выражение ∑(i1,..in)∈Ex1i1x2i2..xnin.
Где xi = {x при i=1, 1 при i=0}.
Теорема Жигалкина: Всякую функцию алгебры логики можно представить единственным полиномом Жигалкина.
Прочитать остальную часть записи »
Стандартизация доступа к базам данных
Шлюзы и ORB
Архитектура клиент серверной системы подразумевает не только распределение вычислительных ресурсов, но и разделение функций между ресурсами. Когда мы приступаем к разработке клиент серверной системы, часто приходится учитывать тот случай, что у клиентов (кто заказывает приложение) могут оказаться уже большие объемы каких-то данных, хранящиеся в каких-то СУБД. Часто бывает так, что это достаточно старые информационные системы, которые не так-то просто преобразовать к клиент-серверной системе.
Прочитать остальную часть записи »
Теорема об устойчивости. Теорема об неустойчивости
Теорема 1. (теорема Ляпунова об устойчивости) Если для уравнений возмущенного движения (1.18) можно найти знакоопределенную функцию V, производная V• которой в силу этих уравнений была бы или знакопостоянной функцией противоположного знака с V, или тождественно равной нулю, то невозмущенное движение x=0 устойчиво относительно величин x1, x2, …, xN.
Прочитать остальную часть записи »
Реактивность реактора
Состояние реактора описывает коэффициент эффективного размножения. Но когда реактор находится не в критическом состоянии, то его удобнее описывать коэффициентом реактивности:
ρ = (kэф-1)/kэф ≈ kэф — 1
Реактивность удобна для описания процессов в АЗ. Когда процессы приводят к повышению kэф, то говорят, что вносится положительная реактивность ρ>0. Когда kэф уменьшается – имеет место отрицательная реактивность. Реактивность измеряется в относительных единицах или процентах. β — доля запаздывающих нейтронов, образующихся в процессе деления – граница управляемости реактора. Отравление приводит к отрицательной реактивности.
Прочитать остальную часть записи »
Общий вывод по организации (экономика)
По активу: при анализе сравнительного аналитического баланса отмечается, что оборот хозяйственных средств (стоимость имущества) на конец года уменьшился на 10 459 тыс. рублей, что составляет 28,4% к началу года. В основном уменьшение оборота произошло за счет уменьшения оборотных активов на 9 701 тыс. рублей (43,3%). Увеличена стоимость основных средств на 1 942 тыс. рублей (17,4%), это произошло за счет того, что было завершено строительство, и объект был введен в эксплуатацию.
Прочитать остальную часть записи »
Класс линейных функций и его замкнутость относительно суперпозиции
Определение: Арифметические функции в алгебре логики есть сложение и умножение по модулю 2.
Следующие свойства математических операций проверяются непосредственно.
1) x+(y+z) = (x+y)+z
2) x+y=y+x
3) x+0=x
4) x+(-x) = 0
5) x(yz) = (xy)z
6) xy = yx
7) x*1 =x
8) x*x-1 =1, x≠0
9) x(y+z) = xy+xz
10) x+x=0
11) x*x =x (идемпотентность)
Прочитать остальную часть записи »
Принцип поточности организации процесса горения
Естественной основой всякого установившегося процесса горения является поточная схема его организации. Начиная со стадии предварительной подготовки топлива и кончая эвакуацией продуктов сгорания из объема топки.
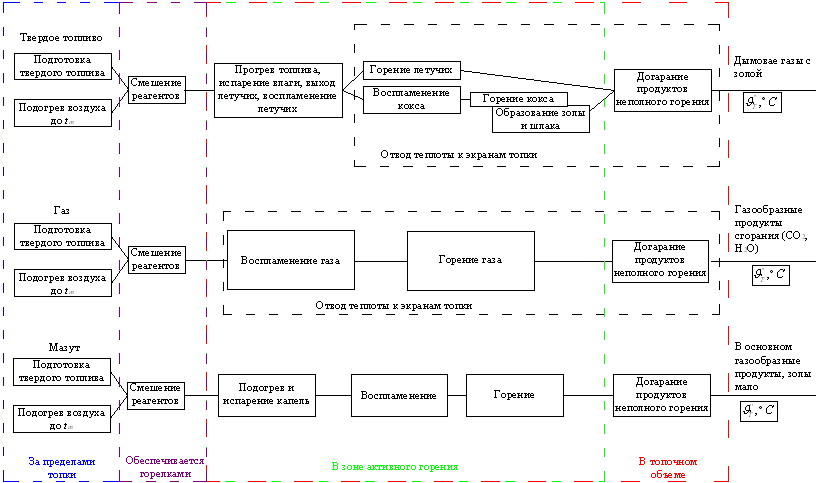
Прочитать остальную часть записи »
Основные принципы клиент серверных систем
Здесь предполагается, что клиент есть одна машина, а сервер – другая машина.
Основные принципы клиент серверных систем:
1. Сохранение автономности сервера. Т.е. клиенты не должны ограничивать доступность сервера и нарушать его целостность.
Прочитать остальную часть записи »
Функциональные блоки систем имитационного моделирования и их программная реализация
Исходя из особенностей имитационного моделирования, наиболее рационально строить модель по блочному принципу. Основные группы функциональных блоков были упомянуты ранее.
Каждый блок выполняет определенную законченную функцию, поэтому он достаточно автономен и должен иметь минимальное количество связей с другими блоками. Разумеется, что каждому такому блоку соответствует своя, как правило, типовая математическая модель. Например, это могут быть модели типовых динамических звеньев, модели генерации сигналов, схемы вероятностных и конечных автоматов, схемы массового обслуживания, которые достаточно точно описывают основные особенности реальных процессов.
Прочитать остальную часть записи »
Устойчивость регенерирующих процессов
В этом посте будет изучаться устойчивость, сформулированная в терминах маргинальных распределений, характеризующих регенерирующие процессы. За определение устойчивости можно взять определение 1.1, если в качестве h(zt, zt*) выбрать какое-либо расстояние, зависящее лишь от маргинальных распределений величин zt и zt* (ниже для определенности будет рассматриваться только расстояние Дадли d, «порождающее» слабую сходимость), а под μ(α, α*) понимать соответствующим образом введенную меру отклонения возмущенных параметров от невозмущенных, также определяемую маргинальными характеристиками процессов zt и zt*. Более подробная «расшифровка» μ(α, α*) будет дана ниже.
Прочитать остальную часть записи »
Некоторые подходы к решению задач невыпуклого программирования
Рассмотрим задачу нелинейного программирования следующего
вида:
min xn, где D = {x|gi(x) ≥ 0, i = 1,2, …, m}. (7.97)
Относительно допустимой области D предположим, что она является односвязным замкнутым множеством. В отличие от задачи выпуклого программирования допустим, что множество D может не удовлетворять условию выпуклости. В этом случае задача (7.97) является задачей невыпуклого программирования и может иметь несколько локальных минимумов.
Прочитать остальную часть записи »
Устойчивость на всей оси времени
Ранее рассматривалась задача анализа устойчивости предельных режимов у изучаемых процессов. В соответствии с этим в расчет принимались либо меры отклонения финальных распределений (слабая устойчивость в пределе), либо меры отклонения, усредненные по времени (устойчивость в среднем по времени). Если априори известно, что рассматриваемая система функционирует «достаточно долго», то анализ устойчивости в смысле приведенных определений оправдан, практически важен и может дать существенную информацию относительно ее поведения. Однако такая ситуация встречается далеко не всегда. Часто длина отрезка функционирования заранее не определяется и неизвестна. Поэтому (и наряду с этим) неизвестно также «время вхождения» системы в установившийся режим. Не исключены и случаи отсутствия «установившегося режима». Эти обстоятельства ведут к необходимости изучения устойчивости, которая является равномерной относительно времени, а также скорости сходимости к финальным распределениям.
Прочитать остальную часть записи »
Алгоритм, реализующий метод внутренних точек
Алгоритм, реализующий метод внутренних точек, можно представить в виде следующей последовательности действий.
1. Из решения вспомогательной задачи находится начальное приближение х°, принадлежащее множеству внутренних точек D0, и принимается хr0 = х°. (Если априори точка x°∈D0 известна, то этот этап опускается.)
Прочитать остальную часть записи »
Примеры устойчивости предельных режимов
Во всех приводимых ниже примерах равномерная независимость процесса от начального состояния проверяется путем не слишком сложного построения конкретных множеств ВN для которых выполнены свойства (2.24) и (2.25).
Пример 1. Многолинейная система обслуживания с ожиданием. Рассмотрим процесс zt введенный в примере 1.2.3:
zt+1 = R(zt + ηte — θtI)+. (1)
Преобразование задачи нелинейного программирования при помощи функций штрафов в последовательность задач безусловной оптимизации
Рассмотрим класс алгоритмов, которые позволяют решение задачи нелинейного программирования свести к решению последовательности задач безусловной оптимизации.
В общем виде такое преобразование осуществляется при помощи специальным образом сконструированной функции, называемой штрафной функцией (функцией нагружения и т. д.):
Ф(х, cr) = Q(x) + R(х, cr) = Q (X) + сrψ(х). (7.77)
Постановка задачи устойчивости предельных режимов
Рассмотрим однородный марковский процесс zt, задаваемый рекуррентным соотношением вида (1.1.5), т. е.
zt+1 = F(zt, ξt), t≥0. (1)
Хотя результаты, приводимые в этой и следующей главах, имеют более общий характер, все же всюду будет считаться, что zt задается именно соотношением вида (1). Будем смотреть на это соотношение как на преобразование «управляющей» последовательности {ξt} и начального состояния z0 в последовательность {zt} (удобно начальное состояние z0 считать, с одной стороны, управляющим параметром, а с другой — управляемым).
Прочитать остальную часть записи »