Задача минимизации одномерной унимодальной функции Q(х), определенной на интервале [а, b], связана с поиском оптимального решения х*:

Q(x*)= min Q(x). (3.1)

Из свойства унимодальности функции Q (х) следует, что с возрастанием переменной х функция Q (х) строго убывает при х ≤ х* и строго возрастает при х ≥ х*, т. е. унимодальная функция не должна иметь горизонтальных участков («плато»), хотя может быть не дифференцируемой, разрывной, неопределенной в некоторых точках и т. д. В начале поиска положение точки х* на интервале [а, b] неизвестно. Путем проведения в точках рассматриваемого интервала N испытаний требуется локализовать оптимальное решение х* в интервале [a_N, b_N] меньшей длины, чем исходный. При этом предполагается, что каждое испытание, связанное с вычислением значения функции Q (х), может быть выполнено без ошибки, либо последняя настолько мала, что ею можно пренебречь. В дальнейшем интервал [a_N, b_N] будем называть апостериорным интервалом неопределенности в отличие от исходного интервала [а, b], называемого априорным интервалом неопределенности.

Методы оптимизации, основанные на рассмотренном свойстве унимодальности минимизируемой функции, называются методами сокращения интервала неопределенности. Основная идея этих методов заключается в том, что на каждом k-м шаге поиска путем исключения тех подынтервалов, в которых в силу унимодальности функции Q (х) точка х* не содержится, определяется текущий интервал неопределенности [а_k+1, b_k+1], удовлетворяющий системе неравенств:

a_k ≤ a_k+1 ≤ b_k+1 ≤ b_k (3-2)
и a_k ≤ a_k+1 или b_k+1 < b_k.

Длина l текущего интервала неопределенности [а_k+1, b_k+1] как видно из рис. 3.1, зависит от расположения в интервале |a_k,b_k| точек испытаний x₁^k, x₂^k, выбор которых определяется конкретным методом
поиска Fⁱ. Тогда наилучший метод F* из некоторой совокупности рассматриваемых методов сокращения интервала неопределенности А_F должен обеспечивать минимальное значение длины апостериорного интервала неопределенности после проведения N испытаний для самой «наихудшей» функции Q (х) из класса унимодальных функций К_Q

l(F*)= min max |b_N — a_N| (3.3)

Такой подход к выбору наилучшего метода F* минимизации одномерных унимодальных функций Q (х), определенных на интервале [а, b], называется минимаксным подходом (принципом гарантированного результата).

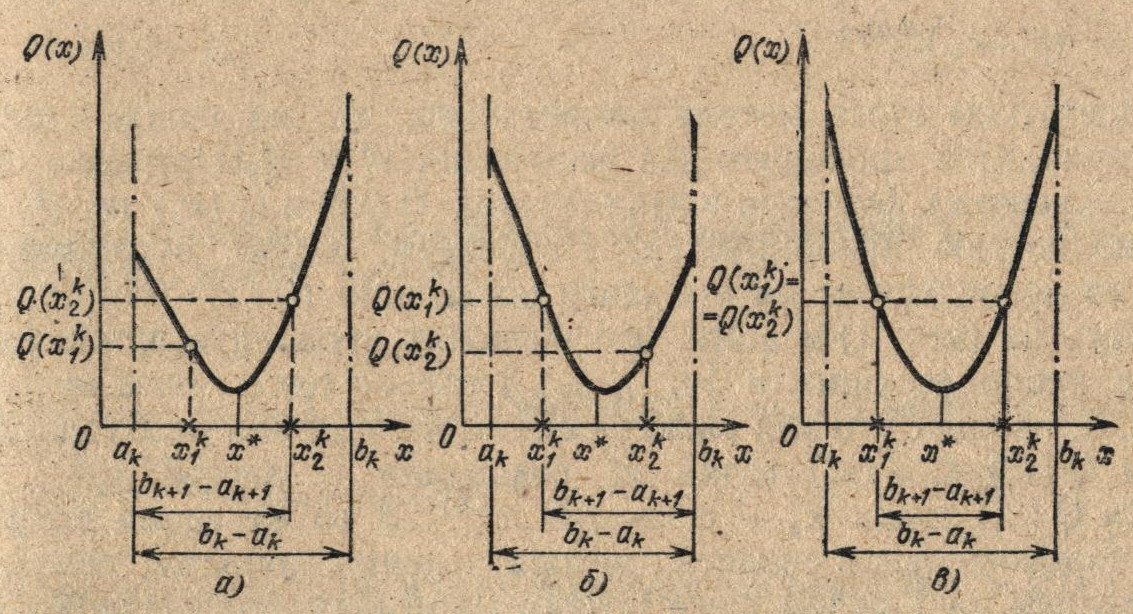
Рис. 3.1. Уменьшение априорного интервала неопределенности [a_k, b_k] путем проведения двух испытаний в точках x₁^k, x₂^k

Согласно экстремальной задаче (3.3) на каждом k-м шаге поиска точки испытаний x₁^k, x₂^k должны выбираться таким образом, чтобы наибольшая длина интервала неопределенности [a_k+1, b_k+1] была как можно меньше:

min max {x₂^k — a_k, b_k — x₁^k}

при условии, что

a_k ≤ x₁^k ≤ x₂^k ≤ b_k

Решением задачи (3.4) является пара точек, расположенных симметрично относительно середины интервала неопределенности [a_k, b_k]:

x₁^k = ((a_k + b_k) — δ)/2, x₂^k = ((a_k + b_k) + δ)/2. (3.5)

Здесь δ > 0 — минимально допустимое различие между точками испытаний x₁^k и x₂^k, при котором возможно точно определить знак разности [Q (x₁^k) — Q (x₂^k)], т. е. параметр δ имеет такое значение, что если |x₁^k — x₂^k| > δ, то Q (x₁^k) = Q (x₂^k) только в том случае, когда x₁^k и x₂^k лежат по разные стороны от оптимального решения х*.

Метод поиска F¹, реализующий процедуру выбора точек испытаний по формуле (3.5), называется методом деления пополам (методом последовательного дихотомичевкого поиска). Согласно этому методу на каждом шаге поиска пара испытаний, разнесенных между собой на величину δ, проводится в середине текущего интервала неопределенности |a_k, b_k|. По значениям функции Q (х), полученным в этих точках, одна половина исследуемого интервала в силу унимодальности минимизируемой функции исключается из дальнейшего рассмотрения. В середине оставшейся части интервала неопределенности вновь делается пара испытаний и т. д. После проведения (N/2) пар испытаний для длины апостериорного интервала неопределенности получаем выражение:

l_N (F¹) = (b — δ)/2^N/2. (3.6)

Недостатком этого метода является то, что на каждом шаге поиска приходится проводить два испытания x₁^k и x₂^k. Причем информация о значениях функции в этих точках Q (x₁^k) и Q (x₂^k) на (k + 1)-м
шаге полностью игнорируется. Потребуем, чтобы информация об одном из проведенных на k-ш шаге испытаний (Q (x₁^k) или Q (x₂^k)) сохранялась на (k + 1)-м шаге, что позволит проводить в текущем интервале неопределенности [a_k+1, b_k+1 только одно новое испытание.

Из рис. 3.1 видно, что для выполнения этого условия необходимо, чтобы при Q (x₁^k) < Q (x₂^k) точка x₁^k совпадала с точкой x₂^k+1, а при
Q (x₁^k) > Q (x₂^k) точка x₂^k — с точкой x₁^k+1 то же время потребуем, чтобы положительное свойство метода деления пополам, связанное Q обеспечением на каждом шаге поиска минимального значения длины наибольшего возможного интервала неопределенности, сохранялось.

Из (3.5) следует, что для выполнения этого требования необходимо выбирать точки x₁^k, x₂^k на интервале [a_k, b_k] эквидистантно от обоих его
концов, соответственно в подынтервалах [a_k, (a_k + b_k)/2] и [(a_k + b_k)/2, b_k]:

x₁^k — a_k = b_k — x₂^k;

a_k ≤ x₁^k ≤ (a_k + b_k)/2; (3.7)

(а_k + b_k)/2 ≤ x₂^k ≤ b_k.

Нетрудно видеть, что условия (3.7) выполняются, если точки испытаний x₁^k, x₂^k∈[а_k, b_k] вычисляются по формулам:

x₁^k = а_k + t_k (b_k — a_k), (3.8)

x₂^k = a_k + (1 — t_k)(b_k — a_k). (3.9)

где

0 ≤ t_k ≤ 1/2. (3.10)

При этом длина интервала неопределенности [a_k+1, b_k+1] не зависит от вида функции Q (х) и имеет следующую величину:

b_k+1 — a_k+1 = x₂^k — a_k = b_k — x₁^k = (1 — t_k) (b_k — a_k). (3.11)

Комментарии запрещены.