Архив рубрики «Теория устойчивости»
Бифуркация равновесий
Потенциальная энергия П механической системы, как правило, зависит не только от обобщенных координат q, но и от таких параметров системы, как масса, длина, жесткость пружины и т.д.
При изменении параметров системы поведение системы в окрестности положения равновесия также может изменяться – устойчивое положение равновесия может стать неустойчивым и, наоборот, неустойчивое положение равновесия может стать устойчивым.
Прочитать остальную часть записи »
Устойчивость абсолютного равновесия
Рассмотрим движение механической системы, имеющей n степеней свободы, на которую наложены голономные удерживающие связи.
Уравнения движения системы запишем в форме уравнений Лагранжа II рода
d/dt ∂T/∂q• — ∂T/∂q = — ∂П/∂q + QН. (4.1)
Устойчивость установившихся движений
Рассмотрим движение механической системы, имеющей n степеней свободы, на которую наложены голономные удерживающие связи.
Уравнения движения системы запишем в форме уравнений Лагранжа II рода
d/dt (∂T/∂q•)T — (∂T/∂q)T = — (∂П/∂q)T + QН. (4.1)
Правила построения функции Ляпунова в виде связки интегралов методом Четаева
Функция Ляпунова для исследования устойчивости невозмущенного движения строится в
виде суммы первых интегралов уравнений возмущенного движения (3.5.1)
V = λ1V1 + λ2V2 + …+ λkVk + μ1V12 + μ2V22 + …+ μkVk2 = const, (3.16)
Метод Четаева построения функции Ляпунова (второй метод Ляпунова)
Для того, чтобы применять приведенные выше теоремы об устойчивости, необходимо каким-то образом найти или построить функцию Ляпунова V.
Н.Г.Четаев предложил способ построения функции Ляпунова V в виде связки интегралов уравнений движения.
Определение 3.6. Функция V = V(x) называется первым интегралом уравнений движения (3.5.1)
Прочитать остальную часть записи »
Теорема об устойчивости. Теорема об неустойчивости
Теорема 1. (теорема Ляпунова об устойчивости) Если для уравнений возмущенного движения (1.18) можно найти знакоопределенную функцию V, производная V• которой в силу этих уравнений была бы или знакопостоянной функцией противоположного знака с V, или тождественно равной нулю, то невозмущенное движение x=0 устойчиво относительно величин x1, x2, …, xN.
Прочитать остальную часть записи »
Геометрическая интерпретация уравнений возмущенного движения
Пусть уравнения возмущенного движения имеют вид
dx/dt = F(x), F(0) = 0, x(t0) = x0. (3.5.1)
Определение 5. Производной dV/dt функции V(x) = V(x1, x2, …, xN) в силу уравнений возмущенного движения (1.18) называется ее полная производная по времени, вычисленная в предположении, что величины x1, x2, …, xN удовлетворяют уравнениям (1.18), т.е.
Прочитать остальную часть записи »
Геометрические свойства знакоопределенной функции Ляпунова
Геометрические свойства знакоопределенной функции Ляпунова V(x)
1. Если функция V(x) знакоопределенная, то поверхность V(x1, …, xn)=c=const в пространстве (x1, …, xn) является замкнутой поверхностью (рис.3.1).
Прочитать остальную часть записи »
Определения функции Ляпунова и критерий Сильвестра
Задачи 1. Найти точки экстремума (критические точки) для функций:
1) V5(x1, x2) = x1 — 3 x2 + x1 x2,
2) V6(x1, x2) = x13 — x22 — 2x12,
3) V7(x1, x2) = 3x12 + x22 — x13,
4) V8(x1, x2) = x13 +4 x23+ x24.
Прочитать остальную часть записи »
Функции Ляпунова. Критерий Сильвестра
Рассмотрим однозначную функцию V(x) = V(x1, …, xN), определенную в области
||x (t)|| < ε, (3.1)
обращающуюся в нуль V(0) = 0 при x = 0 и обладающую непрерывными первыми частными Прочитать остальную часть записи »
Второй метод Ляпунова. Введение
Задача об устойчивости нулевого решения x=0 системы дифференциальных уравнений
dx/dt = F(x), F(0) = 0, x (t0) = x0. (3.0)
может быть решена без особых трудностей, если эта система может быть проинтегрирована и в явном виде получены выражения для решения x = x(t, x0) системы (3.0) как функции времени и начальных условий.
Прочитать остальную часть записи »
Примеры критериев Рауса-Гурвица и Льенара-Шипара
Пример 1. Исследовать устойчивость установившегося движения равномерно вращающегося ротора на линейно упругом валу в случае идеального двигателя (неограниченной мощности), который обеспечивает в любой момент времени постоянную
угловую скорость вращения ротора ω = const.
Прочитать остальную часть записи »
Критерии Рауса-Гурвица и Льенара-Шипара
Существуют различные критерии определения знака действительных частей корней характеристического уравнения (2.3). Наибольшее распространение получил критерий Рауса-Гурвица, который дает необходимые и достаточные условия отрицательности действительных частей всех корней характеристического уравнения системы.
Прочитать остальную часть записи »
Примеры устойчивости по первому приближению
Пример 1. Найти положения равновесия нелинейной системы и исследовать их устойчивость с помощью теорем Ляпунова об устойчивости по первому приближению
x• = a x — c x y, c≠0
y• = — by + d x y, d≠0.
Показать, что в зависимости от знаков параметров a, b выводы об устойчивости различные.
Прочитать остальную часть записи »
Теоремы об устойчивости по первому приближению
А.М. Ляпунов доказал ряд теорем, согласно которым об устойчивости нулевого решения x=0 нелинейной системы (2.1) можно судить по устойчивости ее линейной части
(2.2). Приведем некоторые из них для случая постоянной матрицы A1 = const.
Замечание 1. Если элементы матрицы A1 = A1 (t) зависят от времени, то уравнения первого приближения (2.2) являются линейными нестационарными дифференциальными уравнениями. Технология исследования устойчивости нулевого решения в данном случае является более сложной и отличается от той, которая представлена ниже.
Прочитать остальную часть записи »
Уравнения первого приближению
Выделим в правой части уравнений возмущенного движения (1.18) линейные слагаемые и запишем эти уравнения в виде
dx/dt= A1x + F2(x), x(t0) = x0. (2.1)
Здесь A1 — матрица размерности NxN, элементы которых определяются, линейными слагаемыми вектора правых частей F(x) уравнения (1.18), F2(x) — N-мерный вектор-столбец нелинейных слагаемых, причем F2(0) = 0.
Прочитать остальную часть записи »
Асимптотической устойчивости по Ляпунову. Неустойчивости по Ляпунову
Определение (асимптотической устойчивости по Ляпунову): Невозмущенное движение x = 0 системы (1.19) называется асимптотически устойчивым по Ляпунову относительно величин x, если
а) оно устойчиво
б) если существуют такое число Δ > 0, что для любых Прочитать остальную часть записи »
Уравнения возмущенного движения
Чтобы вывести уравнения возмущенного движения введем новые переменные, представляющие собой отклонения (или вариации) x1, x1•=x2 возмущенного движения q(t), q•(t) (1.5) от невозмущенного ξ(t), ξ•(t) (1.3), а именно:
q(t) = ξ(t) + x1, q•(t) = ξ•(t) + x1•. (1.15)
Прочитать остальную часть записи »
Особенности определения устойчивости по Ляпунову
Особенности определения устойчивости по Ляпунову
1. В основе определения устойчивости по Ляпунову лежит понятие числа, а не бесконечно малой величины.
Замечание. Это факт имеет большое практическое значение, поскольку по заданным величинам ε1, ε2, характеризующим отклонения возмущенного движения от невозмущенного в любой момент времени, можно найти другие числа δ1, δ2, характеризующие численные значения начальных возмущений, которые являются численно малыми, но конечными.
Прочитать остальную часть записи »
Неустойчивости по Ляпунову и асимптотическая устойчивость по Ляпунову
Определение (неустойчивости по Ляпунову) Невозмущенное движение qp = ξ(t), qp•=ξ•(t) системы (1.1) называется неустойчивым по Ляпунову относительно величин q, q•, если существуют числа ε10, ε20 > 0 такие, что для любых чисел δ1, δ2 > 0 существует решение q(t), q•(t) уравнений (1.1) и момент времени t1 > t0 такие, что,
Прочитать остальную часть записи »
Постановка задачи об устойчивости движения. Определение устойчивости по Ляпунову
Рассмотрим движение механической системы, имеющей n степеней свободы, на которую наложены голономные стационарные удерживающие связи. Уравнения движения системы можно записать в форме уравнений Лагранжа II рода
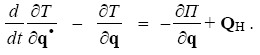 (1.1)
(1.1)Прочитать остальную часть записи »
Общие представления об устойчивости движения
Общие представления об устойчивости движения
Основы теории устойчивости движения были разработаны великим русским ученым А.М.Ляпуновым (1857 — 1918).
Разработка любого технического устройства (манипулятора, мобильного робота, спутника, гироскопической системы и т.д.) является сложной научно-технической проблемой. Поскольку на практике реализуются лишь устойчивые движения, то важнейшей задачей, которая возникает уже на этапе проектирования любой машины или механизма, является задача обеспечения устойчивости их движений.
Прочитать остальную часть записи »