Z — преобразование
26.07.2010 |Для описания и анализа дискретных систем, решения разностных и рекуррентных уравнений используется Z -преобразование.
Z-преобразование применяют к сигналу, квантованному по времени (к дискретным значениям непрерывного сигнала).
Z -преобразование определяется как сумма отрицательных степеней комплексной переменной z с помощью соотношения:
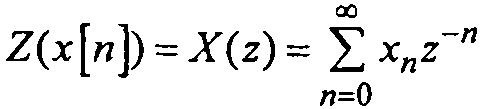(1.18)Таким образом, Z -преобразование представляет собой последовательность уменьшающихся степеней z, имеющих коэффициенты, равные амплитудам последовательных значений х[n]:
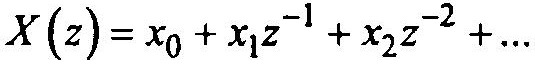
Так, для единичной ступенчатой функции u[n] = 1 (n = 0,1,2,..) имеем
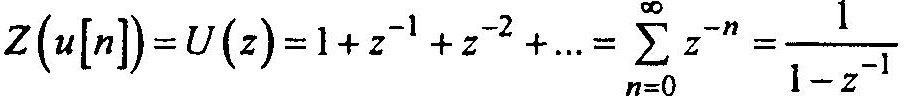
По аналогии с непрерывными сигналами отношение
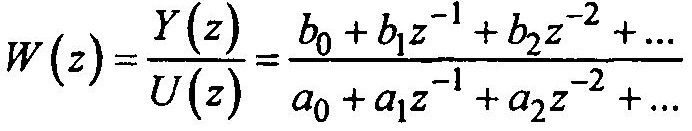
1.19
называют дискретной (импульсной) передаточной функцией. На основании (1.19) для частного случая можно записать
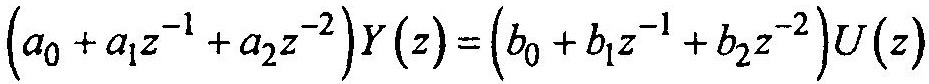
Умножение Z-преобразования функции на оператор z-1 соответствует задержке последовательности значений (импульсов) на один временной такт τ. Тогда из последнего выражения легко получить разностное уравнение
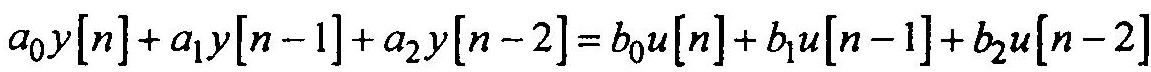
Отметим, что Z — преобразование можно представить и в следующей эквивалентной форме:
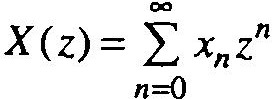
Если умножение на z-n означает задержку хn на n тактов, то умножение на zn означает опережение на n тактов. Но опережение сигнала на n тактов нельзя осуществить, а задержка сигнала осуществляется легко. Поэтому схемы моделирования сигналов в дискретной форме реализуются на элементах задержки.
Таким образом, с помощью операции Z -преобразования легко устанавливается соответствие между импульсными передаточными функциями (описывающими динамику дискретных систем в комплексной плоскости) и разностными уравнениями (описывающими поведение динамических систем во временной области).
