Модель узла связи как КЛП Гнеденко — Коваленко. Предварим разбор примера кратким описанием системы. Рассмотрим сеть связи, задаваемую некоторым графом (рис. 2).

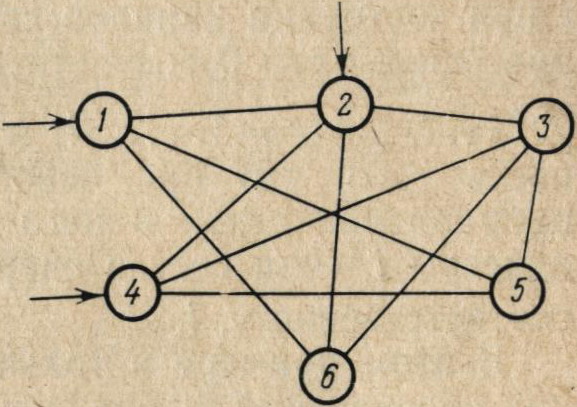
Рис. 2

Узлы графа соответствуют узлам связи, а дуги — направлениям связи. Система работает следующим образом. В не-которые моменты времени на отдельные узлы связи (на рис. 2 они отмечены номерами 1, 2, 4) извне поступают сообщения, подлежащие передаче по сети. Сообщения характеризуются, вообще говоря, рядом признаков: адресом, приоритетом, предельным сроком нахождения в сети и т. д. Узел связи в соответствии с алгоритмом своей работы либо посылает это сообщение в одно из примыкающих к нему направлений связи, либо запоминает его и хранит до ближайшего момента времени, когда появится возможность послать его в сеть. Указанные альтернативы определяются загрузкой сети, наличием свободных каналов связи и пр. Таким образом, в узле связи могут образовываться очереди из сообщений, ждущих своей отправки.

Рассмотрим узел связи вместе с выходящими из него направлениями связи. Пусть работа узла определяется алгоритмом A. Величины, которые характеризуют этот алгоритм, будем отмечать буквой A. Предположим, что рассматриваемый узел связи может посылать сообщения в R направлений связи, R ≥ 1, причем r-е направление (1 ≤ r ≤ R) состоит из m_r каналов связи. По каждому из каналов связи одновременно может передаваться не более одного сообщения.

Обозначим М = ∑ m_r. Каждое
сообщение, поступающее на рассматриваемый узел, характеризуется приоритетом π (π=1, …, П) и адресом i (i= 1, …, N). Будем считать, что узел связи работает «мгновенно». Тогда сообщения, предназначенные для этого узла, можно не принимать во внимание, т. е. можно считать данный узел полностью «транзитным».

Предположим, что сообщения не теряются, и имеется неограниченное число мест для ожидания ими дальнейшей передачи.

Обозначим через v* = (v⁽¹⁾, …, v^(π)) состав очереди из сообщений, хранимых в узле связи, где

v^(π) = (v^(π)(1), …, v^(π)(N)),

v^(π)(i) — число сообщений типа π с адресом i, хранимых в рассматриваемом узле. Каналы передачи сообщений в каждом направлении загружаются сразу же по мере их освобождения (если есть сообщения, которые могут быть по ним переданы).

Предположим для простоты, что характеристики всех каналов связи идентичны. Кроме того, предположим, что все каналы абсолютно надежны.

Введем следующие обозначения:

F_π,i(x) (π = 1, …, П; i = 1, …, N) — функция распределения времени передачи сообщения типа π с адресом i по каналу связи, входящему в r-е направление;

η^(r)(j) (j=1, …, m_r, r=1, …, R) — время, оставшееся до освобождения j-го канала в r-м направлении;

ξ^{(π ,i)}(j) (j = 1, …, v_π(i)) — время, необходимое для передачи j-го сообщения типа π с адресом i, находящегося в памяти;

l^(r) — число сообщений, передающихся по каналам в r-м направлении связи, l = (l⁽¹⁾, …, l^(R));

v= (v*, l); Здесь, как и в предыдущем примере, v является не числом, а целочисленным вектором.

p_r(i, π, l, A) (r = 0, 1, …, R; π = 1, …, П; i = 1, …, N) — вероятность того, что поступившее сообщение типа π с адресом i при состоянии каналов связи l будет послано в r-е направление связи (r = 0 соответствует посылке сообщения в очередь);

q_r^{i, π}(v*, l, A) (r = 1, …, R; π = 1, …, П; i= 1, …, N) —вероятность того, что при освобождении одного из каналов в r-м направлении связи в него будет послано сообщение типа π с адресом i, если состав очереди и загрузка каналов связи были соответственно v*, l.

В этом примере и только во избежание еще более громоздких обозначений будем пренебрегать возможностью одновременного окончания процесса передачи различных сообщений. Это заведомо можно сделать, если у функций распределения F_{π, i}, существуют плотности. Вероятности р и q задают порядок передачи сообщений, определяются алгоритмом A работы узла и удовлетворяют ряду естественных ограничений:

∑ p_r(i, π, l, A) = 1; p_r(i, π, l, A) = 0, если l^(r) = m_r;

q_r^{(i, π)}(v*, l, A) = 0, если l^(r) = m_r или v_i^π = 0;

∑q_r^{(i, π)}(v*, l, A) ≤ 1.

Предположим, что если узел связи с выходящими из него направлениями связи находится в состоянии v, то сообщения типа π с адресом i поступают на него в соответствии с пуассоновским потоком, имеющим параметр Λ_{π, i} (v). Это предположение представляется оправданным при большом числе каналов, подходящих к узлам связи, и широко используется. Рассмотрим процесс z_t, состояния которого имеют вид z = (v, z^v), где z^v = (z^v(0), z^v(1), …, z^v(R)),

Положим |v| = |v*| + ∑l^(r), v^v = (v^v (0), v^v (1), …, v^v (R)), где

|v*| = ∑ ∑ v^(π)(i),

v^v(0)—нулевой вектор размерности |v*|,
v^v(r)—вектор размерности l^(r), состоящий из 1 ≤ r ≤ R,

λ(v) = ∑Λ_{π, i}(v).

Пусть v = (v⁽¹⁾, …, v^(π), l). Положим

p_{v, μ} = 1/λ(v) Λ_{π, i}(v) p_r (i, π, l, A)

для

|μ| = |v| + 1.

Для состояний μ отличных от выписанных выше, вероятности p_{v, μ} положим равными 0. Для этой же пары (v, μ) распределение H_{μ, v}, очевидно, представляет собой распределение одной случайной величины и имеет вид F_{π, i}(х).

Вероятности q_{v, μ}(j₁, …, j_m) в силу сделанного допущения следует определять только для m= 1. Именно, q_{v, μ}(j) = q_r^{π, i}(v*, l, A)
если |v*| + ∑l^(k) < j ≤ |v*| + ∑l^(k), 1 ≤ r ≤ R, для

μ = (v⁽¹⁾, …,v^(π)(i) — 1, …, v^(π)(N)], …, v^(П)(i), l)
и
q_{v, μ}(j) = 1 — ∑q_r^{π, i}(v*, l, A)
если
|v*| + ∑l^(k) < j ≤ |v*| + ∑l^(k), 1 ≤ r ≤ R.

Тогда процесс z_t, определяемый параметрами v^v, λ(v), q_{v, μ}(j) и H_{v, μ}, является КЛП Гнеденко — Коваленко.

Комментарии запрещены.