Без потери общности предположим, что решается задача минимизации унимодальной функции Q (х), определенной на единичном интервале [0, 1], во внутренней точке ξ которого имеется информация о численном значении функции Q (ξ). В этом случае применение процедур сокращения интервала неопределенности позволяет получить после проведения N испытаний апостериорный интервал неопределенности [a_N, b_N], длина которого определяется следующим выражением:

l_N(ξ) = b_N — a_N = max ((1-ξ)/u_N, ξ/u_N-1), 0 ≤ ξ ≤ 1/2; (3.61)

l_N(ξ) = b_N — a_N = max ((1-ξ)/u_N-1, ξ/u_N), 1/2 < ξ ≤ 1; (3.62)

Соотношение (3.62) получается из (3.61) по симметрии:

l_N(1-ξ) = l_N(ξ) для 1/2 ≤ ξ ≤ 1.

В связи о этим докажем справедливость только выражения (3.61).

При N = 1 испытание в точке

ξ₁ = {1/2, если ξ ≠ 1/2;
1/2 + δ — в противном случае}

позволяет получить апостериорный интервал неопределенности

l₁ (ξ) = max (1 — ξ, ξ)

что и подтверждает справедливость (3 61).

Пусть соотношение (3.61) имеет место при (N — 1)-м числе испытаний Докажем его справедливость для N испытаний, предположив, что

0 ≤ ξ ≤ u_N-1/u_N+1.

Покажем, что в атом случае

l_N(ξ) ≥ (1 — ξ)/u_N. (3.63)

Пусть на отрезке [ξ, 1] задана произвольная унимодальная функция Q (x). Доопределим ее следующим образом:

Q*(x) = Q(ξ) — x + ξ при 0 < x ≤ ξ Q*(x) = Q(x) при ξ ≤ x ≤ 1

Нетрудно видеть, что построенная функция Q*(х) является унимодальной и ее минимум совпадает с точкой минимума функции Q (х). Допустим от противного, что неравенство (3.63) не выполняется, т. е. для функции Q (х), определенной на отрезке [0, 1], существует процедура поиска F, которая позволяет получить апостериорный интервал неопределенности

l_N(F) < (1 - ξ)/u_N

С другой стороны, для унимодальной функции Q*(x), как было показано ранее, наилучшим является метод Фибоначчи, который гарантирует получение после N испытаний наименьшего допустимого апостериорного интервала неопределенности не меньше чем 1/u_N, что больше чем (1 — ξ)/u_N. Следовательно, мы пришли к противоречию, что и доказывает справедливость неравенства (3.63). Установим теперь справедливость противоположного неравенства

l_N(ξ) ≤ (1 — ξ)/u_N

Первое испытание будем проводить по методу Фибоначчи, предположив, что а = ξ, b = 1 и число испытаний равно (N — 1), в точке

ξ₁ = ξ + (1 — ξ)/u_N-2/u_N. (3.65)

Если Q (ξ₁) ≤ Q (ξ), то х*∈[ξ, 1] и так как ξ₁ выбрано по, методу Фибоначчи, то после N испытаний получим

l_N(ξ) = (1 — ξ)/u_N.

Если Q(ξ₁) > Q(ξ), то необходимо рассмотреть следующие три случая.

Случай 1.

ξ/ξ₁ ≤ u_N-2/u_N

Точка минимума х* принадлежит интервалу [0, ξ₁], в котором необходимо провести (N — 1) испытание. В связи с тем, что оценки (3.60) справедливы для (N — 1)-го испытания, можем записать, что

l_N(ξ) = ξ₁l_N-1(ξ) = ξ₁(1 — ξ)/u_N-1.

Записав полученное соотношение для нормированного значения ξ/ξ₁ и подставив выражения (ξ₁ — ξ) из (3.65), получим

l_N(ξ) = (1 — ξ)/u_N u_N-2/u_N-1. (3.66)

Так как u_N-2/u_N-1 < 1, то из (3.66) следует справедливость неравенства (3.64). Случай 2. u_N-2/u_N < ξ/ξ₁ ≤ 1/2. Из соотношения (3.65) можем записать

ξ/ξ₁ = 1/(1 + (1 — ξ)/ξ u_N-2/u_N),

что должно быть меньше 1/2 или

(1 + (1 — ξ)/ξ u_N-2/u_N) > 2

Отсюда следует, что (1 — ξ)/u_N ≥ ξ/u_N-2. (3.67)

Точка минимума х* принадлежит интервалу [0, ξ₁], для которого после «проведения (N — 1)-го испытания согласно (3.60) получаем для нормированного значения ξ/ξ₁ выражение

l_N(ξ) = ξ₁l_N-1(ξ) = ξ/u_N-2

так как ξ < 1/2. Отсюда, с учетом (3.67), следует справедливость неравенства (3.64). Случай 3:

1/2 < ξ/ξ₁ ≤ u_N-1/u_N

По симметрии можем записать

l_N (ξ)= ξ₁(1 — ξ) = ξ₁l_N-1(1 — ξ).

Для нормированного значения ξ/ξ₁ после проведения (N — 1)-го испытания согласно (3.60) получаем

l_N(ξ) = (ξ₁ — ξ)/u_N-2

Подставляя сюда (ξ₁ — ξ) из выражения (3.65), можем записать

l_N(ξ) = (1 — ξ)/u_N.

Таким образом, неравенство (3.64) доказано для всех трех случаев, исчерпывающих возможные ситуации. Следовательно, неравенства (3.63) и (3.64) одновременно могут иметь место, если

l_N(ξ) = (1 — ξ)/u_N.

Аналогично доказывается выполнение соотношения (3.60) при
u_N-1/u_N+1 < ξ ≤ 1/2 для N испытаний при условии, что оно справедливо для (N - 1)-го испытания. Из (3.60) следует, что при ξ = 0 и ξ = 1 (в случае, когда дополнительная информация о значении функции Q (х) относится к одному из концов априорного интервала неопределенности) длина апостериорпого интервала неопределенности [а_N, b_N] совпадает с оценкой, гарантируемой методом Фибоначчи:

l_N (0) = l_N (1) = l_N (F²) = 1/u_N.

В общем случае дополнительная информация о значениях унимодальной функции Q (х) на обоих концах априорного интервала неопределенности Q (0) и Q (1) не позволяет получить оценку l_N (ξ) лучше, чем она гарантируется методом Фибоначчи, т. е. эта информация является избыточной.

Предположим от противного, что существует процедура сокращения интервала неопределенности F, использующая информацию о значениях Q (0) и Q (1) которая позволяет получить апостериорный интервал неопределенности, длина которого меньше оценки, гарантируемой методом Фибоначчи:

l_N(F) < l_N(F²). (3.68)

Построим для произвольной унимодальной функции Q (х) ее нижнюю оценку.

Q*(x) = Q(0) для x = 0;
Q*(x) = Q(x) — max(Q((0), Q(1)) для 0 < x <1 Q*(x) = Q(1) для x = 1;

Нетрудно видеть, что для построенной функции Q (х) справедливо неравенство (3.68), т. е. течка ее минимума x* может быть локализована с помощью метода F в апостериорном интервале неопределенности, длина которого не больше l_N(F²). С другой стороны, согласно построению функция Q (х) является унимодальной и ее минимум совпадает с точкой минимума функции Q (х), но для последней наилучшим является метод Фибоначчи F², который гарантирует выполнение условия:

l_N(F²) < l_N(F).

Полученное неравенство противоречит допущению (3.68), что позволяет сделать вывод о том, что длина апостериорного интервала неопределенности [a_N, b_N] для произвольной унимодальной функции Q (х) зависит от длины априорного интервала неопределенности [a, b] и числа проведенных испытаний N, но не зависит от информации о значениях функции Q (а) и Q(b), вычисленных на концах интервала неопределенности.

В некоторых случаях, кроме информации о значениях функции Q (х) в фиксированных точках, относительно свойств унимодальной функции могут быть априори получены дополнительные сведения. Например, введена опенка первых разностей-функции Q (х) в виде константы Липшица или известно, что минимизируемая функция является выпуклой и т. д.

Предположим, что рассматриваемый класс унимодальных функций включает только функции Q (х), которые удовлетворяют условию Липшица с известной константой L:

|Q(x₁ — Q(x₂)| ≤ L|x₁ — x₂| для x₁, x₂ ∈ [a, b]. (3 69)

Для непрерывных функций Q (х)∈С¹ константа Липшица равна максимальному значению первой производной от этой функции

L = max |∂Q/∂x|

а для выпуклых функций Q (х) она может быть определена из выражения:

L = max {|Q'(a+0)|, |Q'(b-0)|},

где

Q'(a+0) = [Q(a + Δ) — Q(a)]/Δ;
Q'(b-0) = [Q(b) — Q(b — Δ)]/Δ;

Рассмотрим алгоритм, относящийся к классу методов сокращения интервала неопределенности. Основная идея этого алгоритма заключается в том, что на k-м шаге поиска с помощью известной константы Липшица Щ строятся ломаные, позволяющие получить текущий интервал неопределенности [a_k‘, b_k‘] меньших размеров, чем при помощи метода Фибоначчи.

Геометрическая иллюстрация-процедуры сокращения длины текущего интервала неопределенности с помощью построения отрезков прямых в углом наклона, равным константе Липшица L, приведена на рис. 3.6.

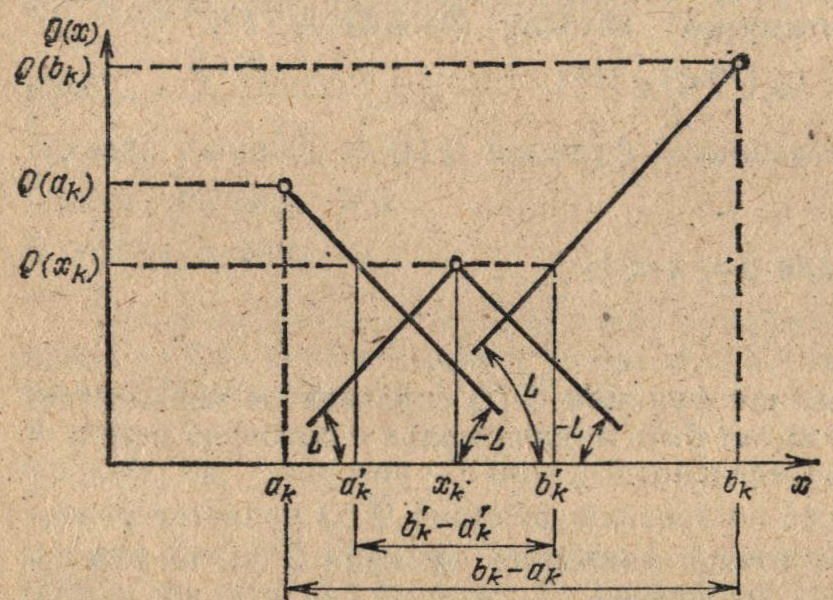
Рис. 3.6. Сокращение длины текущего интервала неопределенности с помощью построения отрезков прямых с углом наклона, равным константе Липшица L

Здесь показана ситуация, которая имеет место после проведения k испытаний:

Q(x_k) = min Q(x_i);
а_k < x_k < b_k; (3.70)
Q (a_k) > Q (x_k) < Q (b_k).

Из рис. 3.6 видно, что проведение через точки с координатами (a_k, Q (a_k)), (x_k, Q (x_k)) и (b_k, Q (b_k)), отрезков прямых с тангенсами углов наклона к оси х, равными L и (- L), позволяет выделить интервал неопределенности [a_k‘, b_k‘], который получается путем пересечения построенных ломаных с прямой Q (х) = Q (x_k) = const. (Для метода Фибоначчи в рассмотренной ситуации (3.70) интервал неопределенности равен отрезку [a_k, b_k]). Нетрудно видеть, что унимодальная функция Q (х), удовлетворяющая условию (3.69), обладает следующими свойствами:

график функции Q (х) на интервале [a_k, b_k] располагается не ниже построенных ломаных, так как для любых значений x_k из условия Липшица (3.69) следует неравенство

Q(x) ≥ (Q(_k) — L|x — x_k|);

точка минимума х* функции Q (х) принадлежит интервалу [a_k‘, b_k‘], что позволяет исключить из дальнейшего рассмотрения подынтервалы [а_k, а_k‘] и [b_k‘, b_k‘] длина текущего интервала неопределенности [a_k‘, b_k‘] зависит от константы Липшица L и убывает с уменьшением ее значения.

Таким образом, на каждом шаге поиска путем обработки результатов предыдущих испытаний с учетом константы Липшица осуществляется уменьшение текущего интервала неопределенности, содержащего точку минимума х*. При этом могут встретиться следующие ситуации.

I. Функция Q (х) не вычислена еще ни в одной точке. Интервал неопределенности [a_k‘, b_k‘] совпадает с исходным интервалом неопределенности [а, b].

II. Среди вычисленных значений Q (х) оказалось два одинаковых (рис. 3.7, а). Тогда концы интервала неопределенности [a_k‘, b_k‘] совпадают с точками, где получились эти значения.

III. Функция Q (х) вычислена лишь в одной точке x_k (рис. 3.7, б). Интервал неопределенности [a_k‘, b_k‘] совпадает с исходным интервалом [а_k, b_k].

IV. Среди k вычисленных значений Q (х) имеется минимальное Q (x_k), слева и справа от которого есть точки a_k, b_k, в которых значения функции Q (х) больше Q (x_k) (рис. 3.6). Этот общий случай приведен в стандартной форме на рис. 3.7, в. Интервал неопределенности [a_k‘, b_k‘] определяется из соотношений:

Q (a_k) — L (a_k‘ — a_k) = Q(x_k),
Q (b_k) — L(b_k — b_k‘) = Q(x_k).

V. Между точкой x_k и одним из концов исходного интервала [x_k, b] нет точек, где функция Q (х) вычислялась.

Если это подынтервал [x_k, b] (рис. 3.7, г), тогда конец интервала неопределенности b_k‘ совпадает с точкой b_k, а начало а_k‘ определяется из соотношения:

Q (a_k) — L (a_k‘ — a_k) = Q(x_k).

Если испытания не проводились в подынтервале [a, x_k] (рис. 3.7, д), то a_k‘ = a, a b_k‘ определяется из соотношения:

Q (b_k) — L(b_k— b_k‘) = Q(x_k).

На рис. 3.7 показаны рассмотренные типовые ситуации, причем справа приведены их стандартные формы, полученные при помощи замены переменных:

t = (х — а_k‘)/(b_k‘ — а_k‘),
z = 2 [Q (х) — Q (x_k)]/L,
ξ = (x_k — а_k‘)/(b_k‘ — a_k‘).

Эти преобразования позволяют свести интервал неопределенности [a_k‘, b_k‘] к интервалу единичной длины [0, 1], а испытание в точке (x_k, Q (x_k)) преобразовать в точку о координатами (ξ, 0). Теперь для каждой из пяти ситуаций (рис. 3.7) и любого целого числа m оставшихся вычислений функции Q(x) необходимо указать процедуру определения точки х_m (ξ) ∈ [0, 1], в которой требуется провести очередное испытание.

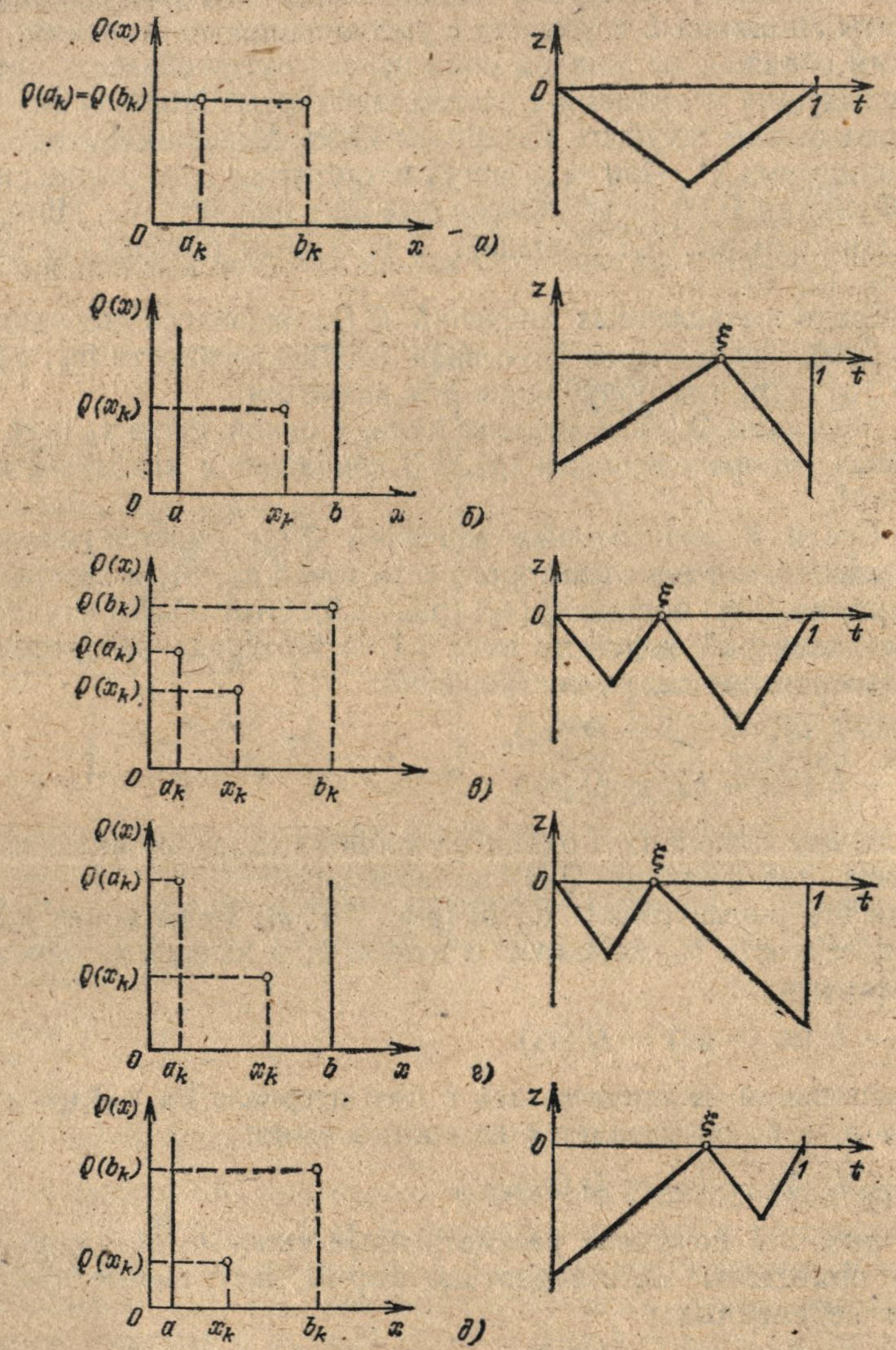
Рис. 3.7. Типовые ситуации и их стандартные формы определения интервала неопределенности [a_k‘, b_k‘] в алгоритме F⁴

Для ситуаций I и II потребуем, чтобы рассматриваемый метод F* совпадал с методом Фибоначчи. Тогда, приняв ξ = 0 или ξ = 1, точку очередного испытания х_m(ξ) будем выбирать по одной из формул алгоритма F²:

х_m(0) = u_m-1/u_m+1 или х_m(1) = u_m/u_m+1.

В остальных трех ситуациях (III—V) для интервала неопределенности [0, 1] имеется дополнительная информация о значении функции Q (х) во внутренней точке ξ. В этом случае для получения наименьшего значения апостериорного интервала неопределенности l_m (ξ) точка очередного испытания х_m(ξ) должна определяться из выражения (3.65):

x_m(ξ) = ξ + (1 — ξ)u_m-2/u_m при 0 < ξ < 1/2; x_m(ξ) = ξu_m-1/u_m при 1/2 < ξ < 1; где m = N-1, N - 2, ..., 1.

Окончательно стратегия поиска минимума унимодальной функции Q (х), определенной на интервале [а, b], по алгоритму F⁴ сводится к следующей последовательности действий.

1. На первом шаге поиска (k = 1) принимается m = N; а_k = а; b_k = b и ξ = 0.
2. Для ситуации 1 определяется точка очередного испытания х_m(ξ) = u_m-1/u_m+1.
3. Вычисляется значение функции Q (х) в точке

x_i = a_k + (b_k — a_k)x_m (ξ);

4. Обрабатываются результаты проведенных k испытаний:

Q (x_k) = min Q(x_j);

5. Определяется одна из четырех типовых ситуаций II—V; с помощью константы Липшица L строятся ломаные, проходящие через точки (a_k, Q (a_k)), (x_k, Q (x_k)) и (b_k, Q(b_k)), и находится текущий интервал неопределенности [a_k‘, b_k‘], содержащий точку минимума х*.

6. Определяются параметр ξ = (x_k — a_k‘)/(b_k — a_k‘) и число оставшихся испытаний m = m — 1. Если m = 1, то переходят к п. 8. В противном случае выполняется п. 7.

7. Вычисляется точка очередного испытания

х_m(ξ) = ξ + (1 — ξ)u_m-2/u_m, если 0 ≤ ξ ≤ 1/2;
х_m(ξ) = ξu_m-1/u_m — в противном случае

и вся процедура повторяется с п. 3.
8. Находится апостериорный интервал неопределенности [а_N, b_N].

Для этого последнее N-е испытание проводится в точке

x_i = a_k‘ + (b_k‘ — а_k‘)ξ₁,

Рассмотренный алгоритм F⁴ является обобщением метода Фибоначчи на класс унимодальных функций с известной константой Липшица L. Поэтому при L → ∞ он просто совпадает с алгоритмом. Однако для любой промежуточной ситуации учет конечного значения L уменьшает текущий интервал неопределенности [_k, b_k] да значения [а_k‘, b_k‘], что позволяет получить при одном и том же числе испытаний N более точную оценку апостериорного интервала неопределенности [a_N, b_N] содержащего точку минимума х*. Алгоритм F⁴ отличается от алгоритма F² тем, что на каждом шаге решение о том, какой подынтервал исключить из дальнейшего рассмотрения делается по информации не только о значении числа оставшихся испытаний т, но и по информации о значении параметра ξ. Этот параметр позволяет адаптировать алгоритм поиска к особенностям минимизируемой функции Q (х).

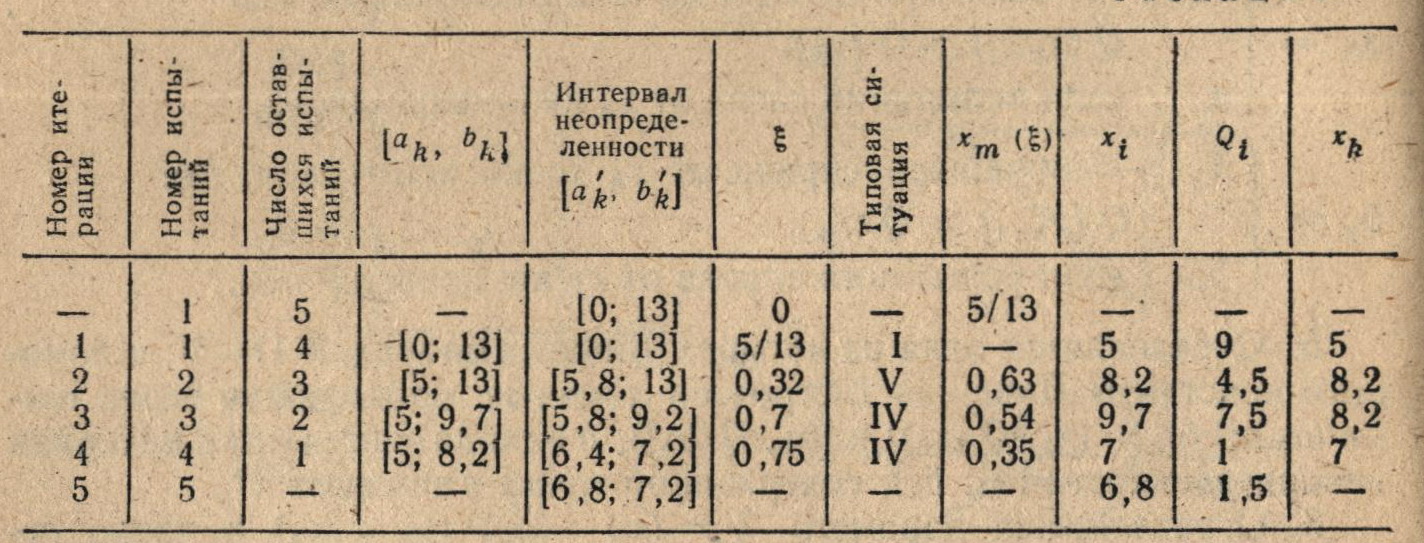
Для примера, приведенного на рис. 3.2, стратегия выбора точек испытаний по алгоритму F⁴ приведена в табл. 3.2. Из таблицы видно, что учет константы Липшица (здесь L = 6) позволяет уменьшить апостериорный интервал неопределенности по сравнению с методом Фибоначчи при одном и том же числе допустимых испытаний (N = 5) больше чем в два раза.

Таблица 3.2

Комментарии запрещены.