Образовательный блог — всё для учебы

Другой подход к решению задачи локализации точки глобального минимума X* многопараметрической функции Q (x₁, x₂, …, x_n) связан с использованием коллектива независимых стохастических автоматов как некоторой системы поисковой оптимизации.
Прочитать остальную часть записи »

Материал данного поста является вспомогательным, хотя и весьма важным. Поэтому здесь приводятся доказательства не всех формулируемых утверждений. Кроме того, здесь не будут приводиться обобщения (иногда достаточно содержательные) этих утверждений.

Повсюду в этом посте будем предполагать, что все рассматриваемые случайные величины принимают значения в метрическом пространстве Ψ, наделенном метрикой ρ. В дальнейшем в качестве таких случайных величин будут рассматриваться состояния процесса z_t, для которого соответствующие метрики введены в марковских процессах с дискретным временем.
Прочитать остальную часть записи »

Рассмотрим обобщение метода F²¹ поиска точки глобального минимума произвольной кривой с помощью стохастического автомата на случай многопараметрических положительных функций Q (х).

Каждый интервал [0, c_i] изменения i-й переменной разделим на K_i отрезков равной длины

ω_i = c_i/K_i, i =1, 2, …, n. (6.35)

Прочитать остальную часть записи »

Теорема 1. Если распределение {a(t)}, t ≥ 1, арифметическое с шагом 1, {a(t)}∈NP(N, а), и μ = ∑ta(t) < ∞,то справедлива оценка Прочитать остальную часть записи »

В таких СУБД (т.е. в SQL Server) часть функций по управлению базой данных оформляется в виде объектов, хранящихся в самой базе данных, а сервер реализует эти вот возможности в процессе работы.

• Во-первых, для этих целей используются процедуры базы данных, к которым возможно указать права доступа и использования.
Прочитать остальную часть записи »

Будем предполагать, что минимизируемая функция Q(x) в задаче принадлежит классу K_L функций, удовлетворяющих условию типа условия Липшица с известной константой L:

|Q(x¹) — Q(x²)| ≤ Lρ(x¹, x²), x¹, x²∈D_x, (6.10)

Прочитать остальную часть записи »

От работы топки во многом зависит экономичная и надежная работа котла в целом. Поэтому независимо от классификационной принадлежности она должна удовлетворять требованиям:

• Быть технологичной в изготовлении
• Быть монтажепригодной (удобство монтажа)
• Обеспечивать удобство эксплуатации и ремонта
• Обеспечивать экономичное сжигание расчетных видов топлив (в заданном диапазоне нагрузок котла)
    • Газ, мазут — 30…100%D_ном
    • Твердое топливо + ТШУ — 50…100%D_ном
    • Твердое топливо + ЖШУ — 70…100%D_ном
Прочитать остальную часть записи »

Цель настоящего примера — показать, как свойство достижимости может быть использовано в несколько необычной ситуации— для оценки скорости сходимости. Пусть {ξ_i} — последовательность независимых одинаково распределенных случайных величин, принимающих следующие значения:
S_n = ∑ξ_i, n ≥ 1; a(t) = P {ξ_i=t}, H(t) = P {ξ_i≥t}; h(t) = P{∪(S_i = t)}, t = 1,2 ..
Прочитать остальную часть записи »

Определение: Функция, совпадающая со своей двойственной функцией, называется самодвойственной.

Замечание: Если функция f(x₁, x₂,…,x_n) самодвойственна, то функция ¬f также самодвойственна, то есть
(⌈f(x₁, x₂,…,x_n))*=⌈(⌈f(⌈x₁,…, ⌈x_n))= [функция самодвойственна f=f*] = ⌈f(x₁, …, x_n).
Прочитать остальную часть записи »

Поскольку результаты данного поста использоваться далее не будут, мы их приведем без доказательства. Будет рассмотрен лишь случай непрерывного времени. Распространение на дискретное время очевидно.

Пусть μ и μ* — стационарные распределения, рассмотренные в теореме 5.4. Пусть f(z) —некоторая функция, интегрируемая по распределению μ. Рассмотрим последовательность случайных величин (ξ_n}, где

ξ_n = ∫f(z_t)dt, n ≥ 1, τ₀⁽¹⁾ = 0, (1)

Прочитать остальную часть записи »

Пусть минимизируемая функция Q (х) зависит от небольшого числа переменных (n ≤ 3). В этом случае для решения задачи поиска глобального минимума x* непрерывной функции Q (х), определенной в n-мерном гиперпараллелепипеде D_x = {x|a_i ≤ x_i ≤ b_i , i = 1, 2,…, n}

min Q(x₁, x₂, …, x_n), (6.1)

Прочитать остальную часть записи »

Приведем сначала вариант теоремы 3.1 для процессов с непрерывным временем. Здесь, как и раньше, через η^Q обозначим момент первого достижения множества Q⊂Z, а через θ^R — момент первого выхода из множества {||z|| < R}. Прочитать остальную часть записи »

При решении задачи оптимального проектирования часто приходится иметь дело с математическими моделями, в которых не имеется аналитических выражений для первых производных минимизируемой функции Q(х). В связи с чем поиск оптимального решения х* приходится вести по результатам вычислений функции Q (х). Методы, которые используют для выбора точки очередного испытания х^r информацию только о значениях функции Q (х), называются методами прямого поиска (методами нулевого порядка, методами минимизации без вычисления производных).
Прочитать остальную часть записи »

Мы сохраним в этом посте основные обозначения принятые ранее. Именно, будет рассматриваться случайный момент времени η_Q* первого достижения множества Q, определяемый формулой

η_Q = inf {t:z_t∈Q, t>0}.

Прочитать остальную часть записи »

Рассмотрим класс алгоритмов, которые основаны на квадратичной аппроксимации минимизируемой функции Q (х) в Δ-окрестности каждого приближения x^r разложением в ряд Тейлора. В связи с тем, что для определения очередного приращения Δ^r эти алгоритмы требуют вычисления первых и вторых производных функций Q (х), они получили название методов второго порядка.
Прочитать остальную часть записи »

Если в предыдущем посте изучались некоторые свойства времени первого возвращения траекторий z_t, то здесь будут анализироваться свойства, связанные со значениями, принимаемыми процессом z_t, хотя эти свойства и тесно связаны между собой.
Прочитать остальную часть записи »

Определение минимального значения многопараметрической функции Q (х), заданной в n-мерном евклидовом пространстве связано с решением задачи безусловной оптимизации:

min Q(x₁, х₂,…, x_n). (5.1)

Здесь каждая переменная x_i, i= 1, 2, …, n, может принимать значения от -∞ до +∞. Предположим, что функция Q (х) является унимодальной функцией, для которой в каждой точке х может быть получено с помощью градиента ∇Q(х)= {∂Q/∂x₁, …, ∂Q/∂x_n), а при необходимости и гессиана (матрицы вторых производных)
Прочитать остальную часть записи »

Пусть Q — некоторое подмножество Z. Обозначим через η^Q момент первого достижения множества Q траекторий рассматриваемого процесса z_t, т. е.

η^Q = min{t: z_t∈Q, t>0}; (1)

Отметим, что с формальной точки зрения вместо момента первого достижения можно было бы рассматривать момент первого выхода, поскольку η^Q = θ^Z\Q. Однако, как было сказано во введении, изучение указанных случайных величин приводит к различным прикладным задачам.
Прочитать остальную часть записи »

Стратегия поиска точки глобального минимума х* по алгоритму F²⁰*с помощью автомата Буша—Мостеллера сводится к следующей последовательности действий.

1. Задаются одинаковые значения вероятностей выбора состояний автомата p_j(r) = 1/М, j = 1,2, …, М, и принимается Q_j* = A_∞ для всех j = 1, 2, …, М, где A_∞ — положительное большое число.
Прочитать остальную часть записи »

Рассмотрим некоторое множество Ψ действительных случайных величин. Общий элемент этого множества обозначим ξ. Поскольку нас будут интересовать лишь маргинальные (частные) распределения случайных величин ξ∈Ψ, то безразлично, заданы эти величины на одном вероятностном пространстве или нет. Предположим, что у всех ξ∈Ψ существуют конечные средние Мξ.
Прочитать остальную часть записи »

Рассмотрим класс алгоритмов, поиск точки глобального минимума X* в которых основан на теории автоматов.

Под автоматом будем понимать динамическую систему, которая в дискретные моменты времени r = 1, 2 ,3, …, воспринимая на входе сигнал у(r), изменяет свое внутреннее состояние S (r) согласно уравнению:

S(r) = φ₁[у(r), S (r — 1)] S(0) = S₀. (4.75)

Прочитать остальную часть записи »

Пример схемы резервирования с конечным временем переключения элементов.

Рассмотрим следующую систему (рис. 5), состоящую из n идентичных элементов.

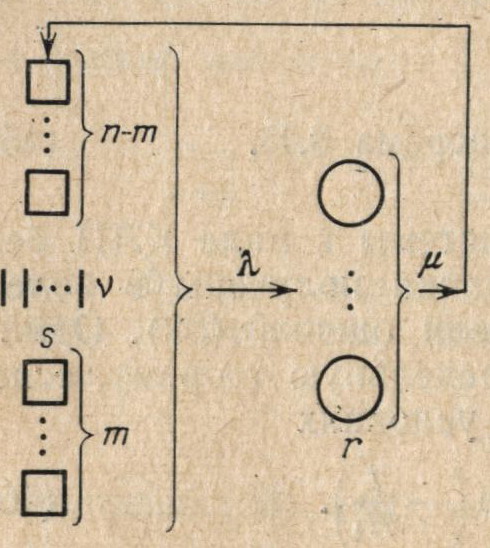
В полностью исправном состоянии в системе имеются m элементов, находящихся на рабочих местах («рабочих» элементов), n—m элементов, находящихся в нагруженном (горячем) резерве («резервных» элементов). При выходе какого-либо рабочего элемента из строя он мгновенно поступает на одно из r ремонтных мест, r ≤ n, если имеется свободное, либо становится в очередь на ремонт. Замена отказавших элементов происходит следующим образом. Если в наличии есть хотя бы один резервный элемент, а общее количество работающих и подключаемых элементов меньше m, то этот резервный элемент немедленно начинает переключаться с резервного места на рабочее. Время переключения каждого отдельного элемента — случайная величина с функцией распределения 1—е^-vx. Дополнительно предположим, что число одновременно переключаемых элементов не может превышать некоторого числа s. Элементы системы являются ненадежными и могут отказывать как на рабочих местах, так и в резерве и в состоянии переключения. Будем называть элемент исправным, если он находится в одном из этих трех состояний: рабочем, резервном и переключения. Время пребывания элемента в исправном состоянии является, по предположению, случайной величиной с функцией распределения 1-е^-λx. Время ремонта отдельного элемента также случайно и имеет функцию распределения 1-е^-μx. Все перечисленные случайные величины независимы в совокупности.
Прочитать остальную часть записи »

Процедура поиска точки глобального минимума х* аппроксимирующей модели может быть упрощена, если в качестве математической модели использовать кусочно-кубическую кривую S_N(х), проходящую через точки испытаний (x_i, Q(x_i)), i = 1, 2, …, N, и моделирующую поведение функции Q (х) на отдельных отрезках интервала |a, b| полиномами третьей степени Р₃(х) = ∑α_kⁱx^k. В этом случае поиск точки глобального минимума х* произвольной кривой Q (х) может быть осуществлен с помощью метода кусочно-кубической аппроксимации F¹⁵, в котором точки испытаний на каждом k-м шаге выбираются независимо от информации о поведении функции Q(x) и равномерно располагаются на интервале [a, b]:

x_i^(k) = a + i(b-a)/(N_k-1), i = 0, 1, …, N_k — 1.

Прочитать остальную часть записи »

Ненагруженное дублирование с восстановлением.

Данный пример можно рассматривать как развитие предыдущего примера в силу сделанного в конце его замечания.

Итак, рассмотрим дублированную систему, описанную в конце предыдущего примера. Опишем сначала работу такой системы в виде КЛП без непрерывного вмешательства случая. Поскольку функционирование системы рассматривается лишь до момента первого отказа, то будем для простоты считать «отказовые» состояния поглощающими. Но, очевидно, до момента первого отказа работа рассматриваемой системы эквивалентна работе однолинейной системы обслуживания с ожиданием, если отождествить попарно следующие понятия: отказ работающего элемента и поступление в систему очередного требования, длительность ремонта и длительность обслуживания, отказ системы и наличие в системе обслуживания более одного требования. Поэтому в качестве КЛП, описывающего изучаемую дублированную систему, можно взять КЛП примера 1.4.4, положив в нем N = 1, В = G и, считая состояния v > 1 поглощающими, объединить их в одно поглощающее состояние v = 2, |2| = 0. Тогда дополнительные координаты имеют следующий смысл:
Прочитать остальную часть записи »

Рассмотрим класс алгоритмов, поиск глобального минимума по которым сводится к следующей последовательности действий:

1) проводятся испытания в точках x_i, i = 1, 2,…, N, расположенных определенным образом на интервале [a, b];

2) по полученным значениям (x_i, Q (x_i)), i = 1,2,…, N, строится математическая модель, аппроксимирующая функцию Q (х) на интервале [a, b];
Прочитать остальную часть записи »

Система имитационного моделирования может рассматриваться как машинный аналог сложного реального процесса.

На рис. 2.1 представлена укрупненная архитектура имитационной системы. Имитационная система должна иметь интеллектуальный интерфейс, т.е. обеспечивать удобное и эффективное взаимодействие широкого пользователя с ЭВМ.
Такой интеллектуальный интерфейс должен содержать средства дающие возможность:
Прочитать остальную часть записи »

В этом посте мы обобщим результаты, полученные ранее, на случай кусочно-линейных процессов. Вновь Q будет обозначать открытое множество в пространстве состояний Z, а θ^Q — момент первого выхода из указанного множества. Как было доказано ранее (это доказательство без изменений переносится и на непрерывное время), при τ = θ^Q∧u имеет место равенство

M_z[1 — χ_Q(z_τ)] = P_z{θ^Q≤u}.

Прочитать остальную часть записи »

Многопроцессорные ЭВМ открывают возможность одновременной оценки нескольких независимых значений функции Q (х) путем распараллеливания вычислений. В связи с чем для минимизации унимодальных функций могут быть построены параллельные алгоритмы поиска, в которых на каждом i-м шаге часть испытаний n_i ≤ N проводится одновременно в заданной совокупности точек х₁, х₂, …, х_n.
Прочитать остальную часть записи »

Пусть Т= {0, 1, 2, …}, z_t — однородный марковский процесс с пространством состояний Z. Обозначим через θ_Q(z) индикатор множества Q:

θ_Q(z) = 0, если z не принадлежит Q;
θ_Q(z) = 1, если z∈Q; (1)
Прочитать остальную часть записи »

Пусть после проведения k испытаний имеет место ситуация III (рис. 3.7, в, см. предыдущий пост): Прочитать остальную часть записи »