Архив рубрики «Анализ сложных систем»
Устойчивость регенерирующих процессов
В этом посте будет изучаться устойчивость, сформулированная в терминах маргинальных распределений, характеризующих регенерирующие процессы. За определение устойчивости можно взять определение 1.1, если в качестве h(zt, zt*) выбрать какое-либо расстояние, зависящее лишь от маргинальных распределений величин zt и zt* (ниже для определенности будет рассматриваться только расстояние Дадли d, «порождающее» слабую сходимость), а под μ(α, α*) понимать соответствующим образом введенную меру отклонения возмущенных параметров от невозмущенных, также определяемую маргинальными характеристиками процессов zt и zt*. Более подробная «расшифровка» μ(α, α*) будет дана ниже.
Прочитать остальную часть записи »
Устойчивость на всей оси времени
Ранее рассматривалась задача анализа устойчивости предельных режимов у изучаемых процессов. В соответствии с этим в расчет принимались либо меры отклонения финальных распределений (слабая устойчивость в пределе), либо меры отклонения, усредненные по времени (устойчивость в среднем по времени). Если априори известно, что рассматриваемая система функционирует «достаточно долго», то анализ устойчивости в смысле приведенных определений оправдан, практически важен и может дать существенную информацию относительно ее поведения. Однако такая ситуация встречается далеко не всегда. Часто длина отрезка функционирования заранее не определяется и неизвестна. Поэтому (и наряду с этим) неизвестно также «время вхождения» системы в установившийся режим. Не исключены и случаи отсутствия «установившегося режима». Эти обстоятельства ведут к необходимости изучения устойчивости, которая является равномерной относительно времени, а также скорости сходимости к финальным распределениям.
Прочитать остальную часть записи »
Примеры устойчивости предельных режимов
Во всех приводимых ниже примерах равномерная независимость процесса от начального состояния проверяется путем не слишком сложного построения конкретных множеств ВN для которых выполнены свойства (2.24) и (2.25).
Пример 1. Многолинейная система обслуживания с ожиданием. Рассмотрим процесс zt введенный в примере 1.2.3:
zt+1 = R(zt + ηte — θtI)+. (1)
Постановка задачи устойчивости предельных режимов
Рассмотрим однородный марковский процесс zt, задаваемый рекуррентным соотношением вида (1.1.5), т. е.
zt+1 = F(zt, ξt), t≥0. (1)
Хотя результаты, приводимые в этой и следующей главах, имеют более общий характер, все же всюду будет считаться, что zt задается именно соотношением вида (1). Будем смотреть на это соотношение как на преобразование «управляющей» последовательности {ξt} и начального состояния z0 в последовательность {zt} (удобно начальное состояние z0 считать, с одной стороны, управляющим параметром, а с другой — управляемым).
Прочитать остальную часть записи »
Сходимость и метрики
Материал данного поста является вспомогательным, хотя и весьма важным. Поэтому здесь приводятся доказательства не всех формулируемых утверждений. Кроме того, здесь не будут приводиться обобщения (иногда достаточно содержательные) этих утверждений.
Повсюду в этом посте будем предполагать, что все рассматриваемые случайные величины принимают значения в метрическом пространстве Ψ, наделенном метрикой ρ. В дальнейшем в качестве таких случайных величин будут рассматриваться состояния процесса zt, для которого соответствующие метрики введены в марковских процессах с дискретным временем.
Прочитать остальную часть записи »
Теоремы достижимости и ограниченности
Теорема 1. Если распределение {a(t)}, t ≥ 1, арифметическое с шагом 1, {a(t)}∈NP(N, а), и μ = ∑ta(t) < ∞,то справедлива оценка Прочитать остальную часть записи »
Оценка скорости сходимости в теореме восстановления
Цель настоящего примера — показать, как свойство достижимости может быть использовано в несколько необычной ситуации— для оценки скорости сходимости. Пусть {ξi} — последовательность независимых одинаково распределенных случайных величин, принимающих следующие значения:
Sn = ∑ξi, n ≥ 1; a(t) = P {ξi=t}, H(t) = P {ξi≥t}; h(t) = P{∪(Si = t)}, t = 1,2 ..
Прочитать остальную часть записи »
Усиленный закон больших чисел
Поскольку результаты данного поста использоваться далее не будут, мы их приведем без доказательства. Будет рассмотрен лишь случай непрерывного времени. Распространение на дискретное время очевидно.
Пусть μ и μ* — стационарные распределения, рассмотренные в теореме 5.4. Пусть f(z) —некоторая функция, интегрируемая по распределению μ. Рассмотрим последовательность случайных величин (ξn}, где
ξn = ∫f(zt)dt, n ≥ 1, τ0(1) = 0, (1)
Ограниченность для КЛП
Приведем сначала вариант теоремы 3.1 для процессов с непрерывным временем. Здесь, как и раньше, через ηQ обозначим момент первого достижения множества Q⊂Z, а через θR — момент первого выхода из множества {||z|| < R}. Прочитать остальную часть записи »
Достижимость для КЛП
Мы сохраним в этом посте основные обозначения принятые ранее. Именно, будет рассматриваться случайный момент времени ηQ* первого достижения множества Q, определяемый формулой
ηQ = inf {t:zt∈Q, t>0}.
Ограниченность для процессов с дискретным временем
Если в предыдущем посте изучались некоторые свойства времени первого возвращения траекторий zt, то здесь будут анализироваться свойства, связанные со значениями, принимаемыми процессом zt, хотя эти свойства и тесно связаны между собой.
Прочитать остальную часть записи »
Достижимость для процессов с дискретным временем
Пусть Q — некоторое подмножество Z. Обозначим через ηQ момент первого достижения множества Q траекторий рассматриваемого процесса zt, т. е.
ηQ = min{t: zt∈Q, t>0}; (1)
Отметим, что с формальной точки зрения вместо момента первого достижения можно было бы рассматривать момент первого выхода, поскольку ηQ = θZ\Q. Однако, как было сказано во введении, изучение указанных случайных величин приводит к различным прикладным задачам.
Прочитать остальную часть записи »
Равномерно интегрируемые случайные величины
Рассмотрим некоторое множество Ψ действительных случайных величин. Общий элемент этого множества обозначим ξ. Поскольку нас будут интересовать лишь маргинальные (частные) распределения случайных величин ξ∈Ψ, то безразлично, заданы эти величины на одном вероятностном пространстве или нет. Предположим, что у всех ξ∈Ψ существуют конечные средние Мξ.
Прочитать остальную часть записи »
Схема резервирования с конечным временем переключения элементов
Пример схемы резервирования с конечным временем переключения элементов.
Рассмотрим следующую систему (рис. 5), состоящую из n идентичных элементов.
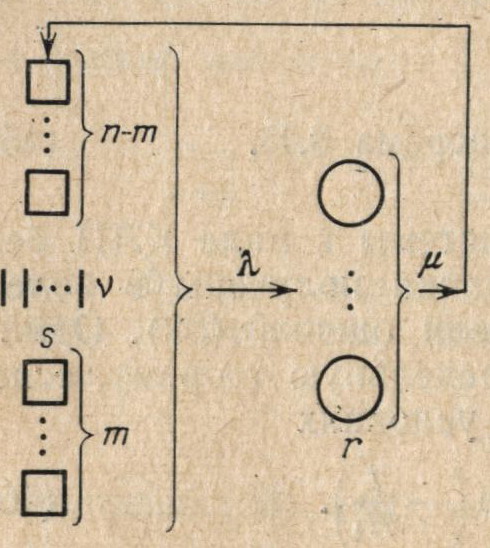
В полностью исправном состоянии в системе имеются m элементов, находящихся на рабочих местах («рабочих» элементов), n—m элементов, находящихся в нагруженном (горячем) резерве («резервных» элементов). При выходе какого-либо рабочего элемента из строя он мгновенно поступает на одно из r ремонтных мест, r ≤ n, если имеется свободное, либо становится в очередь на ремонт. Замена отказавших элементов происходит следующим образом. Если в наличии есть хотя бы один резервный элемент, а общее количество работающих и подключаемых элементов меньше m, то этот резервный элемент немедленно начинает переключаться с резервного места на рабочее. Время переключения каждого отдельного элемента — случайная величина с функцией распределения 1—е-vx. Дополнительно предположим, что число одновременно переключаемых элементов не может превышать некоторого числа s. Элементы системы являются ненадежными и могут отказывать как на рабочих местах, так и в резерве и в состоянии переключения. Будем называть элемент исправным, если он находится в одном из этих трех состояний: рабочем, резервном и переключения. Время пребывания элемента в исправном состоянии является, по предположению, случайной величиной с функцией распределения 1-е-λx. Время ремонта отдельного элемента также случайно и имеет функцию распределения 1-е-μx. Все перечисленные случайные величины независимы в совокупности.
Прочитать остальную часть записи »
Пример — ненагруженное дублирование с восстановлением
Ненагруженное дублирование с восстановлением.
Данный пример можно рассматривать как развитие предыдущего примера в силу сделанного в конце его замечания.
Итак, рассмотрим дублированную систему, описанную в конце предыдущего примера. Опишем сначала работу такой системы в виде КЛП без непрерывного вмешательства случая. Поскольку функционирование системы рассматривается лишь до момента первого отказа, то будем для простоты считать «отказовые» состояния поглощающими. Но, очевидно, до момента первого отказа работа рассматриваемой системы эквивалентна работе однолинейной системы обслуживания с ожиданием, если отождествить попарно следующие понятия: отказ работающего элемента и поступление в систему очередного требования, длительность ремонта и длительность обслуживания, отказ системы и наличие в системе обслуживания более одного требования. Поэтому в качестве КЛП, описывающего изучаемую дублированную систему, можно взять КЛП примера 1.4.4, положив в нем N = 1, В = G и, считая состояния v > 1 поглощающими, объединить их в одно поглощающее состояние v = 2, |2| = 0. Тогда дополнительные координаты имеют следующий смысл:
Прочитать остальную часть записи »
Оценки в случае непрерывного времени
В этом посте мы обобщим результаты, полученные ранее, на случай кусочно-линейных процессов. Вновь Q будет обозначать открытое множество в пространстве состояний Z, а θQ — момент первого выхода из указанного множества. Как было доказано ранее (это доказательство без изменений переносится и на непрерывное время), при τ = θQ∧u имеет место равенство
Mz[1 — χQ(zτ)] = Pz{θQ≤u}.
Оценки в случае дискретного времени
Пусть Т= {0, 1, 2, …}, zt — однородный марковский процесс с пространством состояний Z. Обозначим через θQ(z) индикатор множества Q:
θQ(z) = 0, если z не принадлежит Q;
θQ(z) = 1, если z∈Q; (1)
Прочитать остальную часть записи »
Постановка задачи оценки распределения момента первого достижения
Многие важные задачи анализа систем могут быть сформулированы в терминах момента первого достижения. Поэтому различные оценки распределения этого момента важны в первую очередь с практической точки зрения.
Сформулируем задачу, которая будет решаться в данной главе.
Прочитать остальную часть записи »
Пример процесс рождения и гибели. Многолинейная система массового обслуживания с относительным приоритетом
Пример 1. Процесс рождения и гибели. Рассмотрим вероятностный процесс, широко применяемый в различных прикладных областях. Это процесс со счетным числом состояний N = {0, 1, 2, …}. В каждом состоянии v∈N процесс проводит случайное время, которое распределено экспоненциально с параметром λ(v), после чего переходит либо в состояние v + 1 (с вероятностью pv), либо в состояние v—1 (с вероятностью qv), q0 = 0, pv + qv = 1. Будем считать, что λ(v) > 0, v ≥ 0, pv > 0, v ≥ 0 и qv > 0, v ≥ 1. Из этих условий следует, что p0 = 1. Величина λ(v)pv трактуется как интенсивность рождения в состоянии v, а λ(v)qv — интенсивность гибели в этом же состоянии. Очевидно, что любая функция V(v), не принимающая бесконечных значений, принадлежит множеству DА. При этом вид оператора А (см. формулу (3.4), где нужно положить vv = 0) следующий:
AV(v) = λ(v) [pvV(v + 1) + qvV(v- 1) — V(v)]. (1)
Достаточные условия регулярности
Объектом изучения в данном посте и далее, если не оговорено противное, является процесс zt, построенный на последовательности необрывающихся процессов zt, n. Напомним, что одним из условий проведенных построений является необрываемость подпроцессов zt, n. В свою очередь достаточным условием для этого является выполнение леммы 2 с заменой Тδ на Tδ, n. Ниже без дополнительных оговорок будет считаться, что все подпроцессы zt, n необрывающиеся. Во всех примерах данной и последующих постов условия леммы 2 выполнены. Это обстоятельство также не будет всякий раз оговариваться.
Прочитать остальную часть записи »
Процесс, построенный на последовательности необрывающихся процессов
Условия леммы 1 достаточны для того, чтобы рассматриваемые процессы были необрывающимися. Однако существуют практически интересные задачи, требующие изучения процессов, у которых функции λ(z) и vv неограничены. Поэтому принципильно важно получить более широкие условия регулярности рассматриваемых процессов. Вместе с тем необходимо напомнить, что построения были проведены в предположении равномерной ограниченности λ(z) и vv (условие (1.3.2)). Поэтому, прежде чем переходить к получению соответствующих результатов, необходимо расширить класс изучаемых процессов.
Прочитать остальную часть записи »
Свойство регулярности. Необрывающиеся процессы
Вводные замечания
Необходимость изучения свойства регулярности возникает естественным образом при рассмотрении возможных типов поведения динамических (в широком смысле) систем. Оказывается, что при определенных условиях траектории могут за конечное время «уйти в бесконечность» или иметь бесконечное число скачков. Такое поведение обычно рассматривается как нежелательное или невозможное, поскольку в реальных системах уход координат в бесконечность за конечное время требует либо бесконечной мощности, либо бесконечной интенсивности расхода других ресурсов. Кроме того, со свойством регулярности тесно связаны и другие качественные свойства — ограниченность, устойчивость и свойства, определяемые моментами первого достижения и возвращения.
Прочитать остальную часть записи »
Пример многолинейной системы обслуживания с ожиданием
Многолинейная система обслуживания с ожиданием. Дадим теперь пример системы, по конструкции более простой, чем КЛП Гнеденко — Коваленко, но не укладывающейся в эту схему.
Рассмотрим систему массового обслуживания (в другом представлении она была рассмотрена в примере 3), состоящую из N приборов, на которую через независимые одинаково распределенные случайные промежутки времени поступают требования. Обозначим Н(х) функцию распределения этих промежутков. Длительности обслуживания отдельных требований на приборах не зависят от остальных случайных величин, «управляющих» системой, и имеют одну и ту же (для всех приборов и требований) функцию распределения В(х). Будем характеризовать состояние системы вектором z = (v, zv), v = 0, 1, …, где компоненты вектора z имеют следующий смысл: v — число требований, находящихся в системе, zv(1)—время, оставшееся до поступления очередного требования,
zv(j), 1 < j ≤ N ∧ v + 1 — времена, оставшиеся до окончания обслуживании требований, находящихся на приборах.
Прочитать остальную часть записи »
Модель узла связи как КЛП Гнеденко — Коваленко
Модель узла связи как КЛП Гнеденко — Коваленко. Предварим разбор примера кратким описанием системы. Рассмотрим сеть связи, задаваемую некоторым графом (рис. 2).
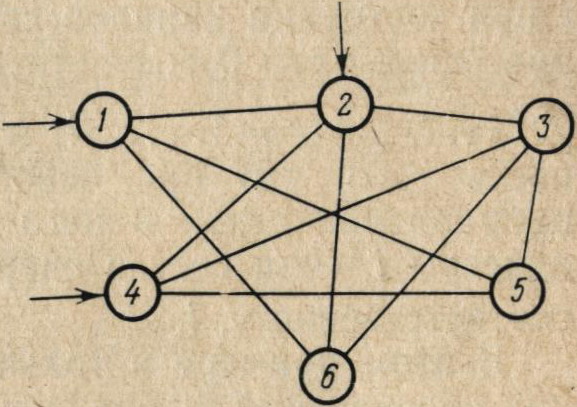
Рис. 2
Узлы графа соответствуют узлам связи, а дуги — направлениям связи. Система работает следующим образом. В не-которые моменты времени на отдельные узлы связи (на рис. 2 они отмечены номерами 1, 2, 4) извне поступают сообщения, подлежащие передаче по сети. Сообщения характеризуются, вообще говоря, рядом признаков: адресом, приоритетом, предельным сроком нахождения в сети и т. д. Узел связи в соответствии с алгоритмом своей работы либо посылает это сообщение в одно из примыкающих к нему направлений связи, либо запоминает его и хранит до ближайшего момента времени, когда появится возможность послать его в сеть. Указанные альтернативы определяются загрузкой сети, наличием свободных каналов связи и пр. Таким образом, в узле связи могут образовываться очереди из сообщений, ждущих своей отправки.
Рассмотрим узел связи вместе с выходящими из него направлениями связи. Пусть работа узла определяется алгоритмом A. Величины, которые характеризуют этот алгоритм, будем отмечать буквой A. Предположим, что рассматриваемый узел связи может посылать сообщения в R направлений связи, R ≥ 1, причем r-е направление (1 ≤ r ≤ R) состоит из mr каналов связи. По каждому из каналов связи одновременно может передаваться не более одного сообщения.
Прочитать остальную часть записи »
Пример многолинейной системы массового обслуживания с относительным приоритетом
Многолинейная система массового обслуживания с относительным приоритетом. Дадим пример описания конкретной системы обслуживания в виде КЛП Гнеденко—Коваленко.
Пусть в систему, состоящую из N обслуживающих приборов, поступают требования двух типов. Требования первого типа назовем приоритетными, а второго — обычными. Обслуживание однотипных требований происходит в порядке их поступления, и процесс обслуживания каждого требования идет без прерывания. В случае, если в момент поступления какого-либо требования имеется хотя бы один свободный прибор, оно немедленно начинает обслуживаться. В противном случае требование ожидает начала обслуживания. Если в момент освобождения прибора в системе находится хотя бы одно требование, то на обслуживание поступает требование наивысшего приоритета из имеющихся в системе. Если в некоторый момент в системе находятся v1 приоритетных и v2 обычных требований, то с интенсивностью Λ1(v1, v2) поступают приоритетные, а с интенсивностью Λ2(v1, v2) —обычные требования. Это означает, что при фиксированных v1 и v2 потоки поступающих приоритетных и обычных требований — независимые пуассоновские с параметрами Λ1 и Λ2 соответственно. В такую модель укладываются, в частности, схемы с бесконечными и конечными источниками требований. Обозначим Λ(v1, v2) = Λ1(v1, v2) + Λ2(v1, v2), pi(v1, v2) = Λi(v1, v2) [Λ(v1, v2)]-1, i = 1, 2. Пусть длительности обслуживания отдельных требований — случайные величины, не зависящие ни от процесса поступления, ни от длительностей обслуживания остальных требований. Обозначим через Bi(x) функции распределения длительностей обслуживания требований i-ro типа, i = 1,2.
Прочитать остальную часть записи »
Пример 1 — модели сложных систем, описываемые как КЛП
Пример 1. КЛП Гнеденко — Коваленко.
Рассмотрим случайный марковский процесс, служащий моделью широкого класса систем массового обслуживания. Состоянием процесса является вектор z переменной размерности, z = (v, zv (1), …, zv(|v|)), где компонента v (основное состояние) принимает значения из конечного или счетного множества N, a zv(j) > 0, j= 1,…,|v|. В промежутках между скачками zv(j) изменяется с постоянной скоростью vv(j). Скачки у этого процесса бывают двух типов. Скачки первого типа (вследствие непрерывного вмешательства случая) происходят с интенсивностью λ(v), зависящей лишь от v. В этом случае после скачка новое основное состояние μ будет случайным с распределением {pvμ}, ∑pvμ=1, зависящим лишь от прежнего основного состояния. Таким образом, при рассматриваемом скачке размерность вектора z может только увеличиться. Новый вектор дополнительных координат z* при этом составляется из старого вектора z" и случайного не зависящего от предыстории процесса z, положительного вектора ξvμ размерности |μ| — |v|, функция распределения которого Hvμ (х (1), …, х (|μ| — |v|), х (j) > 0, зависит только от v и μ. Именно zμ = (zv, ξμ) = (zv(1), …, zv(|v|), ξvμ (1), …, ξvμ(|μ|— |v|)). После такого скачка координаты вектора zμ вновь изменяются с постоянной скоростью vμ.
Прочитать остальную часть записи »
Вывод формулы для КЛП (кусочно-линейных марковских процессов)
Установим теперь для КЛП формулу, аналогичную формуле (1.3). Пусть V(z)—некоторая ограниченная функция, такая, что V(v, zv+vvt), рассматриваемая как функция t при zv+vvt∈Гv, непрерывна и обладает непрерывной справа правой производной. Доопределим V(z) на Z* по непрерывности следующим образом: пусть z* = (v, z*v)∈Z*, и пусть последовательность {ti}i≥1 сходится к 0 и обладает тем свойством, что z*v + vvti∈Гv, i≥1; тогда положим V (z*) = lim V (v, z*v + vvti); если же последовательности, обладающей указанным свойством, не существует, то в таких точках z* функцию V доопределим произвольно — такая точка z* недостижима. Обозначим класс полученных функций DА и будем предполагать, что V∈DА.
Прочитать остальную часть записи »
Кусочно-линейные марковские процессы с непрерывным временем
Один из способов анализа немарковского процесса состоит в расширении пространства его состояний, для того, чтобы включить в понятие состояния всю ту информацию о предыстории исходного процесса, которой полностью определяется его будущее течение. Иногда такая информация может быть задана в виде конечномерного вектора. Именно такому способу анализа немарковских процессов и обязана своим возникновением схема кусочно-линейных марковских процессов (КЛП).
Прочитать остальную часть записи »
Система обслуживания с относительным приоритетом
Система обслуживания с относительным приоритетом. Дадим теперь пример системы массового обслуживания, описание которой хотя и укладывается в схему (1.5), но не укладывается в схему кусочно-линейных преобразований, определенных в примере 5.
Пусть в однолинейную систему поступает N рекуррентных потоков требований, т. е. в k-м потоке требования поступают через случайные промежутки времени, являющиеся независимыми одинаково распределенными случайными величинами с функцией распределения Нk(х), 0 ≤ х < ∞. Прочитать остальную часть записи »
Леммы — модели систем с дискретным временем
Лемма 1. Если S1 — ς(ϑ)-оператор, S1 : ϑ→ψ, S2ς(ψ)-оператор, S2:ψ→β, то оператор S = S2S1 является ς(ϑ)-оператором.
Прочитать остальную часть записи »