Образовательный блог – всё для учебы

Пример схемы резервирования с конечным временем переключения элементов.

Рассмотрим следующую систему (рис. 5), состоящую из n идентичных элементов.

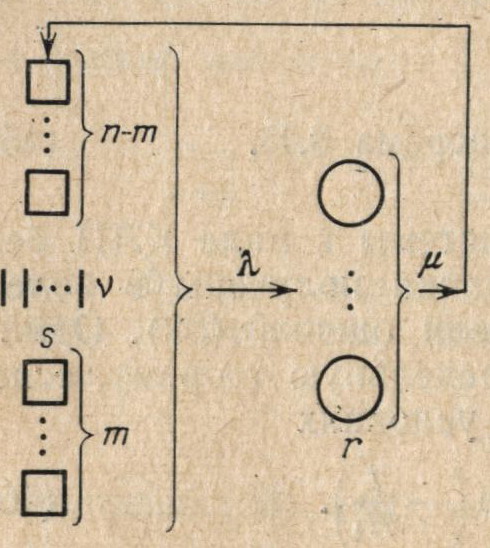
В полностью исправном состоянии в системе имеются m элементов, находящихся на рабочих местах («рабочих» элементов), n—m элементов, находящихся в нагруженном (горячем) резерве («резервных» элементов). При выходе какого-либо рабочего элемента из строя он мгновенно поступает на одно из r ремонтных мест, r ? n, если имеется свободное, либо становится в очередь на ремонт. Замена отказавших элементов происходит следующим образом. Если в наличии есть хотя бы один резервный элемент, а общее количество работающих и подключаемых элементов меньше m, то этот резервный элемент немедленно начинает переключаться с резервного места на рабочее. Время переключения каждого отдельного элемента — случайная величина с функцией распределения 1—е^-vx. Дополнительно предположим, что число одновременно переключаемых элементов не может превышать некоторого числа s. Элементы системы являются ненадежными и могут отказывать как на рабочих местах, так и в резерве и в состоянии переключения. Будем называть элемент исправным, если он находится в одном из этих трех состояний: рабочем, резервном и переключения. Время пребывания элемента в исправном состоянии является, по предположению, случайной величиной с функцией распределения 1-е^-?x. Время ремонта отдельного элемента также случайно и имеет функцию распределения 1-е^-?x. Все перечисленные случайные величины независимы в совокупности.

Если за состояние системы выбрать пару z_t = (?_t(1), ?_t(2)), где ?_t(1) —число рабочих элементов, а ?_t(2) — число неисправных элементов в момент t, то, очевидно, z_t — однородный марковский процесс с конечным числом состояний. Множество возможных состояний Z системы определяется неравенствами:

0 ? ?(1) ? m, 0 ? ?(1) + ?(2) ? n.

Будем считать, что отказ системы наступает тогда, когда
нет ни одного работающего элемента, т. е. выберем в качестве множества «рабочих» состояний {z = (?(1), ?(2)): ?(1) ? 0}.

Прежде чем анализировать данную задачу, приведем следующий весьма полезный факт, который может использоваться и в более общих ситуациях.

Пусть z_t — однородный марковский процесс с непрерывным временем и конечным множеством состояний Z, причем все состояния сообщающиеся. Пусть Q—собственное подмножество Z. Обозначим через T_z, z?Q, среднее время выхода процесса с начальным состоянием z из подмножества Q. В сделанных предположениях эти величины существуют и конечны. Пусть, ?_{?, ?} — интенсивность перехода рассматриваемого процесса из состояния ? в состояние ?, а ?_? = ? ?_{?, ?}. Тогда величины T_z
удовлетворяют следующим уравнениям:

T_? = ? ?_?^-1(1 + ? ?_{?, ?}T_?). (47):

Мы имеем дело с высоконадежным случаем: ? ? ?, ? ? v. Конкретные оценки приводиться не будут, но они могут быть получены.

1. Примеры 1 и 2 моделей с дискретным временем
2. Ограниченность для процессов с дискретным временем
3. Кусочно-линейные марковские процессы с непрерывным временем
4. Достижимость для процессов с дискретным временем
5. Пример 3 и 4 моделей систем с дискретным временем
6. Марковские процессы с дискретным временем
7. Леммы – модели систем с дискретным временем
8. Оптимизация надежности объекта как системы элементов
9. Постановка задачи оценки распределения момента первого достижения
10. Свойство регулярности. Необрывающиеся процессы
11. Принципиальная схема электрофильтра и степень очистки газов
12. Пример – ненагруженное дублирование с восстановлением
13. Общие принципы расчета надежности структурных схем электростанций
14. Подсчет числа размещений, перестановок, сочетаний без повторов и с повторами
15. Принципиальная схема КУ
16. Производящие функции для размещений с повторениями с ограничениями и без ограничений на число повторов
17. Постановка задачи устойчивости предельных режимов