Примеры устойчивости предельных режимов
Во всех приводимых ниже примерах равномерная независимость процесса от начального состояния проверяется путем не слишком сложного построения конкретных множеств ВN для которых выполнены свойства (2.24) и (2.25).
Пример 1. Многолинейная система обслуживания с ожиданием. Рассмотрим процесс zt введенный в примере 1.2.3:
zt+1 = R(zt + ηte — θtI)+. (1)
Как следует из результатов, изложенных в примере 1.2.5, данный процесс порожден кусочно-линейными преобразованиями. Вид образующих приведен в конце примера 1.2.5. Характеристическое множество для данного процесса имеет вид {0, z(1), …, z(N)}, где z(i), i = 1, …, N, — компоненты вектора z .
Если
Мηt < N×Мθt, (2)
то, как следует из результатов (см. примеры в других постах), процесс zt ограничен в среднем по времени. При условии
Р{θt > ηt} > 0 (3)
у процесса zt, как нетрудно видеть, точка z = (0, …, 0) является возвратной, и в этом случае процесс zt является регенерирующим. Если В(х) = Р {ηt ≤ x} Н(х) = Р {θt ≤ x}, х ≥ 0, то условие (3) можно записать в виде
∫B(x)H(dx) > 0. (4)
Однако можно показать, что для равномерной независимости процесса zt от начального состояния достаточно выполнения лишь условия (2).
Рассмотрим функцию
v(z) = ||z|| = max |z(i)|. (5)
Но для любого набора функций (lk(1)0, …, lk(N)0) из характеристического множества
v(lk(1)0(z), …, lk(N)0(z)) ≤ max |z(i)|.
В условиях (2) у процессов zt, zt* существуют финальные распределения Q, Q* соответственно. Следовательно, все условия теоремы выполнены, при этом имеет место слабая устойчивость в пределе.
Пример 2. Многофазная система обслуживания с ожиданием перед каждой фазой. Система описана в примере 1.2.4 рекуррентными соотношениями (1.2.8). В примере 1.2.5 показано, что данный процесс порожден кусочно-линейными преобразованиями, и дан вид образующих. Поскольку характеристическое множество имеет тот же вид, что и в предыдущем примере, то с помощью функции (5) при выполнении условий равномерной независимости от начального состояния и ограниченности в среднем по времени доказывается устойчивость процесса zt в среднем по времени.
Нетрудно понять, что условием равномерной независимости от начального состояния является следующее:
min Р{θt > ηt(j)} > 0,
или
min ∫Bj(х)Н(dx) > 0. (6)
С другой стороны, условие
Мθt > max Мηt(j) (7)
гарантирует ограниченность в среднем по времени. Но из условия (7) следует выполнение неравенства (6). Поэтому, если выполнено (7), то у процессов zt, zt* существуют финальные распределения Q, Q* соответственно, и имеет место слабая устойчивость в пределе.
Пример 3. Многолинейно-многофазная система. Рассмотрим систему, схематически изображенную на рис. 8 и состоящую из N фаз обслуживания.
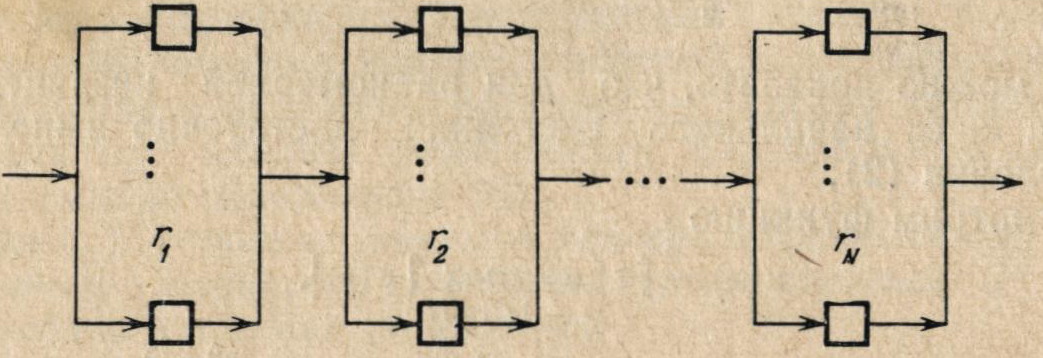
Рис 8.
Перед каждой фазой допускается неограниченная очередь. Длительности обслуживания различных требований независимы в совокупности и Bi(x) их (общая) функция распределения на приборах, входящих в i-ю фазу, 1 ≤ i ≤ N. Всего i-я фаза состоит из ri параллельно работающих приборов. Обозначим М0 = 0, Mi = ∑rj, 1 ≤ i ≤ N, М = МN. Состояние системы будем характеризовать M-мерным вектором z = (z(1), …, z(M)) и рассмотрим систему в последовательные моменты поступления требований. Таким образом, zt — состояние процесса в момент поступления t-го требования. Определим компоненты вектора состояния. Для этого сначала будем считать, что t > М. В дальнейшем покажем, что это ограничение несущественно.
Пусть Tt — множество требований, имеющих номера {1, …, t—1}. Обозначим через Т1t⊂Тt подмножество из r1 требований (входящих в множество Tt), которые последними обслужились (или обслужатся) на первой фазе, т. е. исходное множество Тt переупорядочивается в соответствии с моментами ухода требований с первой фазы, а множество Т1t составляют последние r1 требований. Аналогично определим подмножество Тit⊂Тt из r, требований, которые последними обслужились на 1-й фазе, 2 ≤ i ≤ N. Внутри каждой из групп Тit требования упорядочим в порядке их ухода с i-й фазы. Будем считать, что в каждый рассматриваемый момент t требования упорядочены в соответствии с описанным выше правилом. Положим координату zt(s) при Mt-1 < s ≤ Mi равной разности между моментом ухода s-ro требования (принадлежащего множеству Тit) с i-й фазы и моментом поступления в систему t-ro требования.
Пусть θt — интервал между моментами поступления t-го и (t + 1)-го требований, {ηt(i} — последовательность длительностей обслуживания требований на i-й фазе.
Соотношения имеют смысл не только при t > М, но и при всех t ≥ 0. Приведенная выше интерпретация координат сохраняется и в общем случае. Если при этом к моменту t = 0 в системе было меньше, чем М требований, то данную интерпретацию легко сохранить, предположив, например, что в начальный момент времени в системе было достаточное число фиктивных требований, время обслуживания которых на всех фазах равно нулю.