Рассмотрим класс алгоритмов, которые основаны на квадратичной аппроксимации минимизируемой функции Q (х) в Δ-окрестности каждого приближения x^r разложением в ряд Тейлора. В связи с тем, что для определения очередного приращения Δ^r эти алгоритмы требуют вычисления первых и вторых производных функций Q (х), они получили название методов второго порядка.

В том случае, когда гессиан G (х^r) является положительно определенной матрицей, приращение Δ^r, обеспечивающее наибольшую скорость уменьшения функции Q (х) при постоянном значении квадратичной части разложения в ряду Тейлора, определяется из решения экстремальной задачи:

min (∇Q^T(х^r, Δ) при условии, что Δ^TG(х^rΔ = К. (5.45)

Оптимальным решением задачи (5.45) является вектор

Δ^r = — G^-1(x^r)∇Q(х^r), (5.46)

где G^-1(х^r) — матрица, обратная гессиану, вычисленному в точке х^r.

В тех случаях, когда обращение матрицы G(x^r) может привести к большим ошибкам вычисления в силу того, что ее определитель близок к нулю, приращение Δ^r можно находить из решения системы линейных уравнений:

G(х^r)Δ = — ∇Q(х^r).

Алгоритм F²⁵, основанный на использовании итерационной формулы (5.45), где процедуры выбора длины шага λ_r и направления поиска Sⁱ совмещены и сводятся к вычислению приращения Δ^r по формуле (5.46), является реализацией широко распространенного метода Ньютона. Основная идея этого метода заключается в том, что на каждой итерации осуществляется выбор приращения Δ^r, соответствующего расстоянию до минимального значения квадратичной формы, аппроксимирующей функцию Q (х) в точке x^r (рис. 5.2).

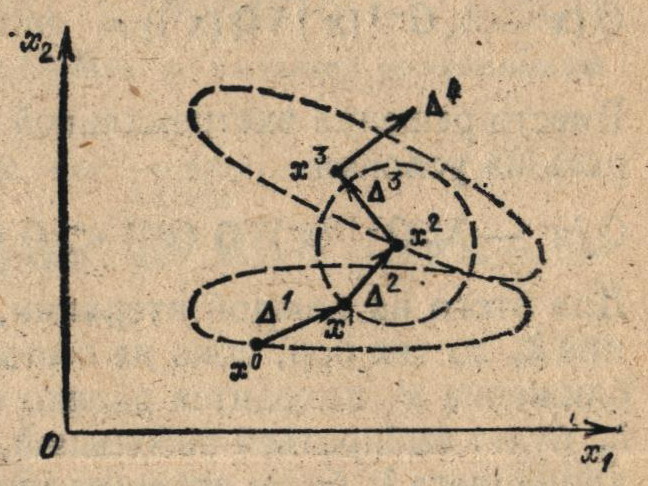
Рис. 5.2. Геометрическая интерпретация метода Ньютона с точки зрения квадратичной аппроксимации функции Q(x) в точках х⁰, x¹ и х² (пунктирные кривые)

При минимизации квадратичной функции Q (х) = х^TAx + b^Tх + a, независимо от значения коэффициента обусловленности матрицы А, метод Ньютона позволяет найти точку минимума х* из любого начального приближения х⁰ за одну итерацию.

Для нелинейной функции Q (х) точка минимума х* не может быть получена за одну итерацию. Однако направление поиска Δ^r из (5.46) значительно ближе к направлению на точку минимума х*, чем антиградиент, что и обеспечивает более высокую скорость сходимости метода Ньютона по сравнению с методом наискорейшего спуска.

Недостатком метода Ньютона является требование, чтобы начальное приближение х⁰ лежало в достаточно малой окрестности точки локального минимума x*. При выполнении этого требования алгоритм обладает квадратичной скоростью сходимости. Однако на практике это условие часто трудно выполнить, в связи с чем при неудачном начальном приближении x⁰ использование метода F²⁵ может привести к расходящемуся процессу.

Для обеспечения сходимости метода Ньютона к точке минимума х* независимо от значения начального приближения х⁰ будем определять приращение Δ^r из выражения

Δ^r = — λ_rG^-1(x^r)∇Q(x^r). (5.49)

где длина шага λ_r является оптимальным решением задачи одномерного поиска:

Q(x^r — λ_rG^-1(x^r)∇Q(x^r) = min Q(x^r — λG^-1(x^r)∇Q(x^r). (5.50)

Вместо решения экстремальной задачи (5.50) параметр λ_r, можно выбирать из условия

Q(x^r — λ_rG^-1(x^r)∇Q(x^r) < Q (х^r). (5.51)

Для этого на каждой итерации, начиная о λ_r = 1, уменьшают значение λ_r до тех пор, пока не выполнится неравенство (5.51). Если приближение x^r находится далеко от точки минимума х*, то длина шага λ_r, будет выбираться небольшой, при приближении точки х^r к точке х* длина шага λ_r будет стремиться к единице.

Алгоритм F²⁶, основанный на итерационной формуле (5.45), в которой приращение Δ^r определяется выражением (5.49), а длина шага λ_r — условием (5.50) или (5.51), называется методом Ньютона с регулируемым шагом.

Общим недостатком методов F²⁵ и F²⁶ является то, что в них процесс поиска минимума х* может расходиться, если гессиан G(х^r) не является положительно-определенной матрицей.

Для обеспечения требования, чтобы на каждой итерации гессиан G(х^r) был положительно-определенной матрицей, можно использовать следующий прием:

G*(x^r) = G (х^r) + ρI, (5.52)

где I — единичная матрица; ρ — достаточно большое положительное число. Тогда существует ортогональная матрица V такая, что

V^TG*(x^r)V = V^TG(х^r)V + ρI = D(х^r) + ρI. (5.53)

где D(х^r) — диагональная матрица, элементы которой равны собственным значениям гессиана G (х^r).

Алгоритм F²⁷, реализующий метод Ньютона с регулируемым шагом, в котором используется преобразованная матрица G*(x^r‘) из (5.52), называется модифицированным методом Ньютона.

Процедура поиска точки минимума х* по алгоритму F²⁷ считается законченной, если выполняется условие:

l|∇Q(x^r+1)|| ≤ ε.

Общим недостатком алгоритмов F²⁶ и F²⁷, реализующих различные модификации метода Ньютона F²⁵, является то, что в них требуется вычислять матрицу вторых производных G (х^r) и осуществлять обращение этой матрицы. В связи с этим рассмотрим класс алгоритмов, обладающих, так же как и метод Ньютона, квадратичной скоростью сходимости, но не требующих вычисления матриц G(x^r) и G^-1(х^r). Алгоритмы этого класса основаны на формировании специальным образом последовательности матриц {Н_r}. Эта последовательность обладает тем свойством, что каждый ее элемент аппроксимирует на r-м шаге соответствующий элемент матрицы G^-1(х^r), но вычисляется только на основании информации о значениях первых производных функций Q (х).

Как было показано выше, для квадратичной функции метод Ньютона F²⁵ позволяет получить точку минимума х* из любого начального приближения (например, х^r+1 и х^r) за одну итерацию.

Гессиан квадратичной функции является симметрической матрицей (A = A^T‘), поэтому потребуем, чтобы каждая из матриц Н_r также была симметрической. Для того чтобы сохранить это свойство у матрицы H_r+1, необходимо, чтобы для поправки ΔH_r выполнялось условие

ΔH_r = ΔH_r^T. (5.64)

В том случае, когда алгоритм поиска образует релаксационную последовательность, говорят, что он устойчив (сходится к точке минимума x*). На практике условие, обеспечивающее устойчивость поиска, выполняется на каждой итерации лишь тогда, когда длина шага Δ_r определяется из решения одномерной задачи оптимизации min Q{x^r — λH_r∇Q(x^r) точно. В противном случае процесс поиска точки минимума x* может стать расходящимся. Поэтому после проведения n итераций по алгоритму процесс поиска целесообразно «обновлять» («восстанавливать»), т. е. начать сначала, приняв в качестве H₀ единичную матрицу I, а в качестве начального приближения х⁰— точку хⁿ⁺¹.

Теоретическое сравнение методов сопряженных направлений и квазиньютоновских методов минимизаций показывает, что при минимизации квадратичных функций они полностью совпадают. При минимизации нелинейных «овражных» функций квазиньютоновские методы оказываются предпочтительнее методов сопряженных направлений, если «дно оврага» не очень извилистое. Однако их программная реализация требует больших затрат оперативной памяти, чем при реализации методов сопряженных направлений.

Комментарии запрещены.