Рассмотрим обобщение метода F²¹ поиска точки глобального минимума произвольной кривой с помощью стохастического автомата на случай многопараметрических положительных функций Q (х).

Каждый интервал [0, c_i] изменения i-й переменной разделим на K_i отрезков равной длины

ω_i = c_i/K_i, i =1, 2, …, n. (6.35)

Этим самым n-мерный параллелепипед D_x = {х|, 0 ≤ x_i ≤ c_i, i = 1, …, n} разобьется, на

M = ∏K_i

подобластей одинакового объема

V_i = ∏ω_i, l = 1, 2, …, М. (6.36)

Каждую подобласть V_i будем характеризовать центральной точкой x^l с компонентами

x_i^j = ω_i(j — 1/2), i = 1, 2, …, n; j = 1, 2, …, K_i. (6.37)

Индекс l для вектора x^l определяется с помощью следующего выражения:

l = j(x₁^j) + ∑({j(x_r^j — 1} ∏K_t), (6.37)

где j(x₁^j) — верхний индекс компоненты x₂^j, i = 1, 2, …, n.

Например, для двумерного случая со значениями K₁ = 3 и К₂ = 2 нумерация подобластей V_l определяется по формуле (рис. 6.8, а):

l = j(x₁^j) + [j(x₂^j) — 1],

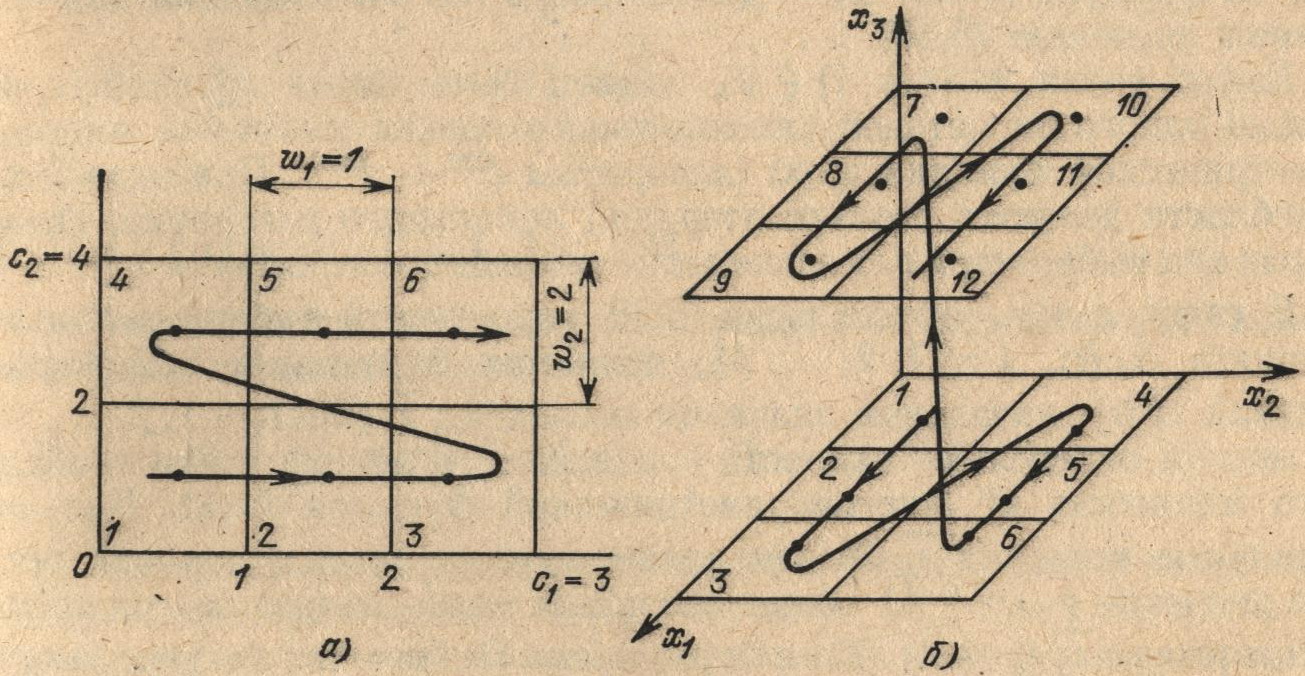
Рис. 6.8. Нумерация подобластей V_l, полученная при разбиении параллелепипеда D на области одинакового объема для n=2 (а) и n=3 (б).

а для трехмерного случая K₁ = 3 и K₂ = K₃ = 2 — по формуле (рис. 6.8, б):

l = j(x₁^j) + [j(х₂^j) — 1]3 + [j(x₃^j) — 1]6.

Полученное разбиение параллелепипеда D_x дает возможность поставить в соответствие каждой подобласти одинакового объема V_l состояние S(r) стохастического автомата и вероятность р_l(r) выбора им на r-м шаге 1-й подобласти для проведения в ней очередного испытания x(r). Структура стохастического автомата изменяется после каждой итерации согласно соотношениям, рассмотренным в посте про поиск глобального минимума кривой с помощью стохастических автоматов;

p_l(r+1) = z_l*(r+1)/(∑z_i*(r+1)), l = 1, 2, …, M;
z_k*(r+1) = αz_k*(r) + (1 — α)z_k(r+1), 0 < α < 1; z_j*(r+1) = αz_j*(r), j = 1, 2, …, M, j ≠ k;
z_k(r+1) = [1/Q(x'(r+1))]^γ, (6.38)

где k — номер k-й подобласти объемом V_k, в которой на (r + 1)-м шаге было проведено испытание; Q(x'(r + 1)) — значение минимизируемой функции, вычисленное на (r + 1)-м шаге в точке х'(r + 1), которая принадлежит «исследуемой к-й подобласти.

Испытание в k-й подобласти осуществляется в точке х'(r + 1)∈V_k, компоненты которой выбираются по равновероятному закону распределения f = 1/ω_k из подынтервала

х_i^j(k) — ω_i/2 ≤ x_i‘(r + 1) ≤ х_i^j(k) + ω_i/2, k= 1, 2, …, n,

где х_i^j(k) — компонента центральной точки k-й подобласти, вычисляемая по формуле (6.36), ω_i — длина ребра по i-й координатной оси, равная значению (6.35).

Выбор точки х'(r + 1)∈V_k может быть также проведен с помощью одного из методов унимодального поиска минимума многопараметрической функции Q (х). При этом в k-й подобласти делается столько итераций локального алгоритма, сколько раз она выбирается для проведения очередного испытания х(r + 1).

В связи с тем, что согласно (6.38) вероятности выбора состояний автомата S_i(r), i = 1, 2, …, М, являются функциями выборочных средних z_i*(r), начальные значения последних z_i*(0), i = 1, 2, …, М, во многом определяют скорость и надежность поиска точки глобального минимума x* многопараметрической функции Q (х). Большие начальные значения z_i*(0) замедляют процесс поиска, так как текущее значение z_k(r + 1) может оказаться очень малым по сравнению со значением z_k*(г + 1). Но в то же время назначение больших значений z_i*(0) приводит к тому, что в процессе поиска испытания проводятся в большем числе различных подобластей, тем самым повышая вероятность локализации точки глобального минимума. Малые начальные значения z_i*(0) повышают скорость поиска, но могут привести к неправильному определению подобласти, содержащей точку глобального минимума х*. Поэтому в качестве начальных значений z_i(xⁱ) можно рекомендовать значения z_i(хⁱ), вычисленные в центральных точках xⁱ каждой из подобластей объемом V_i:

z_i*(0) = [1/Q(xⁱ)]^γ, i=1,2,…,M.

Кроме ускорения процесса поиска такой выбор начальных значений z_i(0) повышает надежность локализации точки глобального минимума, так как нельзя правильно судить о наличии в i-й подобласти точки минимума x*, не проведя в ней хотя бы одного испытания.

Алгоритм, реализующий многомерный поиск глобального минимума с помощью стохастического автомата, сводится к следующей последовательности действий.

1. Для каждой переменной x_i задается число равных отрезков K_i, на которое разбивается интервал [0, c_i] и вычисляются параметры

ω_i = c_i/K_i i = 1,2, …, n.

2. Определяются число подобластей, на которые разбивается область D_x = {х|0 ≤ x_i ≤ c_i, i = 1, 2, …, n},

M = ∏K_i

и координаты центральных точек х^l для каждой подобласти V_l, l = 1, 2, …, M:

x_i^j = ω_i(j — 1/2), i = 1, 2, …, n; j = 1, 2, …, K_i.

3. В центральных точках х^l каждой подобласти V_l, где номер подобласти определяется по формуле

l = j(x₁^j) + ∑({j(x_r^j — 1}∏K_t),

вычисляется

z_l(0) = [1/Q(x^l)]^γ, l = 1, 2, …, M.

4. Вычисляется начальное распределение вероятностей выбора
состояний стохастического автомата

p_l (0) = z_l*(0)/∑z_k*(0), l = 1, 2, …, М.

5. Интервал [0, 1] разбивается на М отрезков, длина каждого из которых пропорциональна вероятности р_i(r), l= 1,2, …, М (на первой итерации r = 0). По равновероятному закону выбирается число ξ∈[0, 1]. Подобласть V_k, в которой необходимо провести очередное испытание на (r + 1)-й итерации, соответствует номеру k-го подынтервала единичного отрезка, содержащего, число ξ.

6. По номеру к определяются вторые индексы j_i(k) центральной точки x^k подобласти V_k и проводится вычисление функции Q (х) в точке х'(k), каждая компонента которой выбирается по равновероятному закону распределения f= 1/ω_i.

7. Пересчитываются, вероятности выбора состояний стохастического автомата.

8. Поиск точки глобального минимума х* заканчивается, если вы-
полняется условие

max p_l(r + 1) > p₀,

где p₀ — заданное положительное число (0 < p₀ ≤ 1). В противном случае принимается r = r + 1 и все вычисления повторяются с п. 5.

Комментарии запрещены.