Образовательный блог – всё для учебы

Многопроцессорные ЭВМ открывают возможность одновременной оценки нескольких независимых значений функции Q (х) путем распараллеливания вычислений. В связи с чем для минимизации унимодальных функций могут быть построены параллельные алгоритмы поиска, в которых на каждом i-м шаге часть испытаний n_i ? N проводится одновременно в заданной совокупности точек х₁, х₂, …, х_n.

Наиболее простыми алгоритмами данного класса являются алгоритмы, реализующие методы пассивного поиска, в которых расположение точек испытаний х_i, i = 1,2,…, N, выбирается заранее до проведения первого вычисления функции Q (х):

а ? х₁ < х₂ < ... < x_N-1 < х_i ? b.

В алгоритме F⁷, реализующем метод равномерного поиска, испытания проводятся в точках, которые определяются путем равномерного деления априорного интервала неопределенности [a, b] на (N + 1)-у часть:

х_i = а + i (b – a)/(N + 1), i = 1, 2, …, N. (3.75)

В полученных точках x_i оцениваются значения функции Q (х), из которых выбирается наименьшее:

Q(x_k)= min Q(x_i).

В связи с унимодальностью функции Q (х) подынтервалы [а, х_k-1] и [х_k+1, b] исключаются, а длина апостериорного интервала неопределенности [х_k-1, х_k+1], содержащего точку минимума х*, определяется выражением:

l_N (F⁷) = b_N — a_N = 2(b- a)/(N + 1). (3.76)

Другим вариантом стратегии пассивного поиска является алгоритм F⁸, реализующий метод равномерного дихотомического поиска, основная идея которого заключается в том, что испытания проводятся парами, которые при четном числе испытаний N = 2m (m ? 1), равномерно располагаются на интервале [а, b] согласно формулам:

x_2i-1= a + i (b — a)/(m + 1), (3.77)

х_2i = x_2i-1 + ?, i = 1, 2, …, m,

где

0 < ? < (b — а)/(m + 1) — число, достаточное для того, чтобы различить, какая из точек в паре лучше по значению функции Q (х). После проведения m пар испытаний апостериорный интервал неопределенности определяется выражением:

l_N (F⁸) = b_N – a_N = (b – a)/(0.5N+1) + ?. (3.7.8)

Недостатком методов F⁷ и F⁸ является то, что в них выбор точек испытаний x_i, i = 1, 2, …, N, осуществляется без учета информации о значениях функции Q (х), вычисленных в этих точках. Этот недостаток устранен в методах блочного поиска, которые сочетают в себе пассивные и последовательные стратегии поиска. При этом N испытаний разделяются на l блоков, в каждом из которых проводится одновременно n_i испытаний, т. е. блок — это совокупность из нескольких испытаний, которые проводятся одновременно. (В частном случае блок может состоять из одного испытания.) Результаты, полученные в (k – 1)-м блоке, становятся известными перед началом проведения испытаний в k-м блоке и определяют стратегию выбора точек очередных испытаний x_i, i = 1, 2, …, n_k, в этом блоке.

Введем следующие обозначения:

x_t,j — расположение точки j-го испытания в t-м блоке (Q_t,j = Q (x_t,j));

x_t,k — точка, обеспечивающая в t-м блоке минимальное значение функции Q (х) среди всех проведенных испытаний;

a_t = x_{t, k-1}; b_t = х_{t, k+1} — границы интервала неопределенности, которые получаются после проведения всех испытаний в t-м блоке.

Для заданного числа испытаний N рассмотрим алгоритм F⁹, реализующий блочную стратегию поиска, которая состоит из l блоков постоянной длины n_i = n, i = 1, 2, …, l. При четном числе испытаний в блоке n = 2m (m ? 1) процедура поиска сводится к следующей последовательности действий.

Испытания в первом блоке (t = 1) одновременно проводятся в точках (рис. 3.10,а).

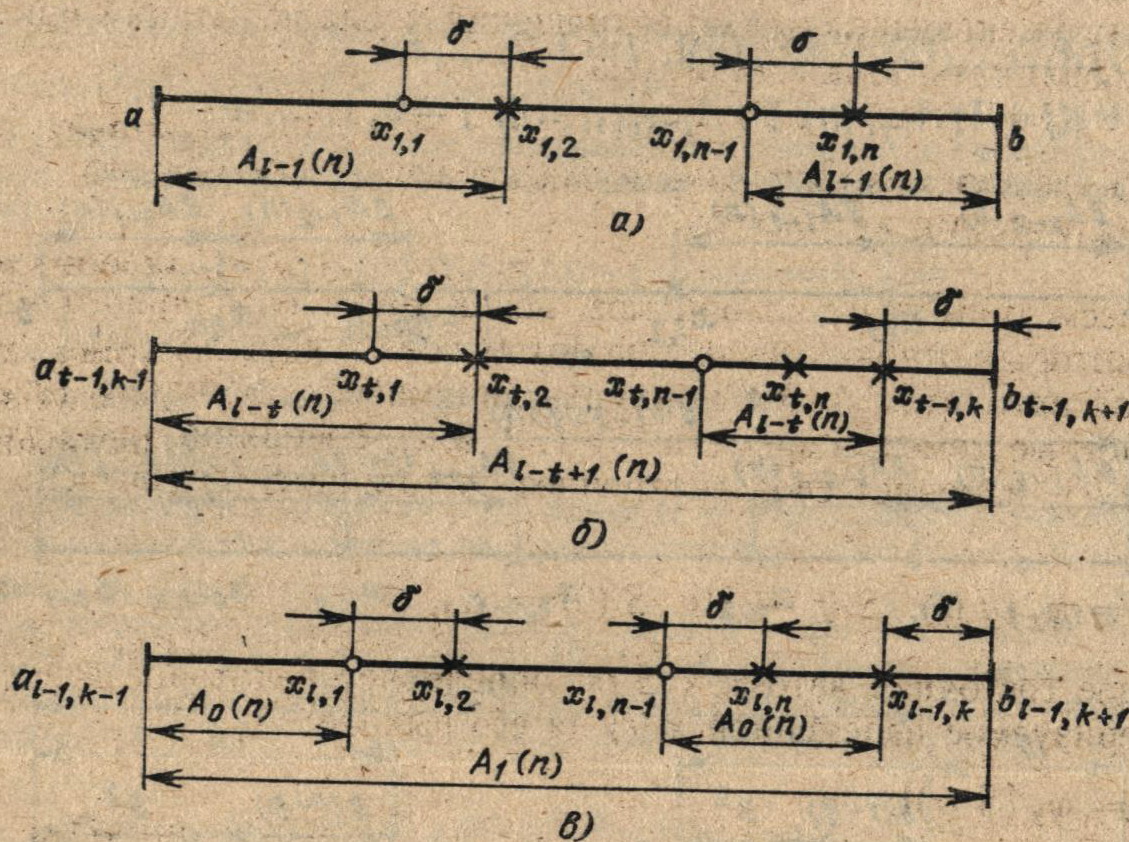
Рис.3.10 Расположение точек испытаний в алгоритме F⁹ при четном числе испытаний в блоке

x_{t, 2j} = jA_l-1, j = 1, 2, …, m; (3.79)
x_{t, 2j+1} = x_{t, 2j} – ?. j = 0, 1, …, m-1.

Здесь А_l (n) = (n+2)/2 A_l-1 (n), А₀ (n) = 1 — числа Авриэла для четных n, первые несколько значений.которых для различных l и n приведены в табл. 3.3.

Таблица 3.3

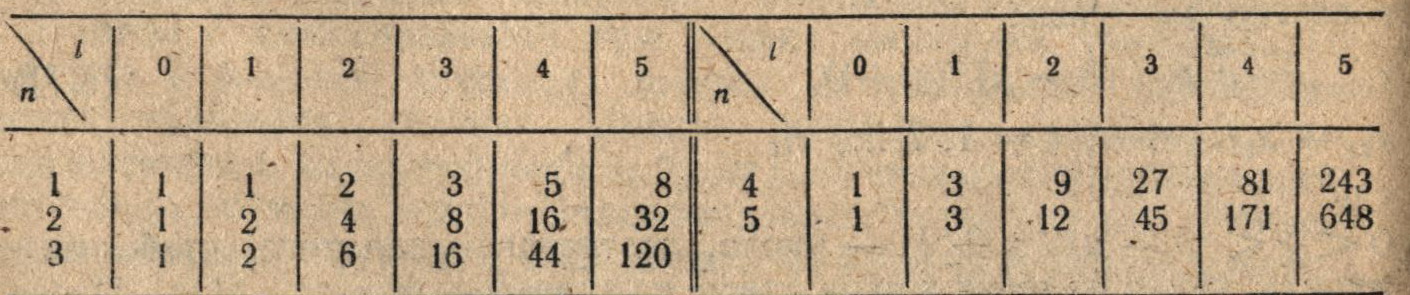
Если длина априорного интервала неопределенности [а, b] не превышает числа Авриэла А_l(n), то алгоритм F⁹ позволяет локализовать точку минимума х* в апостериорном интервале неопределенности [а_N, b_N] единичной длины. Другими словами, длина апостериорного интервала неопределенности определяется выражением:

l_N(F⁹) = b_N – a_N = (b – a)/A_l(n). (3.84)

При l ? 2 и n = 1 делается последовательно l испытаний, так как алгоритм F⁹ состоит из l блоков, в каждом из которых проводится только одно испытание. В этом случае по формулам для чисел Авриэла можем записать

А_l(1) = A_l-1 (1) + A_l-2(1);
A₀(1) = A₁(1) = 1.

Полученные рекуррентные соотношения определяют числа Фибоначчи, следовательно, b_N — a_N = (b — a)/A_l(l) = (b — a)/u_l, т.е. алгоритм F⁹ совпадает с методом Фибоначчи.

При l = 1 и n ? 2 делается одновременно n испытаний, так как алгоритм F⁹ состоит из одного блока, в котором проводится n испытаний. В этом случае по формулам для чисел Авриэла можем записать

А_l(n) = (n+1)/2 для нечетных n;
А_l(n) = (n+2)/2 для нечетных n;

Из полученного выражения для апостериорного интервала неопределенности следует, что при l = 1 Для нечетных n алгоритм F⁹ совпадает с методом F¹, а для четных n — с методом F⁸.

В тех случаях, когда общее число испытаний N = ln постоянно, метод Фибоначчи является более эффективным, чем метод блочного поиска F⁹. Это связано с тем, что при фиксированном числе испытаний в методе F² информация о проведенных испытаниях используется полностью. В методе же блочного поиска F⁹ часть информации о значениях функции Q_t,j, полученных при пассивном поиске внутри t-го блока, не используется при формировании стратегии поиска в (t + 1)-м блоке.

Недостатком метода F⁹, реализующего блочный алгоритм поиска, является то, что число блоков l в нем должно быть задано перед началом поиска. В связи с этим рассмотрим алгоритм F¹⁰, реализующий блочный метод золотого сечения, который лишен этого недостатка.

1. Методы полиномиальной интерполяции
2. Метод Фибоначчи
3. Повышение эффективности унимодального поиска за счет дополнительной информации о минимизируемой функции
4. Поиск минимума унимодальной функции путем сокращения интервала неопределенности
5. Градиентные методы спуска
6. Сведение многомерной задачи оптимизации к задаче одномерного глобального поиска
7. Построение аппроксимирующих моделей минимизируемой функции
8. Метод кусочно-кубической и кусочно-линейной аппроксимации.
9. Квазиньютоновские методы минимизации
10. Геометрическая интерпретация задач поиска и оптимизации
11. Методы-функции и методы-процедуры – синтаксис объявления, реализация методов и варианты вызова методов
12. Постановка задачи поиска и оптимизации проектных решений
13. Обобщение методов оптимальных покрытий на многомерный случай
14. Задачи и методы оптимизации в системах имитационного моделирования
15. Особенности задач поиска и оптимизации проектных решений
16. Виртуальные и динамические методы, замещающие методы
17. Особенности ЭМУС как объектов поиска и оптимизации проектных решений