Стратегия поиска точки глобального минимума х* по алгоритму F²⁰*с помощью автомата Буша—Мостеллера сводится к следующей последовательности действий.

1. Задаются одинаковые значения вероятностей выбора состояний автомата p_j(r) = 1/М, j = 1,2, …, М, и принимается Q_j* = A_∞ для всех j = 1, 2, …, М, где A_∞ — положительное большое число.

2. Согласно распределению вероятностей р (r) генерируется случайное состояние автомата S (к) = S_i, для которого из подынтервала [x_i — ω/2, x_i + ω/2] выбирается (по одному из методов одномерного поиска F¹ — F⁶ или случайно по равновероятному закону распределения f = 1/ω) значение выхода х (r) = x_i (r).

3. В точке x_i (r) проводится испытание Q_i = Q (x_i (r)) и вычисляется параметр Q* = min Q_j*.

4. Определяется реакция среды на действие автомата x_i(r):

y(r+1) = 1, если Q_i ≤ Q*
y(r+1) = 0 — в противном случае.

5. Принимается Q_i* = min (Q_i*, Q (x_i (r))).

6. Если у (r + 1) = 1, то принимается Λ_i(r) = 1 и Λ_j(r) = 0, j= 1, 2, …, M, j ≠ i. При у(r + 1) = 0 значения Λ_j(r) = p_j(r), j = 1, 2, …, М.

7. Формируется новая структура стохастического автомата путем изменения вероятностей выбора состояний S_j, j = 1, 2, …, М:

р(r + 1) = λIр(r) + (1 — λ)(Λ(r) Λ (r) … Λ (r)) р(r), где 0 ≤ λ ≤ 1

8. Все действия повторяются в п. 2 до тех пор, пока о заданной точностью не выполнятся условия целесообразного (4.86) или асимптотически оптимального (4.85) поведения.

В качестве примера на рис. 4.10 приведены гистограммы вероятностей появления выходов автомата p_i(r), i = 1, 2, …. 6, полученные после 25 и 100 шагов поиска, а на рис. 4.11 графики изменения вероятностей p₁(r), р₃(r) и р₆(r) от числа r шагов поиска точки глобального минимума х* функции Q (x) = x/10 + cos x, 2 ≤ x ≤ 11.

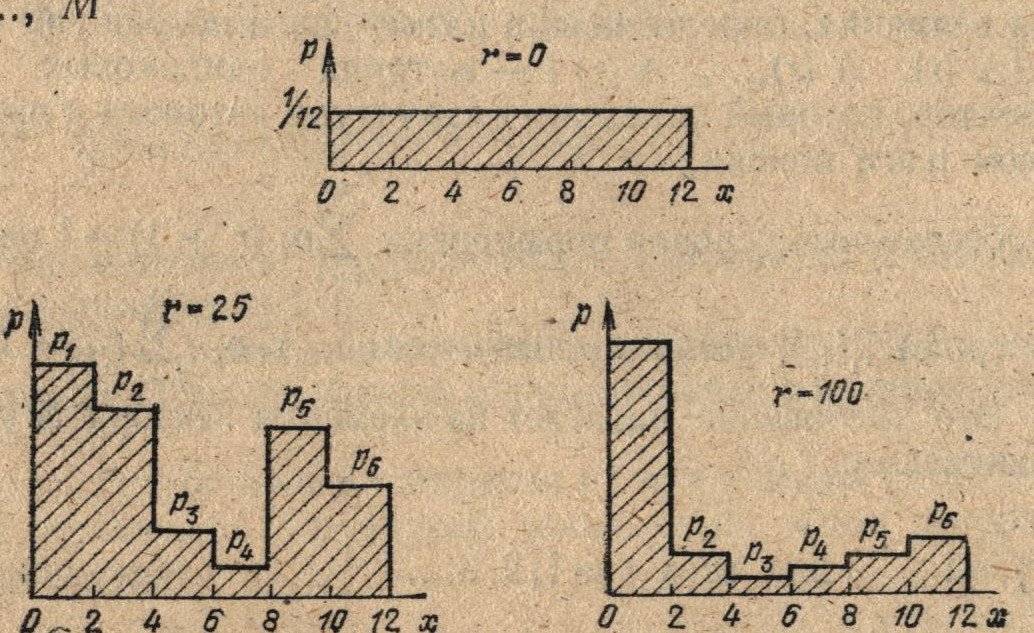
Рис. 4.10. Гистограмма вероятностей появления выходов автомата при минимизации функции Q(x) = x/10 + cos x после r = 0,25 и 100 шагов поиска

Из рис. 4.11 видно, что вероятность p₁(r), которая характеризует подынтервал [0, 2], содержащий точку x*, стремится к единице, а все остальные вероятности p_j(r), j = 2, …, 6, приближаются к нулю.

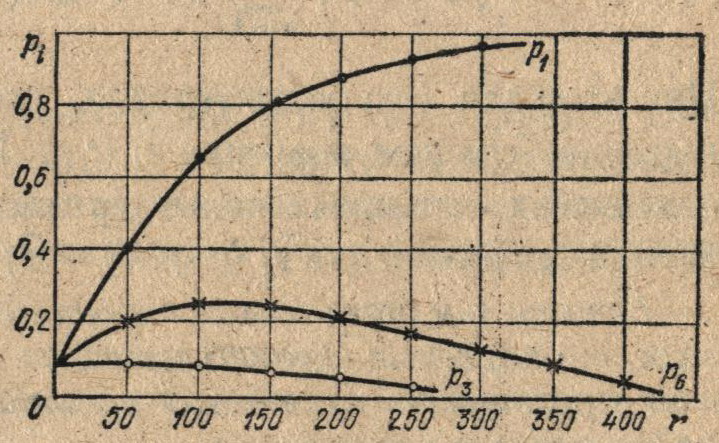
Рис. 4.11. Зависимости вероятностей выбора первого (p₁), третьего (р₃) и шестого (р₆) состояний, автомата Буша—Мостеллера от числа шагов поиска r при минимизации функции Q(x) = x/10 + cos x;

Другой подход К формированию структуры стохастического автомата связан с преобразованием его вектора вероятностей выбора состояний р (r) по информации о средних значениях минимизируемой функции.

В связи с тем, что испытание x_i(r) может быть проведено в любой точке подынтервала [x_i — ω/2, x_i + ω/2], предположим, что истинное минимальное значение Q_i*, характеризующее i-й подынтервал, определяется с некоторой случайной ошибкой ε, которая имеет нулевое среднее значение (М(ξ) = 0) и конечную дисперсию (D{ξ} ≠ 0):

Q(x_i(r)) = Q_i* + ξ. (4.88)

Для того чтобы повысить степень различия в значениях функции Q (х), имеющей несколько локальных минимумов, будем преобразовывать результат каждого испытания следующим образом:

z_i(r)= 1/[Q_i(r)]^γ, (4.89)

где Q_i(r) = Q(х_i(r)) — значение функции Q (х), полученное в момент r для выхода автоматах x(r) = x_j(r); γ ≥ 1 — параметр, определяющий надежность локализации точки глобального минимума х*. При γ = 1 в силу предположения (4.88) значение z_i(r) в i-м подынтервале, не содержащем точку x*, может превысить значение z_j(r) в j-м подынтервале, содержащем точку х*. В то же время выбор значения параметра γ больше единицы приводит к возрастанию обратной величины z_j(r) в j-м подынтервале на большую величину, чем в i-м подынтервале.

Например, пусть Q(x_i(r)) = 1, 0, а Q(х_j(r)) = 1,1. Тогда при γ = 1 имеем Δr = z_j(r) — z_i(r) = 0, 1, а при γ = 16 — Δz = 0,53. Очевидно, что для равновероятных ошибок ξ наилучшей оценкой после проведения k испытаний в i-м подынтервале будет среднее арифметическое значение, которое, учитывая (4.88), можно записать так

M{Q(x_i(r))} = Q_i* + 1/k ∑ ξ(r).

Действительно, так как при r → ∞ математическое ожидание ошибки М{ξ} = 1/k ∑ ξ(r) стремится к нулю, то M{Q (х_i(r))} будет стремиться к истинному минимальному значению Q*. Поэтому в дальнейшем для каждого k-гo испытания, проводимого в t-м подынтервале, будем оценивать среднее значение функции (4.89):

z_i*(k) = 1/k ∑z_i(r). (4.90)

где к — общее число испытаний, проведенных в i-м подынтервале. Из уравнения (4.90) видно, что с ростом числа испытаний к влияние новой информации z_i(k) падает, поскольку вес ее по сравнению о более ранними испытаниями убывает.

В процессе поиска точки глобального минимума х* среда (минимизируемая функция Q(x)) на каждом r-м шаге воздействует на автомат значением z_i(r), изменяя его структуру путем перераспределения вероятностей выбора состояния автомата

p_j (r+1) = z_j(r+1)/∑z_k(r+1), j=1,2,…, M

Рассмотренная модель стохастического автомата обладает асимптотически-оптимальным поведением, если в процессе поиска средние значения z_k(r) вычисляются правильно для каждого из подынтервалов [x_i — ω/2, x_i + ω/2]. Это требование можно выполнить за счет соответствующего выбора значения параметра γ.

Комментарии запрещены.