Пусть минимизируемая функция Q (х) зависит от небольшого числа переменных (n ≤ 3). В этом случае для решения задачи поиска глобального минимума x* непрерывной функции Q (х), определенной в n-мерном гиперпараллелепипеде D_x = {x|a_i ≤ x_i ≤ b_i , i = 1, 2,…, n}

min Q(x₁, x₂, …, x_n), (6.1)

можно использовать алгоритм F³⁴, реализующий метод многошаговой редукции размерности. Основная идея этого метода состоит в том, что исходная задача (6.1) сводится к последовательности «вложенных одна в другую» одномерных задач глобальной минимизации:

min Q(x) = min min … min Q(x₁, …, x_n). (6.2)

Например, для функции трех переменных (n=3) можно записать следующим образом:

min Q(x₁, x₂, x₃) = min Q₁(x₁), (6.3)

Из (6.3) следует, что решение исходной задачи эквивалентно решению задачи минимизации функции одного переменного Q₁(х₁). Вычисление значения функции Q₁(х₁) для фиксированного значения x₁ сводится к решению задачи одномерной минимизации функции Q₂(x₁, х₂) по переменной х₂, а вычисление значения функции Q₂(x₁, x₂) для фиксированных значений переменных х₁ и х₂ — к решению задачи одномерной минимизации исходной функции по переменной x₃.

Таким образом, локализация точки глобального минимума х* многопараметрической функции Q (х) может быть осуществлена с помощью одного из методов одномерного глобального поиска в сочетании со схемой многошаговой редукции (6.2).

Если через N_k обозначить число испытаний, необходимое для отыскания на интервале [а_k, b_k] точки глобального минимума одномерной
функции Q_k(x₁, …, x_k) с заданной точностью ε_k (при фиксированных
значениях переменных x₁, …, x_k-1), то общие затраты на решение задачи (6.1) будут равны

N = ∏N_k

При одинаковом числе испытаний при одномерном поиске N_k = A, k = — 1, …, n, при увеличении размерности исходной задачи общие затраты на поиск будут расти экспоненциально

N = Аⁿ.

Поэтому многошаговая схема редукции (6.2) становится малоэффективной при большом числе переменных.

Другим недостатком алгоритма является то, что точность ε_i решения каждой «вложенной» одномерной задачи минимизации должна быть задана заранее. Если значения этих точностей (ε₁, …, ε_n) окажутся недостаточными при оценке конечного результата, то решение исходной задачи по схеме (6.2) придется повторить заново с меньшими значениями ε_i, i = 1, 2, …, n. Если значения точностей заданы слишком! высокими, то решение исходной задачи (6.1) может прерваться в связи с тем, что исчерпано допустимое число испытаний N. В этом случае полученное приближение

Q(x^k) = min Q(xⁱ)

будет соответствовать оценке минимума функции Q(х) в некоторой подобласти множества D_x. Причем может оказаться, что в значительной части области испытания не проводились, хотя в другой ее части определены минимальные значения некоторых из функций Q_k(x₁,…, x_k-1) с заданными точностями ε_k.

Размерность задачи многомерной минимизации (6.1) может быть повышена до 5—7 переменных за счет использования алгоритма F³⁵, основанного на повторении развертки (кривой Пеано), которая отображает отрезок [0, 1] вещественной оси в гиперпараллелепипед D_x. При этом осуществляется построение однозначного и непрерывного отображения х(v), которое для любой точки v∈[0,1] позволяет получить точку х(v) = (x₁(v), …, x_n(v))∈D_x:

min Q(x₁, …, x_n) = min g(v). (6.4)

Таким образом, решение исходной задачи (6.1) эквивалентно поиску точки минимума v* одномерной функции g(v) = Q(x₁(v), …, x_n(v)) с помощью одного из методов одномерного глобального поиска.

В качестве отображения х(v) рассмотрим схему построения кривой Пеано, предложенную Гильбертом и программно реализованную в работе.

Пусть область D_x при помощи линейного преобразования

y_i = [2x_i — b_i — а_i]/2 (b_i — a_ii), i =1, 2, …, n,

приведена к n-мерному гиперкубу с единичными ребрами:

D_y= {у| — 0,5 ≤ y_i ≤ 0,5, i = 1,2, …, n}. (6.5)

Гиперкуб (6.5) разбивается координатными плоскостями на 2² гиперкубов первого разбиения (m = 1) с длиной ребра, равной 1/2. Полученные гиперкубы нумеруются числами z₁ от 0 до (2ⁿ — 1) таким образом, чтобы гиперкубы с номерами, различающимися на единицу, имели общую грань. Условимся обозначать гиперкубы первого разбиения через D(z₁), где z₁ = 2^k — 1, k = 0, 1, …, n. Тогда смежные гиперкубы D(z₁) и D(z₁ + 1) имеют общую грань, если их центры различаются только одной координатой. Первое разбиение гиперкуба D_y для двумерного случая показано на рис. 6.1, а.

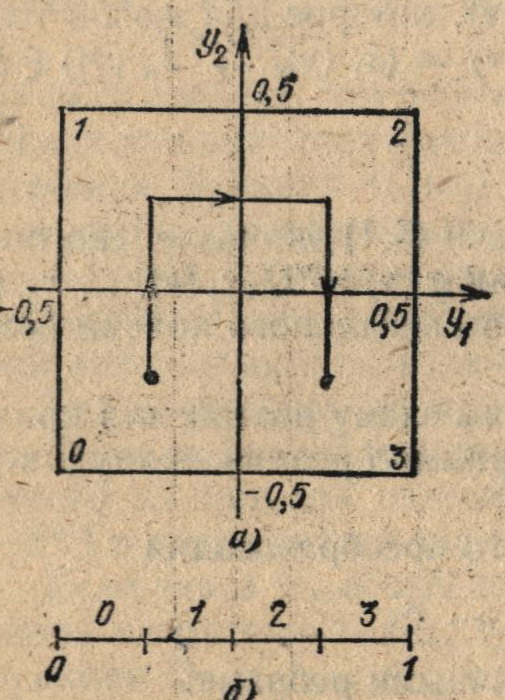
Рис. 6.1. Первое разбиение гиперкуба D_y(a) и отрезка [0, 1] (б)

Далее каждый гиперкуб первого разбиения D(z₁), в свою очередь, также разбивается плоскостями, параллельными координатным осям и проходящими через его центр, на 2ⁿ гиперкубов второго разбиения (m = 2) с длиной ребра равной 1/4. Нумерация полученных гиперкубов проводится по тому же принципу, что и нумерация гиперкубов первого разбиения, с тем отличием, что нулевой гиперкуб второго разбиения, входящий в D(z₁), должен иметь общую грань с (2ⁿ — 1)-м гиперкубом второго разбиения, входящим в D(z₁ — 1). Гиперкубы второго разбиения условимся обозначать D(z₁, z₂), где z₂ = 2^k, k = 0,1,…, n, являются номерами гиперкубов второго разбиения, входящих в D(z₁). Продолжая указанный процесс, можно получить гиперкубы любого s-ro разбиения (m = s) с длиной ребра (1/2)^s которые условимся обозначать D(z₁, …, z_s). Для обеспечения непрерывности строящегося отображения у(v) необходимо, чтобы при нумерации гиперкубов (j + 1)-го разбиения смежные гиперкубы имели общую грань, а нулевой гиперкуб (j + 1)-го разбиения, входящий D(z₁, …, z_j-1, z_j), должен иметь общую грань с (2ⁿ — 1)-м гиперкубом, входящим в D(z₁, …, z_j-2, z_j-1).

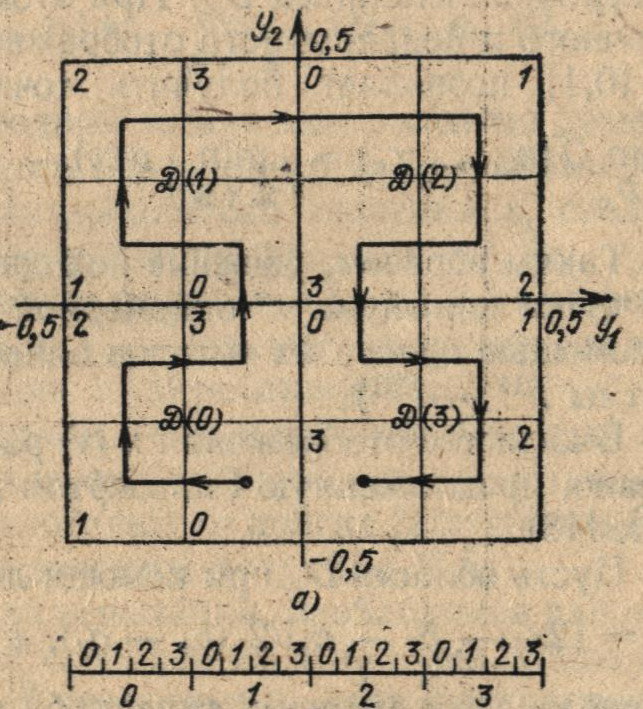
Рис. 6.2. Второе разбиение (m = 2) гиперкуба D_y(а) и отрезка [0,1] (б)

На рис. 6.2а для двумерного случая приведены гиперкубы второго и третьего разбиения с соответствующей введенным условиям нумерацией.

Теперь рассмотрим процесс деления отрезка [0,1] на 2ⁿ равных частей, каждая из которых, в свою очередь, также делится на 2ⁿ равных частей и т. д. При этом интервалы каждого j-го разбиения, длина которых равна (1/2)^jn, нумеруются слева направо числами z_j = 2^k — 1, k = 0, 1, …, n, и обозначаются через Δ(z₁, …, z_j). Например, Δ(z₁, z₂, z₃) означает интервал третьего разбиения с номером z₃, входящий в интервал второго разбиения с номером z₂, который, в свою очередь, входит в интервал первого разбиения с номером z₁. После проведения
s-ro разбиения длина интервала Δ(z₁, …, z_j) равна (1/2ⁿ)^s.

При этом интервал Δ(0,0, …, 0) содержит левый конец единичного отрезка, а интервал Δ(2ⁿ — 1, …, 2ⁿ) — правый конец.

На рис. 6.1, рис. 6.2 и рис. 6.3. приведены соответственно первое, второе и третье разбиения единичного отрезка.

Рие. 6.З. Третье разбиение (m = 3) гиперкуба D_y(а) и отрезка [0.1] (б)

Будем считать, что точка у (v), соответствующая точке v, содержится в гиперкубе D(z₁, …, z_s), если v принадлежит интервалу Δ(z₁, …, z_s). Построенное таким образом отображение у (v) является однозначным и непрерывным.

Комментарии запрещены.