Процедура поиска точки глобального минимума х* аппроксимирующей модели может быть упрощена, если в качестве математической модели использовать кусочно-кубическую кривую S_N(х), проходящую через точки испытаний (x_i, Q(x_i)), i = 1, 2, …, N, и моделирующую поведение функции Q (х) на отдельных отрезках интервала |a, b| полиномами третьей степени Р₃(х) = ∑α_kⁱx^k. В этом случае поиск точки глобального минимума х* произвольной кривой Q (х) может быть осуществлен с помощью метода кусочно-кубической аппроксимации F¹⁵, в котором точки испытаний на каждом k-м шаге выбираются независимо от информации о поведении функции Q(x) и равномерно располагаются на интервале [a, b]:

x_i^(k) = a + i(b-a)/(N_k-1), i = 0, 1, …, N_k — 1.

Общее число точек испытаний N_k, по которым на k-м шаге строится математическая модель S_Nk (х), аппроксимирующая функцию Q (х), определяется по итерационной формуле:

N₁ = 5; N_k+1 = 2N_k — 1, k = 1, 2, 3,…

В новых точках, не совпадающих с уже проведенными испытаниями

x_i^(k+1) = (x_i^(k) + x_i-1^(k))/2,

проводятся дополнительные вычисления функции Q (х). На первом шаге (k = 1) используется информация обиспытаниях в пяти точках, на втором шаге (k = 2) — в девяти точках, среди которых в пяти уже проведены испытания, т. е. дополнительно вычисляется значение функции Q (х) только в четырех новых точках и т. д,

На k-м шаге поиска с помощью метода кубической интерполяции F⁽⁶⁾ строится совокупность аппроксимирующих полиномов P₃⁽ⁱ⁾(х), которые используются для описания функции Q (х) не в точках (x_i-1^(k), x_i^(k), x_i+1^(k), x_i+2^(k)), по которым каждый из них построен, а только на подынтервалах [x_i^(k), x_i+1^(k)], кроме концов интервала [a, b], где полиномы Р₃⁽¹⁾(х) и P₃^N_k-1(х) аппроксимируют функцию Q (х) на подынтервалах [а, х₂] и [x_Nk-3, b] соответственно. При этом на каждом шаге поиска значения коэффициентов совокупности полиномов Р₃⁽ⁱ⁾(х), образующих кусочно-кубическую кривую S_Nk(х), должны рассчитываться заново. Пример построения кусочно-кубической модели S_N2(х) на втором шаге поиска (к = 2) показан на рис. 4.4.

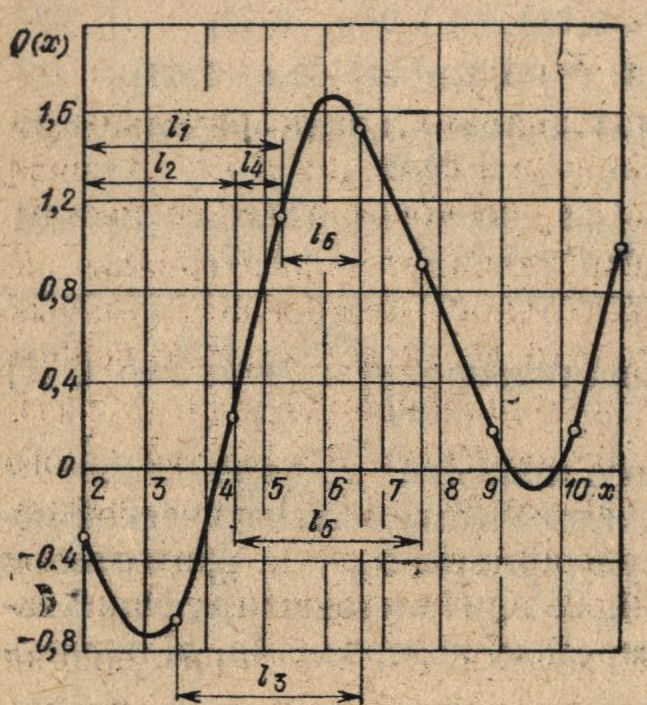
Рис. 4.4. Пример построения кусочно-кубической модели по девяти точкам в алгоритме F¹⁵

Здесь подынтервалы l₁, l₃, l₅ являются областями определения кубических парабол P₃⁽¹⁾(x), Р₃⁽²⁾(х), Р₃⁽³⁾(х), а подынтервалы l₂, l₄, l₆ — областями, где функция Q (х) = x/10+cos x аппроксимируется каждым из построенных полиномов третьей степени.

Построение кусочно-кубической модели считается законченным на k-м шаге, если относительная ошибка между значениями функции Q(x) и значениями, полученными по математической модели точках испытаний (k + 1)-го шага, меньше некоторого заданного значения ε:

max |[Q(x_i) — S_Nk(x_i)]/Q(x_i)| ≤ ε

При выполнении неравенства (4.34) в каждой точке x_i*∈[х_i^(k), х_i+1^(k)], являющейся точкой минимума полинома Р₃⁽ⁱ⁾ (х), которая определяется с помощью метода F⁶ делается дополнительное,испытание. В качестве приближенной точки глобального минимума выбирается точка х, обеспечивающая минимальное значение функции Q (х) по всем проведенным испытаниям N:

Q(x*) = min Q(x_i)

Таким образом, алгоритм F¹⁵ позволяет построить аппроксимирующую модель S_N(х) при помощи совокупности полиномов третьей степени. Однако для запоминания каждого полинома P₃⁽ⁱ⁾(х) требуется дополнительный объем памяти, который быстро растет с увеличением точности ε совпадения математической модели S_N (х) с минимизируемой функцией Q (х).

Этого недостатка лишен алгоритм F¹⁶ реализующий метод кусочно-линейной аппроксимации, в котором на каждом шаге поиска в качестве аппроксимирующей модели непрерывной функции Q (х) используется кусочно-ломаная кривая L_N (х) (полиномиальный сплайн первой степени). При этом точки текущих испытаний x_i, i = 1, 2, …, N_k-1, необходимые для построения математической модели L_N(х), выбираются таким же образом, как и в алгоритме F¹⁵. Основной характеристикой аппроксимирующей модели L_Nk(х) является число J_Nk подынтервалов [x_i-1, x_i+1], в которых обеспечивается выполнение неравенства:

L_Nk(x_i) ≤ L_Nk (х) для всех х∈[x_i-1, x_i+1].

Эти подынтервалы называются, подынтервалами, «подозрительными» на существование в них локального минимума функции Q (x). В связи с простотой аппроксимирующей модели L_Nk(х) поиск точек ее локальных минимумов, определяющих «подозрительные» подынтервалы, не
представляет труда. Процесс последовательного построения ломаны кривых L_Nk(х) заканчивается, кац только достигается качественное соответствие между структурой кусочно-линейной модели L_Nk(х), достроенной на k-м шаге поиска, и функцией Q (х). В качестве такого соответствия принимается значение параметра m (J_Nk), показывающего, сколько раз подряд число «подозрительных» подынтервалов J_Nk кусочно-линейной модели повторилось при ее уточнении. При повторении структуры кусочно-линейной модели L_Nk(х) m раз подряд (J_Nk = J_Nk+1, , …, J_Nk+m) считается, что функция Q (х) имеет такое же число и расположение локальных минимумов, как и ее кусочно-линейная модель, полученная на (k + m)-м шаге.

После построения кусочно-линейной модели L_Nk(х), адекватной минимизируемой функции Q(x), определение приближенного значения точки глобального минимума х сводится к минимизации одномерной унимодальной функции, являющейся частью кривой Q(x*) в каждом из «подозрительных» подынтервалов [x_i-1^(k), x_i+1^(k)], к = 1, J_Nk. При этом может быть использован любой из алгоритмов унимодального поиска. Таким образом, алгоритм F¹⁶ позволяет определить все локальные минимумы функции Q (х) и выбрать среди них тот, который обеспечивает наименьшее значение функции Q (х).

В качестве примера на рис. 4.5 показаны две кусочно-линейные модели функции Q (х) = x/10 + cos х (сплошная лривая), полученные при поиске минимума с помощью алгоритма F¹⁶. Кусочно-линейная модель L₅ (х), полученная на первом шаге, обозначена пунктирной кривой, а модель L₉ (х), полученная на втором шаге,— штрихпунктирной кривой. Точками отмечены испытания, проведенные на первом шаге, а крестиками — на втором. При значении m = 2 построение кусочно-линейной модели заканчивается выделением двух (J_N = 2) «подозрительных» подынтервалов (заштрихованные участки оси х), в которых в дальнейшем осуществляется поиск локального минимума с помощью одного из методов (F¹ — F¹⁰) минимизации унимодальных функций.

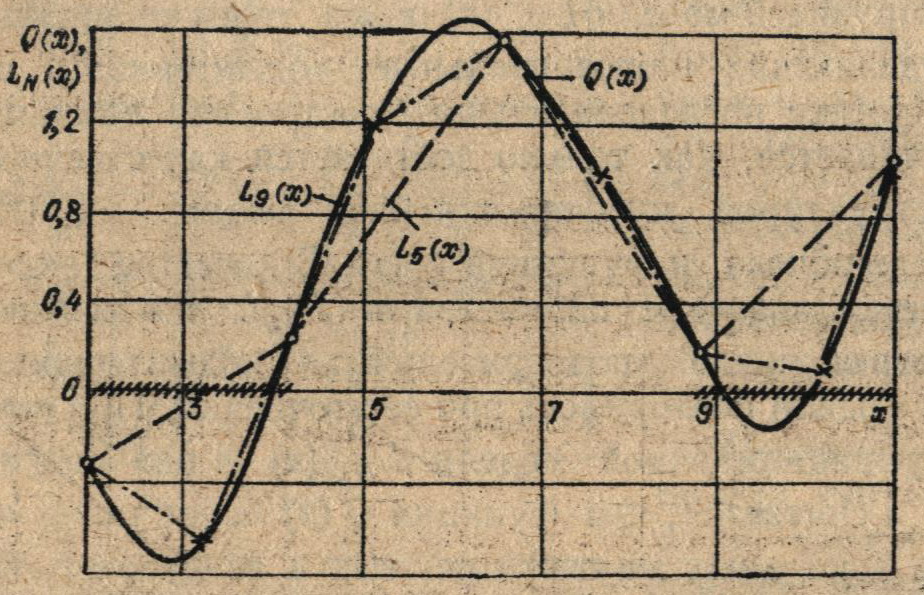
Рис. 4.5. Стратегия поиска глобального минимума по методу кусочно-линейной аппроксимации

Комментарии запрещены.