Пусть после проведения k испытаний имеет место ситуация III (рис. 3.7, в, см. предыдущий пост):

a_k < x_k < b_k; Q(a_k) > Q (x_k) < Q (b_k),

которая в силу унимодальности функции Q (х) гарантирует, что точка минимума x:* будет находиться внутри интервала [а_k, b_k]

a_k < x* < b_k.

В дальнейшем совокупность точек (a_k, x_k, b_k), приводящую к ситуации III, будем называть совокупностью «удачных точек».

Рассмотрим класс методов, называемых методами полиномиальной интерполяции, основная идея которых заключается в том, что по информации о m испытаниях (x_i, Q (x_i)) i = 1, 2, …, m строится интерполирующий полином φ_n(х) степени n ≤ m — 1, обладающий следующими свойствами:

φ_n(х) является равномерным приближением минимизируемой функции на интервале [а_k, b_k]:
точка минимума х* полинома φ_n(х) определяется достаточно просто.

Отмеченные свойства полинома φ_n(х) позволяют на каждом шаге поиска использовать для сокращения текущего интервала неопределенности не только информацию о точках испытаний x_i, но и информацию о значениях функции Q (x_i) в этих точках.

Для трех точек испытаний (m = 3) в качестве полинома φ_n(х) в методе квадратичной интерполяции F⁵ используется интерполяционный многочлен Лагранжа:

φ₂(x) = α₀ — α₁х + α₂х² = Q (a_k)((x — x_k) (x — b_k))/((a_k — x_k)(a_k — b_k)) + Q (x_k)((x — a_k) (x — b_k))/((x_k — a_k)(x_k — b_k)) + Q (b_k)((x — a_k) (x — x_k))/((b_k — a_k)(b_k — x_k))

который имеет минимум x_min во внутренней точке интервала [а_k, b_k] только тогда, когда α₂ > 0. т. е. тогда, когда для совокупности «удачных точек» выполняется неравенство:

Q (a_k)/(a_k — x_k)(а_k — b_k) + Q (x_k)/(x_k — a_k) (x_k — b_k) + Q (b_k)(b_k — x_k) (b_k — x_k) > 0.

В этом случае из условия dφ₂/dx = 0 нетрудно получить, что

x* = -α₁/2α₂.

После проведения испытания в точке х осуществляется сокращение интервала неопределенности, содержащего точку минимума х*, и определяется новая совокупность «удачных точек». При этом возможны следующие четыре случая.

Случай 1: х* < х_k; Q(х*) < Q (х_k) (рис. 3.8, а), х*∈[а_k, х_k];[x_k, b_k] — из рассмотрения исключается; a_k+i = а_k; b_k+i = х_k; х_k+1 = х*.

Случай 2: х* < x_k; Q (х*) ≥ Q (х_k) (рис. 3.8, б) х* ∈ [х, b_k]; [а_k, х] — из рассмотрения исключается; a_k+1 = х; b_k+1 = b_k; x_k+1 = х_k.

Случай 3: х* > х_k; Q (x*) < Q (х_k) (рис. 3.8, б) x* ∈ [x_k, b_k]; [а_k, х_k] — из рассмотрения исключается; a_k+1 = х_k; b_k+1 = b_k; x_k+1 = х*.

Случай 4: x* > x_k; Q (x*) ≥ Q (x_k), (рис. 3.8, г)
x* ∈ [a_k, x*]; [x*; b_k] — рассмотрения исключается;
a_k+1 = a_k; b_k+1 = x*; x_k+1 = x_k.

Предположим, что точка x_k делит отрезок [a_k, b_k] на две равные части длиной δ_k (a_k = x_k — δ_k, b_k = x_k + δ_k). Тогда, приняв, что Δ₁ = Q (x_k) — Q (a_k) и Δ₂ = Q (x_k) — Q (b_k), для x получим

x* = x_k + δ_k+1,
где

δ_k+1 = δ_k (Δ₁ — Δ₂)/(Δ₁ + Δ₂)

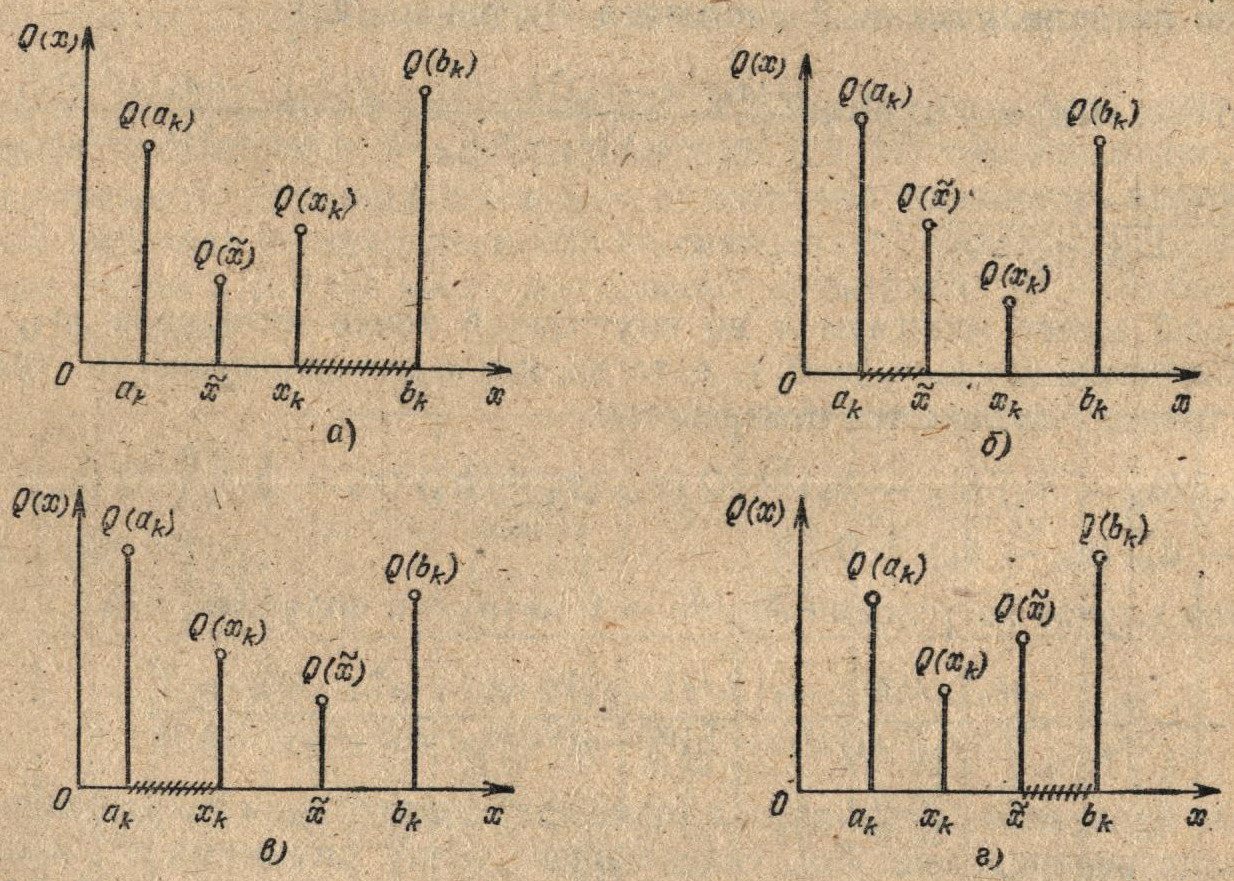
Рис. 3.8. Определение новой совокупности «удачных точек» в алгоритме F⁵

Нетрудно видеть, что для случаев 1 и 3 текущий интервал неопределенности [a_k+1, b_k+1] сокращается точно в два раза:

(b_k+1 — a_k+1)/(b_k — a_k) = 1/2,

а для случаев 2 и 4, о учетом условия (3.71), имеет место верхняя оценка:

(b_k+1 — a_k+1)/(b_k — a_k) ≤ 3/4.

Блок-схема метода F⁵, реализующего поиск минимума унимодальной функции Q (х), для которой задана исходная совокупность «удачных точек» (а, х₀, b), приведена на рис. 3.9.

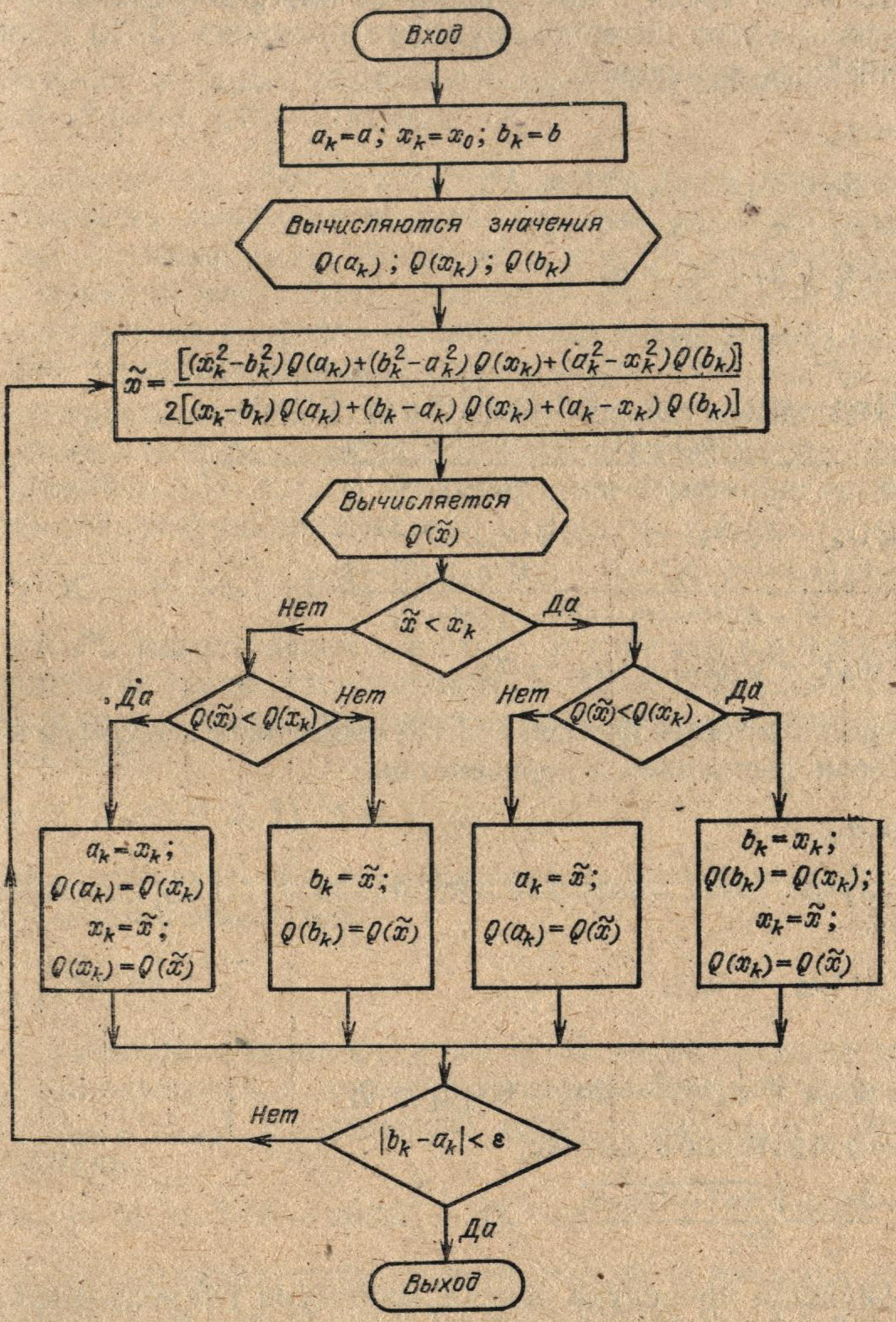
Рис. 3.9. Блок-схема алгоритма F⁵, реализующего метод квадратичной интерполяции

Для четырех точек испытаний (m = 4) поиск минимума унимодальной функции можно ввести с помощью метода кубической интерполяции F⁶, который отличается от метода F⁵ тем, что в нем в качестве интерполирующего полинома φ_n(х) используется кубическая парабола:

φ₃(x) = α₀ + α₁x + α₂x² + α₃x³.(3.72)

Не нарушая общности рассмотрения, предположим, что совокупность «удачных точек» на каждом шаге поиска приводится к единична му интервалу с помощью преобразования

ξ = (х — a_k)/(b_k — а_k);
а_k = 0; х_k = k; х_к = к, b_k = 1, где 0 < k < r < 1.

Тогда, взяв эти точки в качестве узлов интерполяции, для определения коэффициентов интерполирующего полинома (3.72) запишем систему линейных уравнений:

Q(a_k) = α₀,
Q(x_k) = α₀ — α₁k + α₂k² — α₃k³,
Q(x_r) = α₀ + α₁r + α₂r² + α₃r³,
Q(b_k) = α₀ + α₁ + α₂ + α₃.

Интерполирующая функция (3.72) имеет один максимум и один минимум, если выполняется неравенство:

α₂² ≥ α₁α₃, (3.73)

В этом случае точка минимума х* полинома φ₃(х) определяется по формуле

х* = a_k + (b_k — a_k)ξ*. (3.74)

Дальнейшая процедура поиска минимума унимодальной функции Q (х) по методу кубической интерполяции F* аналогична процедуре метода F⁵, так как связана с сокращением интервала неопределенности [a_k, b_k] и выбором новой совокупности «удачных точек» для (k + 1)-го шага из уже проведенных испытаний в точках (а_k, b_k, х_k, х_r, х*).

В связи с вышесказанным при поиске минимума унимодальной функции с высокой степенью точности ε необходимо последовательно применять сначала методы сокращения интервала неопределенности, до тех пор пока не будет получена совокупность «удачных точек», и затем методы полиномиальной интерполяции. Причем при минимизации функции, обладающей на интервале неопределенности большими по величине производными высших порядков, целесообразно использовать методы F¹ — F⁴, а в тех случаях, когда минимизируемая функция является гладкой функцией, близкой к квадратичной параболе,— методы F⁵ и F⁶.

Комментарии запрещены.