Асимптотической устойчивости по Ляпунову. Неустойчивости по Ляпунову
Определение (асимптотической устойчивости по Ляпунову): Невозмущенное движение x = 0 системы (1.19) называется асимптотически устойчивым по Ляпунову относительно величин x, если
а) оно устойчиво
б) если существуют такое число Δ > 0, что для любых начальных возмущениях x(t0), удовлетворяющих условию ||x0||<Δ, выполняется условие lim x (t, x0) = 0 при t→∞. (1.25)
Геометрическая интерпретация определения асимптотической устойчивости по Ляпунову в пространстве состояний x1,…,xN
На рис.1.8 представлена геометрическая интерпретация определения асимптотической устойчивости по Ляпунову. Начав в начальный момент времени t=t0 движение из точки М0, лежащей в Bδ — окрестности начала координат, изображающая точка М в случае асимптотической устойчивости нулевого положения равновесия (начала координат) при t ≥ t0 не выйдет из Bε-окрестности начала координат и при t→∞ неограниченно будет приближаться к началу координат.
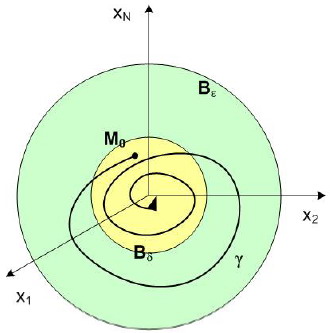
Рис.1.8 Геометрическая интерпретация определения
асимптотической устойчивости по Ляпунову
Определение (неустойчивости по Ляпунову): Невозмущенное движение x=0 системы (1.19) называется неустойчивым по Ляпунову относительно величин x=(x1,…,xN)T, если существуют число ε > 0 такое, что для любого числа δ > 0 существует решение x(t) уравнений (1.11) и момент времени t1 > t0 такие, что, хотя || x(t0) || < δ, тем не менее || x(t1) || > ε.
Геометрическая интерпретация определения неустойчивости по Ляпунову в пространстве состояний x1,…,xN
На Рис.1.9 представлена геометрическая интерпретация определения неустойчивости по Ляпунову. Начав в начальный момент времени t=t0 движение из точки М0, лежащей в Bδ-окрестности начала координат, изображающая точка М через конечный интервал
времени при t = t1 выйдет из Bε-окрестности начала координат.
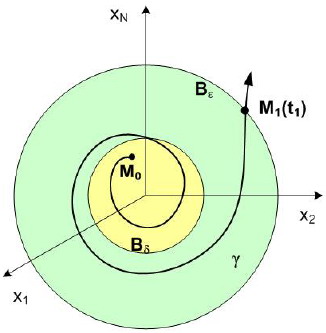
Рис.1.9 Геометрическая интерпретация определения неустойчивости по Ляпунову
Замечание: Устойчивость невозмущенного движения представляет собой структурное свойство системы в любой момент времени оставаться в малой ε-окрестности этого движения при малых начальных возмущениях, лежащих в δ-окрестности начального положения невозмущенного движения. Асимптотическая устойчивость невозмущенного движения означает, кроме того, что система с течением времени приближается к невозмущенному движению.