Чтобы вывести уравнения возмущенного движения введем новые переменные, представляющие собой отклонения (или вариации) x₁, x₁^•=x₂ возмущенного движения q(t), q^•(t) (1.5) от невозмущенного ξ(t), ξ^•(t) (1.3), а именно:
q(t) = ξ(t) + x₁, q^•(t) = ξ^•(t) + x₁^•. (1.15)

Подставим замену переменных (1.15) в уравнения движения (1.14). В результате получим уравнения движения для возмущений x₁:
A(ξ(t)+x₁)(ξ^•• + x₁^••) + b(ξ^•+x₁, ξ^•+x₁^•) + c(ξ+x₁) = Q_Н ξ+x₁,ξ^•+x₁^•) (1.16)

Определение. Дифференциальные уравнения движения (1.16), получающиеся из исходных уравнений (1.2) путем замены (1.15), называются уравнениями возмущенного движения.

Уравнения возмущенного движения (1.16) можно записать в форме Коши (1.17), если обозначить x₁^• = x₂, x₁(t₀) = x₁₀ x₂^• = f(x₁, x₂), x₂(t₀) = x₂₀. (1.17)

Здесь f(x₁, x₂) = A^-1[Q_Н(ξ+x₁,ξ^•+x₂) — A(ξ+x₁)ξ^•• — b(ξ^•+x₁, ξ^•+x₂) — c(ξ+x₁)].

Уравнения возмущенного движения в форме Коши (1.17) запишем для удобства дальнейшего изложения в виде

dx/dt = F(x), x (t₀) = x₀. (1.18)
Здесь x = (x₁^T, x₂^T)^T= (x₁,…, x_2n)^T — 2n-мерный вектор-столбец отклонений возмущенного движения от невозмущенного движения, F(x) = (x₂^T, f^T)^T — вектор-столбец правых частей уравнений движения. Будем считать, что правые части F(x) не зависят от времени. Система дифференциальных уравнений (1.18) имеет размерность N = 2n.

Заметим, что F(0) = 0, поскольку f(0, 0) = 0, поэтому уравнения (1.18) имеют нулевое решение x(t) = 0. (1.19)

Нулевое решение (1.19) описывает невозмущенное движение уравнений движения (1.18). Решение (1.19) соответствует невозмущенному движению ξ(t), ξ^•(t) (1.3) исходных уравнений (1.1).

Таким образом, переход к отклонениям x₁, x₂ (замена переменных) (1.15) позволяет свести задачу исследования устойчивости невозмущенного движения ξ(t), ξ^•(t) системы (1.1) к задаче исследования устойчивости нулевого положения равновесия x = 0 системы (1.18), записанной в форме Коши.

Замечание: Уравнения в форме Коши используются для описания поведения не только механических систем, но также электромеханических, биологических, химических, экономических и т.д. Геометрическая интерпретация уравнений возмущенного движения (1.18)

Уравнения возмущенного движения (1.18) описывают движение изображающей точки М с координатами x₁,…, x_N вдоль некоторой траектории γ (рис.1.6).

При этом скорость U = (U₁, U₂,…, U_N)^T движения изображающей точки М,
направленная по касательной к этой траектории, определяется правыми частями уравнений (1.18)
U₁ = F₁, U₂ = F₂, … , U_N = F_N. (1.20)

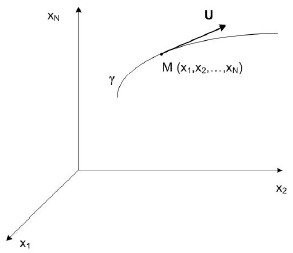
Рис.1.6 Геометрическая интерпретация уравнений возмущенного движения (1.18)

Замечание. При решении конкретных задач уравнения возмущенного движения необязательно приводить к форме Коши (1.18). Можно пользоваться уравнениями возмущенного движения (1.16) в форме Лагранжа II рода.

Сформулируем определения устойчивости в терминах вектора отклонений x=(x₁,…,x_N)^T для уравнений возмущенного движения (1.18) в форме Коши.
Наряду с невозмущенным движением x = 0 (1.19), удовлетворяющим нулевым начальным условиям, будем рассматривать возмущенные движения системы (1.18)
x = x (t), (1.21) удовлетворяющие начальным условиям
x(t₀) = x₀. (1.22)
Здесь величины x₀ — некоторые вещественные постоянные, представляющие начальные возмущения.

Определение (устойчивости по Ляпунову) Невозмущенное движение x=0 системы (1.19) называется устойчивым по Ляпунову относительно величин x=(x₁,…,x_N)^T, если для любого числа ε > 0, сколь бы мало оно не было, существует число δ(ε,t₀)>0 такое, что при начальных возмущениях x(t₀), удовлетворяющих условию
|| x₀|| < δ, (1.23) и при всех t ≥ t₀ будет выполняться неравенство || x(t) || < ε. (1.24) В противном случае невозмущенное движение называется неустойчивым. Здесь ||x(t)|| = √x_i²

Геометрическая интерпретация определения устойчивости по Ляпунову в пространстве состояний x₁,…,x_N.

На рис.1.7 представлена геометрическая интерпретация определения устойчивости по Ляпунову в пространстве x₁,…,x_N. Начав в начальный момент времени t=t₀ движение из точки М₀, лежащей в B_δ-окрестности начала координат, изображающая точка М в случае устойчивости нулевого положения равновесия (начала координат) при t ≥ t₀ не выйдет из B_ε-окрестности начала координат.

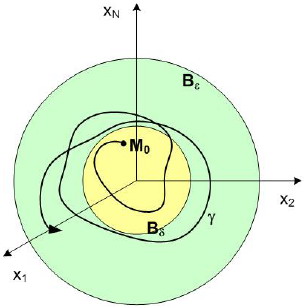
Рис.1.7 Геометрическая интерпретация определения устойчивости по Ляпунову

Комментарии запрещены.