Геометрические свойства знакоопределенной функции Ляпунова V(x)

1. Если функция V(x) знакоопределенная, то поверхность V(x₁, …, x_n)=c=const в пространстве (x₁, …, x_n) является замкнутой поверхностью (рис.3.1).

Если функция V(x) знакопостоянная или знакопеременная, то поверхность V = c =const разомкнутая.

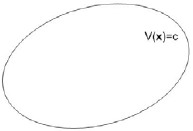
Рис.3.1 Поверхность V(x₁, …, x_n)=c=const для знакоопределенной функции V

2. Если функция V(x) знакоопределенная и |c₂| > |c₁|, то поверхность V = c₂ лежит снаружи поверхности V = c₁ и поверхности не имеют общих точек (рис.3.2).

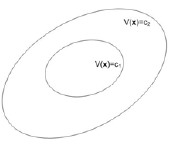
Рис.3.2 Взаимное расположение поверхностей V = c₁, V = c₂ при c₂ > c₁ для знакоопределенной функции V

3. Поскольку вектор grad V направлен по нормали к поверхности V(x)=c в сторону возрастания функции V (рис.3.3). Тогда для положительно-определенной функции V вектор grad V направлен во внешнюю часть замкнутой поверхности V = c, а для отрицательно-определенной функции V — во внутреннюю часть замкнутой поверхности V = c.

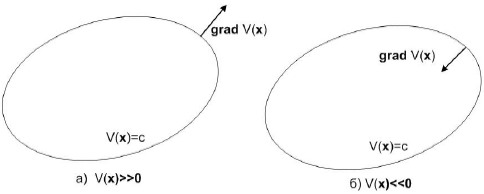
Рис.3.3 Взаимное расположение поверхностей V = c₁, V = c₂ при c₂ > c₁
для знакоопределенных функций V

4. Если функция V положительно-определенная, то при достаточно малых значениях c изображающая точка М с координатами (x₁, …, x_n) при перемещении в сторону возрастания функции V(x₁, …, x_n) пересекает поверхность V=c изнутри наружу (и наоборот). Если функция V отрицательно-определенная, то при достаточно малых значениях c изображающая точка М с координатами (x₁, …, x_n) при перемещении в сторону возрастания функции V(x₁, …, x_n) пересекает поверхность V=c снаружи внутрь.

Комментарии запрещены.