Общие представления об устойчивости движения

Основы теории устойчивости движения были разработаны великим русским ученым А.М.Ляпуновым (1857 — 1918).

Разработка любого технического устройства (манипулятора, мобильного робота, спутника, гироскопической системы и т.д.) является сложной научно-технической проблемой. Поскольку на практике реализуются лишь устойчивые движения, то важнейшей задачей, которая возникает уже на этапе проектирования любой машины или механизма, является задача обеспечения устойчивости их движений.

Эта задача заключается в определении условий, при которых заданное (назовем его программным) движение исследуемой системы будет устойчивым, а переходные процессы будут удовлетворять заданным свойствам.

В действительности (при реальном функционировании) система совершает незаданное (программное) движение, которое планировал инженер-разработчик, а некоторое другое (действительное) движение. Это действительное движение возникает в системе вследствие того, что в начальный момент времени имеются небольшие отклонения от
начального состояния программного движения и, возможно, существуют малые силы, которые не учитывались при моделировании системы.

Пример 1.1: Рассмотрим движение физического маятника массой m в однородном поле сил тяжести с ускорением g (рис.1.1), считая, что в оси его качания действуют силы вязкого трения. Маятник имеет потенциальную энергию П = mgl (1 — cos φ)
где l — расстояние от неподвижной точки до его центра масс, а φ — угол отклонения маятника от нижнего положения равновесия.

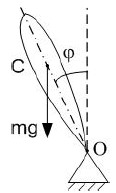
Рис.1.1.

Из уравнений движения можно вывести уравнение равновесия маятника ∂П/∂φ = 0 ⇔ mgl sin φ = 0, которое имеет два частных решения:
а) φ₁₀ = 0, описывающее нижнее положение равновесия;
б) φ₂₀=пи, — верхнее положение равновесия.

Верхнее положение равновесия, хотя оно и существует, в действительности не наблюдается, поскольку всегда существуют малые начальные отклонения, вследствие чего система «уходит» от этого равновесия. Нижнее положение равновесия наблюдается в действительности, поскольку при малых начальных отклонениях маятник возвращается к этому положению равновесия.

Поскольку практически невозможно удовлетворить начальным условиям программного движения, то возникает вопрос:
Каким образом будет вести себя система в дальнейшем?

Интуитивно ясно, что, если при действительном движении система с течением времени будет все больше отклоняться от заданного программного движения, то это программное движение будет невозможно реализовать на практике, поскольку оно является 2 неустойчивым. Если же система с течением времени мало отклоняется от заданной программы, то эту программу можно считать устойчивой.

Сформулируем данные выше интуитивные представления об устойчивости на математическом языке.

Комментарии запрещены.