Особенности определения устойчивости по Ляпунову
Особенности определения устойчивости по Ляпунову
1. В основе определения устойчивости по Ляпунову лежит понятие числа, а не бесконечно малой величины.
Замечание. Это факт имеет большое практическое значение, поскольку по заданным величинам ε1, ε2, характеризующим отклонения возмущенного движения от невозмущенного в любой момент времени, можно найти другие числа δ1, δ2, характеризующие численные значения начальных возмущений, которые являются численно малыми, но конечными.
Пример: Найдем числа δ1, δ2 по заданным числам ε1, ε2 для физического маятника в случае отсутствия трения в оси качания. Уравнение малых колебаний маятника около нижнего положения равновесия имеет вид
x •• + ω02 x = 0, (1.10)
где x — отклонение маятника от нижнего положения равновесия, ω02 = mgl/JО, ω0 — собственная частота маятника, JО — момент инерции маятника относительно оси качания.
Решение уравнений (1.10) представляет собой гармонические колебания
x = A cos(ω0t +β), x • = v = -Aω0 sin(ω0t +β). (1.11)
Маятник находится в окрестности нижнего положения равновесия все время при любых малых
начальных условиях x0, x0•, которые определяют постоянные A и β, поэтому нижнее положение маятника является устойчивым.
На фазовой плоскости собственные колебания описываются эллипсами с полуосями a = A и b=Aω0
x2 + v2/ω2 = A2. (1.12)
Если мы возьмем произвольные достаточно малые числа ε1, ε2 > 0 и найдем по ним числа δ1, δ2 > 0 (δ1 = δ2 = δ > 0) такие, что все решения x(t), x•(t) уравнения (1.10), начальные условия которых
x(t0), x•(t0) удовлетворяют неравенствам (1.7), будут оставаться в малой окрестности движения (1.11) в соответствии с (1.8), то движение (1.11) будет устойчивым по Ляпунову относительно переменных x, x•. Для того, чтобы найти числа δ1, δ2 возьмем на фазовой плоскости ε-круг радиуса ε (рис. 1.5)
Bε: x2 + v2 = ε2 (1.13) и рассмотрим эллипс (1.12), целиком лежащий в этом круге.
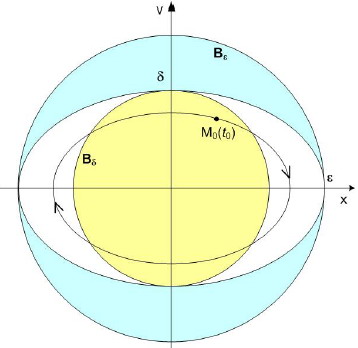
Рис. 1.5 Нахождение числа δ по заданному числу ε
Далее выберем второй δ-круг Bδ радиуса δ = min (a, b), целиком лежащий внутри данного эллипса (1.12). Поскольку все траектории данной системы представляют собой эллипсы (1.12) с различными значениями величины A, то ясно, что все траектории системы (1.10), стартующие из этого δ-круга (из точки M0(t0), не выйдут из ε-круга (1.13) при всех t ≥ t0. В результате имеем:
для любых значений ε1 = ε2 = ε числа δ1 = δ2 = δ, где δ < εω0, если ω0 < 1, и δ < ε/ω0, если ω0 > 1.
2. Возмущения действуют только в начальный момент времени (мгновенные возмущения).
3. Возмущенное движение происходит при тех же силах, что и невозмущенное движение. Силы не возмущаются.
4. Устойчивость рассматривается на бесконечном интервале времени t0 ≤ t < ∞. 5. Устойчивость по Ляпунову - понятие математическое в том смысле, что в определении говорится об устойчивости относительно величин q, q•. Невозмущенное движение может быть устойчиво относительно одних величин и неустойчиво относительно других.
Пример. Движение точки по круговой орбите с постоянной угловой скоростью в центральном ньютоновском поле сил устойчиво относительно радиус-вектора точки и ее тангенциальной скорости, но неустойчиво относительно декартовых координат точки.