Экспериментальный подход к получению модели объекта
Мы познакомились с общими вопросами моделирования, ввели понятие «имитационное моделирование» и необходимость для его реализации имитационной системы. Современные имитационные системы представляют собой мощные средства для изучения систем. Однако вычислительная техника со всеми её огромными возможностями не может решать задачи получения исходных моделей. И сегодня, и в будущем построение моделей окружающего мира будет совершаться напряженной творческой деятельностью. Никакие затраты машинного времени не заменят их — ЭВМ только облегчит этот процесс, помогая в решении рутинных задач.
До сих пор при рассмотрении вопросов моделирования мы считали, что исходная модель известна, и наша задача воспроизвести её на ЭВМ. Специалисты в области моделирования на ЭВМ начинают с формулировки проблемы машинного моделирования, располагая моделями в той или иной форме, т.е. они не рассматривают вопросы получения исходных моделей реального объекта. Данная глава посвящена решению этой важной задачи.
Можно выделить два основных подхода к решению задачи получения исходной модели:
• теоретический (аналитический);
• экспериментальный.
Теоретический подход к получению модели основан на применении фундаментальных законов природы и в его основе лежат математические методы.
Для сложных многосвязных, нелинейных, стохастических объектов реального мира при формировании модели, как правило, вводят те или иные упрощения.
Аналитический подход наиболее оправдан при разработке новых, несуществующих объектов, когда проектируется новая система. Но когда речь идет о системах автоматического управления, АСУ ТП, то, как правило, их разрабатывают применительно к физически существующим объектам. Объект рассматривается как заданная часть, для которой и разрабатывается система управления.
В этом случае широко используется экспериментальный подход.
Преимущества экспериментального получения модели объекта заключается в том, что при эксперименте с реальным объектом несущественные факторы, переменные, связи не проявляются или их влияние незначительно. В связи с этим аналитическое представление результатов эксперимента существенно упрощается. Конечно, получаемая модель должна быть адекватна изучаемому реальному объекту.
Полученная тем или иным подходом модель и будет исходной, первоначальной для реализации имитационной модели.
Математические модели широко используются в составе систем управления. На их основе современная теория управления решает задачи оптимизации, адаптации, строит двухшкальные системы и т.п. В этих случаях модели в системах управления выполняют роль датчика состояния и поведения системы.
Получение математической модели по экспериментальным данным называется идентификацией.
В общей постановке задача идентификации формулируется следующим образом:
по реализации входных и выходных сигналов определить оператор А, устанавливающий математическую связь между входами и выходами объекта z(r)=Au(t) (рисунок ниже), где u(t) — вектор управляющих воздействий; z(t) — вектор выходов; v(t) — вектор возмущающих воздействий.
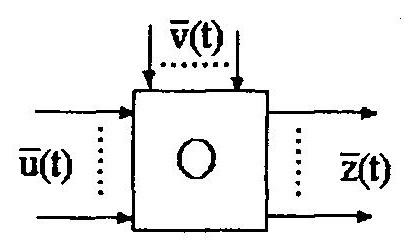
В теории идентификации определяется оптимальная оценка оператора А по результатам обработки экспериментальных данных.
В общем случае оператор А отражает структуру и параметры объекта идентификации. Наличие априорных данных может существенно ускорить процесс получения решения. Если априорных данных мало или их вовсе нет, то решение задачи идентификации связано как с определением структуры оператора А (а значит и исследуемого объекта), так и с оценкой параметров этой структуры. В этом случае говорят об идентификации в широком смысле. Если же структура заранее известна или задача идентификации решается для заданной, выбранной структуры, то речь идет о параметрической идентификации или идентификации в узком смысле.
На практике часто можно идентифицировать каждый канал связи объекта в отдельности, независимо. Тогда схема идентификации одного канала принимает вид, представленный на рисунок ниже, где n(t) — аддитивная случайная помеха или шум наблюдения, искажающий выход z(t); y(f) — наблюдаемый выход объекта.
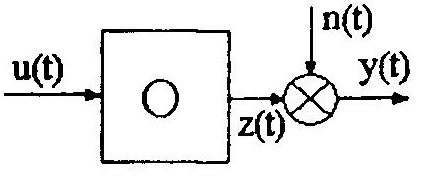
В этом случае имеем дело со скалярными величинами
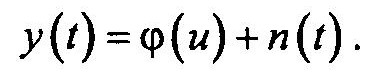
Решение этой задачи может быть осуществлено при подаче на вход объекта специального (тестового) сигнала — в этом случае говорят об активном способе идентификации. Если же такие специальные сигналы не могут быть поданы на вход, а в качестве входного сигнала рассматривается сигнал, воздействующий на объект в нормальном режиме функционирования, то тогда говорят о пассивном методе идентификации.
При детерминированной постановке задачи идентификации эксперименты реализуются при подаче на вход объекта ступенчатого сигнала, короткого импульса (близкого к δ-функции) и гармонического сигнала. В этих случаях оцениваются такие характеристики как переходная функция h(t), весовая функция w(t) и частотная характеристики.
В общем случае детерминированной задачи для произвольного входного сигнала u(t) на основе интеграла свертки имеем
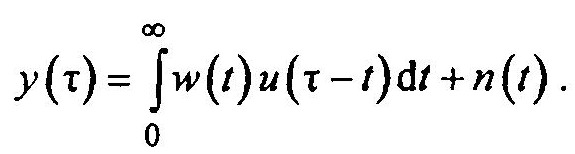
Здесь искомой является весовая функция w(t). Если помехи,
внешние возмущения существенны, то они могут так исказить истинный выход (правая часть уравнения представляет собой смесь истинного выхода и помехи), что решение относительно получить
трудно.
Следовательно, в общем случае при стохастическом характере изучаемого процесса, объекта не обойтись без статистического подхода.
На сегодняшний день разработано большое количество методов идентификации. Это методы идентификации линейных и нелинейных объектов, в частотной и во временной областях, идентификация при случайных воздействиях, беспоисковые и поисковые алгоритмы идентификации и т.п.
Представителями статистических методов идентификации являются методы, основанные на корреляционном и регрессионном анализах.