Рассмотрим класс алгоритмов, которые позволяют решение задачи нелинейного программирования свести к решению последовательности задач безусловной оптимизации.

В общем виде такое преобразование осуществляется при помощи специальным образом сконструированной функции, называемой штрафной функцией (функцией нагружения и т. д.):

Ф(х, c_r) = Q(x) + R(х, c_r) = Q (X) + с_rψ(х). (7.77)

где c_r > 0 — параметр штрафа; ψ(х) — индикаторная функция, R (х, c_r) = с_rψ(х) — штраф.

Если x∈D, то осуществляется минимизация функции Q (х). При нарушении ограничений (х не принадлежит D) функция Q (х) «штрафуется» на величину R(х, c_r), что и определяет название данного класса алгоритмов — методы штрафных функций. На рис. 7.4 показаны одномерная задача min(αх+β) (рис. 7.4, а) и эквивалентная ей задача минимизации функции штрафа Ф (х, с_r) при A_∞ = ∞ (рис. 7.4, б).

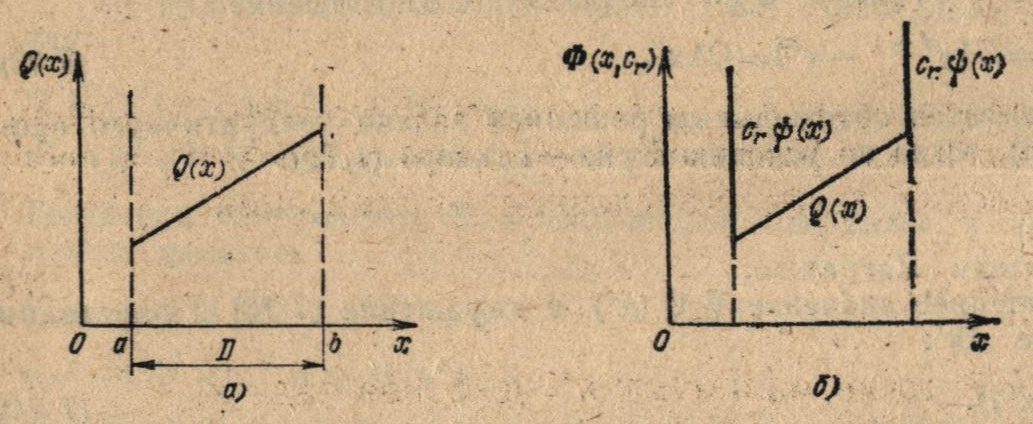
Рис. 7.4. Пример штрафной функции с бесконечно большим штрафом A_∞ = ∞

Штрафная функция, определяемая выражением (7.77), для больших значений A_∞ оказывается плохо обусловленной, т. е. вблизи оптимального решения х* ее гессиан имеет ряд собственных значений, стремящихся к бесконечности о ростом A_∞. Это приводит к тому, что структура минимизируемой функции Ф(х, с_r) приобретает овражный характер. Следует отметить, что чем меньше значение A_∞, тем менее ярко выражен овраг. Но, с другой стороны, с уменьшением A_∞ снижается точность определения оптимального решения х* исходной задачи (7.1). В связи G этим при преобразовании задачи нелинейного программирования к последовательности задач безусловной оптимизации целесообразно рассматривать не постоянное значение штрафа R(х, с_r), а менять его постепенно, увеличивая при приближении к точке минимума X* влияние ограничений на минимизируемую штрафную функцию Ф (х, c_r). Это требование накладывает на индикаторную функцию ψ(х) следующие ограничения. Она должна обладать следующими свойствами:

lim {c_rψ(x^r)}=0;
lim {Ф(х_r*, c_r)- Q(x*)}=0,

т. е. влияние штрафа R(х, с_r), удовлетворяющего этим условиям штрафной функции Ф(х, c_r), должно постепенно ослабевать, а последовательность решений задач безусловной минимизации:

Ф(х_r*, с_r) =min Ф(х, c_r) (7.78)

должна сходиться к точке минимума х* исходной задачи.

Конкретный вид штрафа R (х, с_r) нетрудно получить из условий оптимальности решения х* задачи выпуклого программирования (условий Куна—Таккера (1.76)—(1.79)).

Представим множители Лагранжа Ui в виде функции от параметра
λ_i ≥ 0:

u_i = λ_i², i = 1, 2, …, m. (7,79)

Очевидно, что условие u_ig_i(х) = 0 эквивалентно условию:

λ_ig_i(x) = 0, i = 1, 2, …, m. (7.80)

Предположим, что условия (7.80) не выполняются и их левая часть равна некоторой положительной величине а_r. Тогда можем записать:

λ_ig_i(х) = a_r, i = 1, 2, …, m.

Откуда получаем, что λ_i = a_r/g_i(х)

или, учитывая (7.79), для множителей Лагранжа получаем:
u_i = a_r²/g_i²(х), i = 1, 2, …, m..

Подставляя полученные значения u_i в последнее из условий Куна— Таккера, можем записать:

∇Q(x) — ∑a_r²∇g_i(x)/g_i²(x) = 0. (7.81)

Выражение (7.81) соответствует условию существования минимума (первые производные равны нулю) многопараметрической функции
без ограничений следующего вида:

Ф(х, c_r) = Q(x) + c_r∑(1/g_i(x)). (7.82)

Здесь c_r = а_r²— параметр штрафа, который выбирается таким образом, чтобы c_r → 0 при r → ∞ для обеспечения условий (7.80) в точке x* (точка x* является оптимальным решением исходной задачи);
ψ(х) = ∑(1/g_i(x)) — функция, которая при приближении к границе допустимой области D препятствует нарушению ограничений g_i(х), стремясь к бесконечности.

Таким образом, если начальное приближение х° является внутренней точкой, т. е. такой, в которой, все ограничения g_i(х) выполняются как строгие неравенства:

g_i (х°) > 0, i = 1, 2, …, m,

то оптимальное решение x_r* задачи безусловной минимизации штрафной функции (7.82) будет всегда находиться внутри допустимой области, так как функция R (х, c_r) ставит «барьер» против выхода из области D. Это свойство позволяет выделить в методах штрафов класс алгоритмов, реализующих методы внутренней точки (методы барьерных функций). При уменьшении параметра штрафа c_r уменьшается влияние штрафа R(х, c_r) и возрастает влияние критерия Q(х) на значение штрафной функции Ф(х, c_r). В связи с этим при с_r → 0 уменьшение Ф (х, с_r) возможно только за счет минимизации функции Q(х) без нарушения ограничений g_i(х). При r → ∞ точки минимума x_r* гиперповерхностей Ф(х, с_r) все более плотно подходят к точке минимума x* гиперповерхности соответствующей функции Q (х) = Ф (х, 0).

На pис. 7.5 в качестве иллюстрации приведены линии уровня семейства (пунктирные кривые) параметрических функций
Ф(x, c_r) = x + c_r(1/х + 1/(1 — x)),
построенные при различных значениях параметра с, для задачи одномерного поиска min {х}.

Рис. 7.5. Линии уровня штрафной функции Ф(х, c_r) для различных значений c₁ > c₂ > c₃

Другой тип функции штрафа можно получить, если предположить, что первое соотношение условий Куна—Таккера не выполняется:

ug_i (х) = c_r, i = 1, 2, …, m.

Тогда множители Лагранжа при условии, что g_i(х)≠0 имеют вид:

u_i = c_r/g_i(х).

Подставляя полученные значения u_i в последнее соотношение условий Куна—Таккера, получаем

∇Q(x) — ∑c_r∇g_i(x)/g_i(x) = 0. (7.83)

Выражение (7.83) соответствует условию существования минимума многопараметрической функции без ограничений следующего вида

Ф(х, c_r) = Q(x) + c_r∑ln(1/g_i(x)) = Q(x) — c_r∑ln(g_i(x)). (7.84)

Полученное выражение называется логарифмической функцией штрафа и обладает теми же свойствами, что и штрафная функция (7.82).

В том случае, когда допустимая область D является замкнутым выпуклым множеством, имеющим подмножество внутренних точек

D₀ = {x|g_i(x) > 0, i = 1, 2, …, m}. (7.85)

а функции Q (х) и g_i(х), i = 1, 2, …, m, являются непрерывными функциями, существует такая точка х∈D₀, что

lim Ф(х_r*, с_r) = Ф(х); (7.86)
lim Ф(х_r*, c_r) = Q(x) = min Q(x) (7.87)

при условии, что

R(x_r+1*, c_r+1) < R(x_r*, c_r). (7.88)

В том случае, когда начальное приближение х°, принадлежащее множеству внутренних точек D₀, априори задать трудно, для его определения можно применить следующую процедуру.

Предположим, что в произвольной точке х’ ограничения типа неравенств (а метод внутренних точек применим только для задач нелинейного программирования) удовлетворяются не для всех индексов j:

g_j(х’) ≤ 0, j ∈ J;
g_i(x’) > 0, i ∈ J, где J∪I = {1. 2, …, m}.

Тогда стратегия поиска точки х° ∈D₀ заключается в построении последовательности точек {x_k} таких, чтобы сумма нарушившихся ограничений уменьшалась по абсолютной величине, но при этом ни одно из уже выполненных ограничений не нарушалось:

max ∑g_j(x) = min{-∑ g_j(x)} (7.89)

при условии, что

g_i(x’) > 0, i ∈ J.

Для задачи (7.89) начальное приближение известно (это точка х’), поэтому применим для ее решения метод внутренних штрафов, который сводится к решению последовательности задач безусловной минимизации вида:

min (-∑g_j(x) + c_r∑(1/g_j(x))}. (7.90)

В процессе решения задачи безусловной оптимизации (7.90) появляются новые точки, в которых удовлетворяются одно или более ограничений из тех, что прежде не удовлетворялись, т.е. индексы из множества J переходят в множество I. При этом изменяется и сама вспомогательная задача (7.89). Точка х° считается определенной, когда множество индексов J становится пустым. Если в точке оптимального решения вспомогательной задачи (7.89) множество индексов J не пусто, то это означает, что ограничения исходной задачи нелинейного программирования (7.1) несовместны.

Эффективность метода внутренних точек в значительной степени зависит от выбранного начального значения параметра штрафа с₀. Если c₀ велико, то процесс поиска оптимального решения х* исходной задачи нелинейного программирования начинается далеко от границы допустимой области D, при малых значениях c₀, наоборот, процесс поиска начинается далеко от оптимального решения х*. В обоих случаях приходится тратить дополнительные усилия на решение последовательных задач безусловной оптимизации. В связи с этим выбор начального значения параметра штрафа c₀ можно осуществлять таким образом, чтобы модуль градиента штрафной функции в точке начального приближения имел минимальное значение:

∇Ф(x°,c₀) = min|∇Ф(x°, с)|.

Комментарии запрещены.