Программный комплекс для исследования линейных динамических систем
В данной статье представлены программные комплексы для моделирования непрерывных и непрерывно-дискретных динамических систем, разработанные сотрудниками института автоматики и вычислительной техники МЭИ.
Программный комплекс (ПК) МАСЛИН (машинный анализ и синтез линейных систем) предназначен для исследования линейных непрерывных стационарных систем с одним входом и одним выходом, задаваемых структурной схемой, в общем случае многоконтурной, с известными передаточными функциями ее звеньев, а также для решения задач параметрической оптимизации.
Программный комплекс МАСЛИН позволяет осуществлять:
1) графический ввод и редактирование структурной схемы, представленной в символах входного языка ПК, содержащего всего четыре элемента;
2) ввод и редактирование численных значений коэффициентов передаточных функций звеньев, составляющих структурную схему;
3) автоматическое преобразование структурной схемы для получения эквивалентной передаточной функции;
4) расчет и построение различных частотных характеристик;’
5) расчет переходных процессов исследуемой модели;
6) построение корневого годографа;
7) построение областей устойчивости в пространстве изменения двух любых параметров исследуемой системы;
8) решение задач параметрической оптимизации по желаемым частотной и временной характеристикам;
9) организацию библиотек моделей и макроблоков;
10) получение твердой копии на принтере как введенной структурной схемы, так и любой из рассчитанных характеристик.
Язык программирования — Turbo Pascal. Программный комплекс МАСЛИН ориентирован на персональный компьютер. Объём ПК на жестком носителе — 160 Кбайт.
При работе с программный комплексом МАСЛИН фаза редактор модели должна быть обязательно первой, так как все остальные фазы становятся доступными после входа в фазу редактор модели. Программный комплекс имеет очень простой входной язык моделирования. Проблемно-ориентированный язык (ПОЯ) для ввода модели исследуемой системы содержит всего четыре элемента:
1) линейное звено общего вида, задаваемое отношением полиномов числителя и знаменателя;
2) инвертор — линейное звено с передаточной функцией, равной 1;
3) соединительная линия;
4) макроблок (в программном комплексе КАЛИСТО отлаженную
модель системы или ее части можно объявить макроблоком и использовать в дальнейшем как еще одно линейное звено — макроблок).
Наборное поле для ввода модели представляет собой совокупность узлов (10×10), между которыми вводятся соответствующие блоки. Модель легко корректируется удалением или заменой того или иного элемента.
Ввод параметров элементов исследуемой модели осуществляется заданием числовых коэффициентов числителя и знаменателя в окне «ПАРАМЕТРЫ». После выбора входа и выхода исследуемой модели ПК преобразует исходную модель в эквивалентную передаточную функцию. Теперь исследователь может решать одну из задач, реализуемых в программном комплексе МАСЛИН.
Программный комплекс МАСЛИН по своей организации представляет собой пакет прикладных программ несложной структуры. На рисунке ниже приведен функциональный состав пакета.
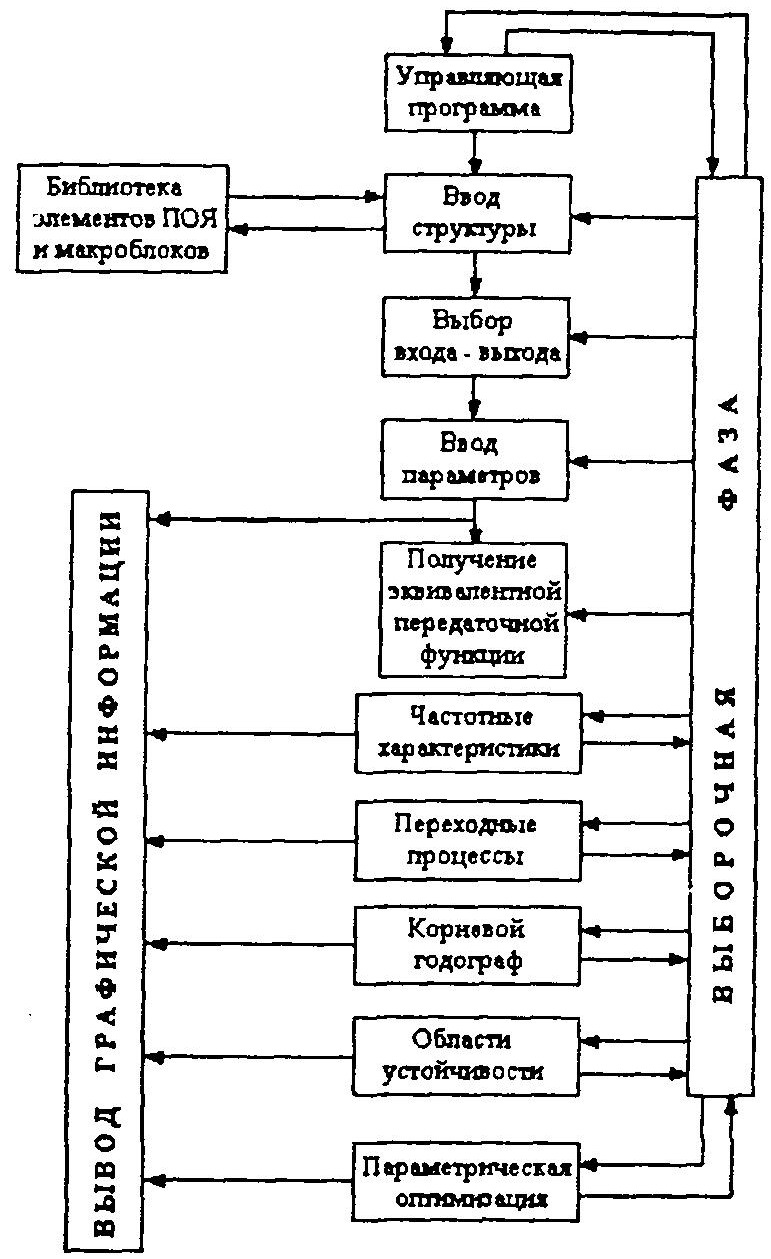
Кратко представим основные алгоритмы функционирования программного комплекса МАСЛИН.
В основе получения эквивалентной передаточной функции исследуемой системы лежат правила преобразования структурных схем. Эти правила основаны на том, что после преобразования исходная и эквивалентная структуры должны одинаково преобразовать поступающий на вход сигнал.
Правила преобразования структурных схем представлены на рисунке ниже.
Зная эти правила, легко преобразовать любую многоконтурную модель линейной системы с перекрещивающимися связями к эквивалентной передаточной функции. Эти правила преобразования заложены в пакет МАСЛИН.
Последовательное соединение:
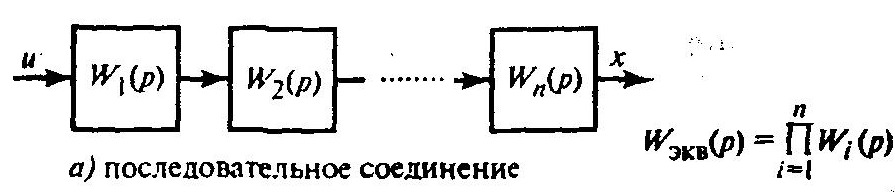
Параллельное соединение:
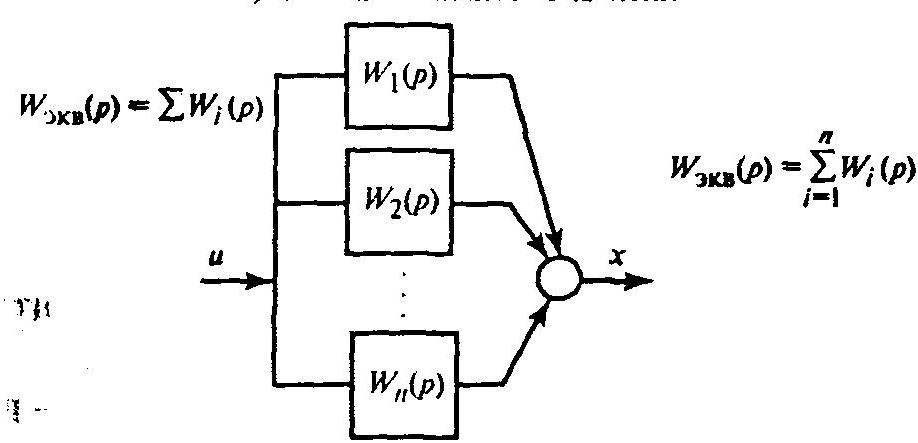
Соединение обратной связью:
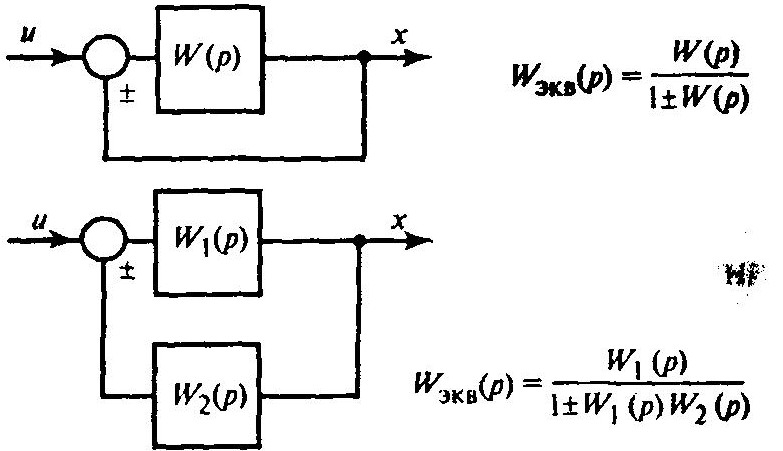
Перенос звена через узел и обратно:
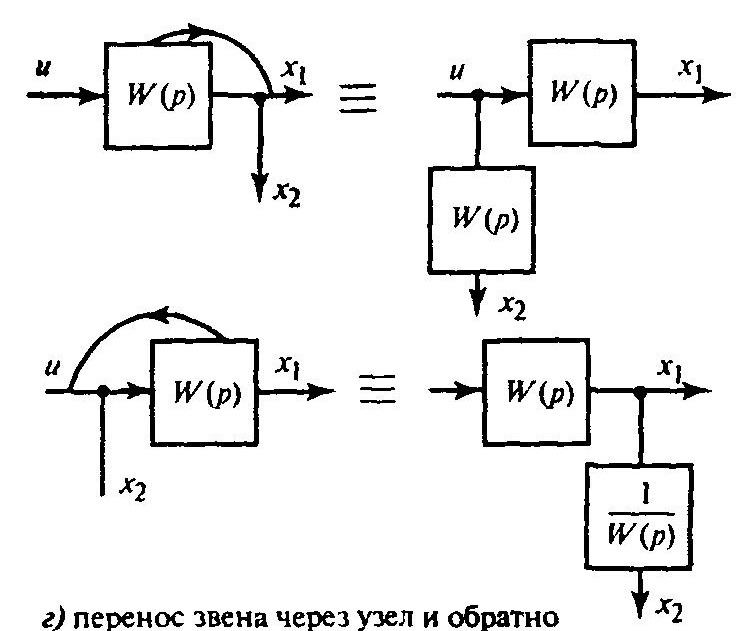
Перенос звена через сумматор и обратно:
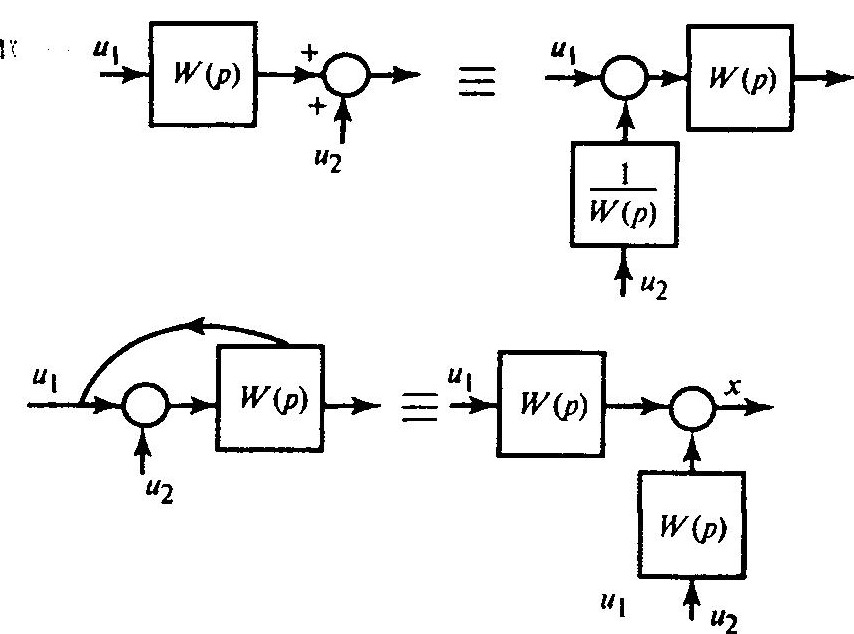
Сумматоры можно менять местами
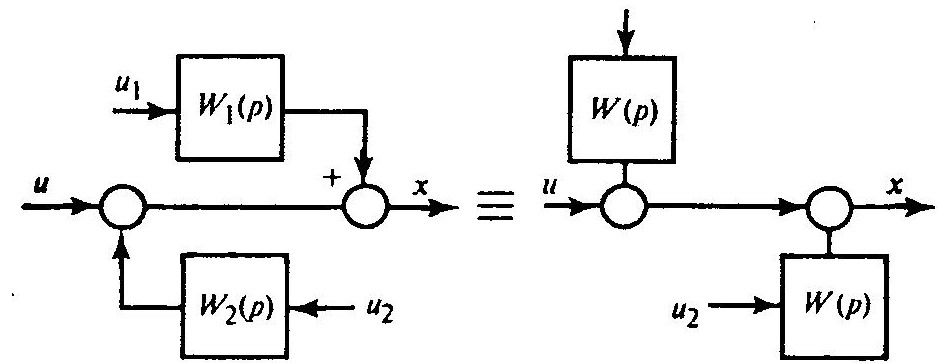
По эквивалентной передаточной функции строятся разнообразные частотные характеристики. Переходной процесс вычисляется по вещественно-частотной характеристике исследуемой системы по формуле
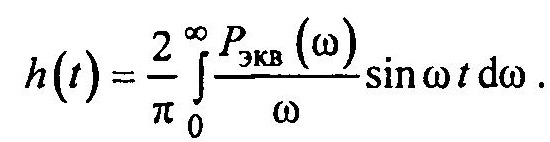
Управление работой в фазе расчета частотных характеристик осуществляется с помощью меню. Эта фаза содержит следующие шаги по построению частотных характеристик:
• выбор вида частотной характеристики;
• задание диапазона изменения частоты посредством указания начальной и конечной частот;
• расчет выбранной частотной характеристики и графический вывод на экран.
Для анализа линейных динамических систем интерес представляет поведение корней характеристических уравнений в зависимости от того или иного параметра исследуемой системы, что наглядно можно представить построением корневого годографа. Таким образом, корневой годограф представляет собой след корней на комплексной плоскости при варьировании того, или иного параметра.
Корневой годограф строится по характеристическому уравнению соответствующей системы — разомкнутой или замкнутой. Конечно, наибольший интерес представляет корневой годограф замкнутой системы.
Если передаточная функция разомкнутой системы
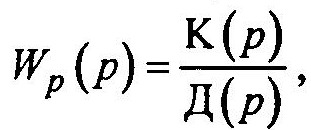
то характеристическое уравнение соответствующей
замкнутой системы примет вид
А(р) = К(р) + Д(р) = 0. (1)
Если выбрать варьируемый параметр (обычно это или коэффициент усиления или постоянная времени), то уравнение (1) посредством простейших преобразований приводится к виду
A(p) = P(p) + vQ(p) = 0,
где v — варьируемый параметр; Р(р) — часть, не зависящая от варьируемого параметра; Q(p) — часть, связанная с варьируемым параметром.
Если n — степень характеристического уравнения, то коневой годограф содержит след n-корней при 0 < v < бесконечность. Обозначим корни Р(р) = 0 через pi, i = 1,…,n; Q(p) = 0 через qj = 1,…,r, где r
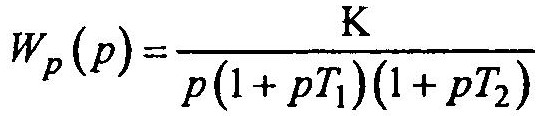
при варьировании коэффициента усиления v = k корневой годограф имеет вид (при Т1 > T2).
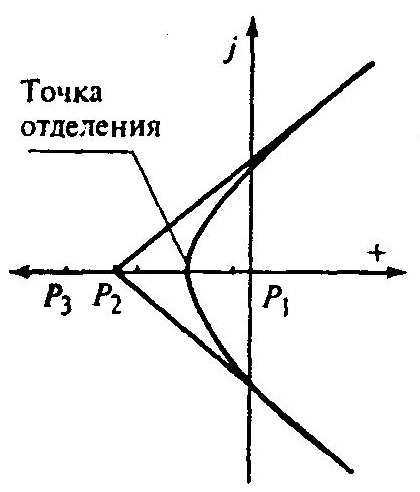
В точке отделения появляется два комплексно-сопряженных корня и все корни с ростом К уходят в бесконечность.
Построение области устойчивости осуществляется в зависимости от двух параметров модели. Первый введенный параметр будет изменяться вдоль оси ординату, а второй — вдоль оси абсцисс х.
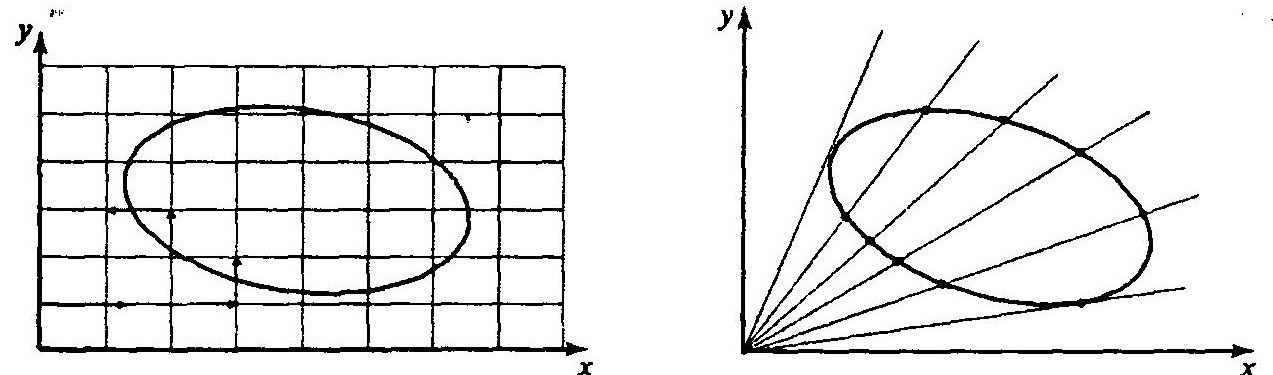
Построение области устойчивости может быть осуществлено или методом обхода границы или методом сканирования допустимой области вдоль лучей до нахождения точек границы (рисунок ниже).
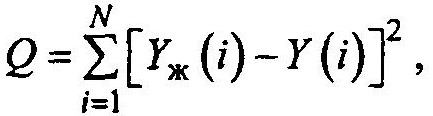
Параметрическая оптимизация в МАСЛИН реализуется вследствие выбора одного из методов (Гаусса, Зейделя, симплекс и Розенброка). Можно выбрать до пяти оптимизируемых параметров. Оптимизация может быть осуществлена по частотной или временной характеристике. Формирование критерия оптимизации реализуется подпрограммой KRIT. В качестве критерия используется квадратичный критерий. где Уж(i) — ордината желаемой характеристики; Y(i) — ордината характеристики, рассчитываемой при текущих значениях оптимизируемых параметров; N— количество точек.
Желаемая характеристика вводится последовательно с увеличением значений по оси X.
Программный комплекс МАСЛИН очень удобен и прост и не требует специальной программистской подготовки пользователя.