Мы рассмотрели основные математические модели непрерывных систем. Но при решении задач с применением ЭВМ (будь-то задача управления или задача моделирования) исследователь сталкивается с дискретными процессами, связанными как с квантованием по уровню, так и с квантованием по времени.

В цифровых системах управления влияние квантования по уровню, как правило, не рассматривают. Квантование по уровню вносит малые погрешности, так как сигналы изменяются в широком диапазоне, а ЭВМ обладает большой разрядной сеткой. Разрядность преобразователей непрерывных сигналов выбирается так, чтобы их погрешность квантования была меньше статических и динамических ошибок датчиков. Обычно бывает достаточно десять двоичных разрядов, что дает относительную погрешность в 0,1 %. При моделировании систем на ЭВМ с большей разрядностью тем более обосновано пренебрежение квантованием по уровню. Поэтому для рассматриваемых задач важным является квантование по времени.

Последовательность значений независимой переменной представляется в этом случае в виде t_n, (n = 0,1,2,…). Приращение независимой
переменной — разность между (t_n ) и (t_n-1): τ_n = (t_n — t_n-1). Если τ_n одинаково для всех n, то при одинаковых приращениях независимой переменной τ имеем t_n=nτ (n = 0,1,2,…).

Зависимая переменная может быть представлена в виде x_n=x(t_n) = х(nτ) , а последовательность значений зависимой переменной в виде {x_n} = [x₀, x₁, x₂,…,x_n,…].

При цифровом моделировании систем, описываемых дифференциальными уравнениями, производные этих уравнений аппроксимируются различными конечно-разностными операторами. Например, производная может быть представлена следующим выражением

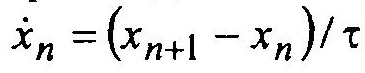
С уменьшением величины τ точность аппроксимации увеличивается. Такой подход позволяет получать разностные уравнения.

Комментарии запрещены.