Образовательный блог – всё для учебы

При моделировании надо избегать операции дифференцирования. Дифференцирование подчеркивает, усиливает шумы, помехи, содержащиеся в сигналах. Для того, чтобы избежать дифференцирования (у нас дифференцируется входной сигнал U), перестроим полученную схему эквивалентным образом. Составляющую с первой производной по U можно эквивалентно заменить просто на U, если подадим его на выход первого интегратора со своим коэффициентом b₁. Аналогично можно поступить со второй производной входного сигнала.
Для сокращения времени рассмотрим эквивалентные преобразования, связанные с максимальной, второй производной входного сигнала, а по другим составляющим приведем результат в окончательной эквивалентной схеме. Тогда в качестве исходной схемы рассматриваем схему, представленную на рис. 1.5.

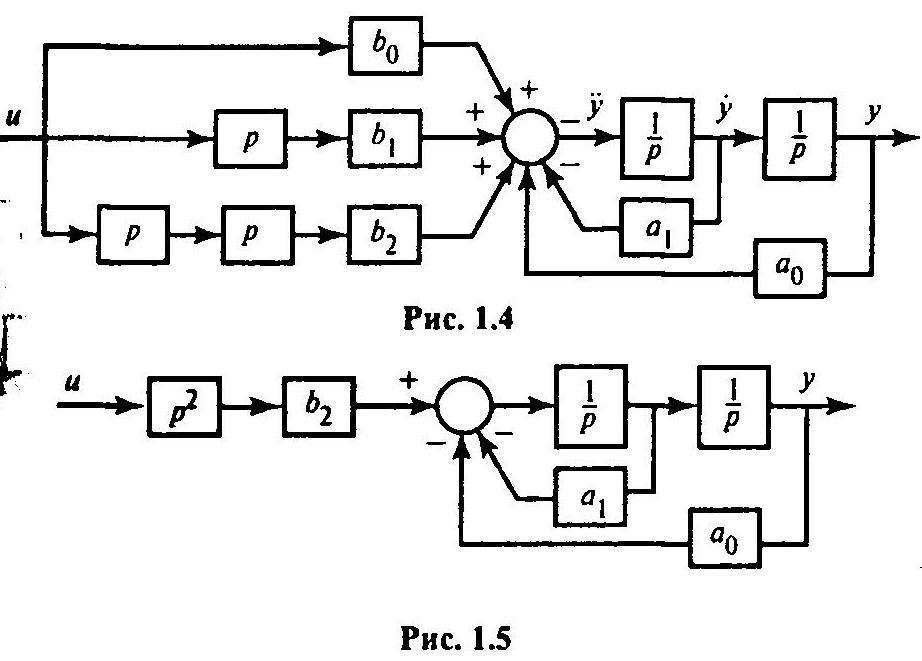
Для упрощения промежуточные переменные между входом и выходом опустим до получения окончательной эквивалентной схемы. Последовательность шагов преобразования этой схемы предложена на рис. 1.6, а-д.
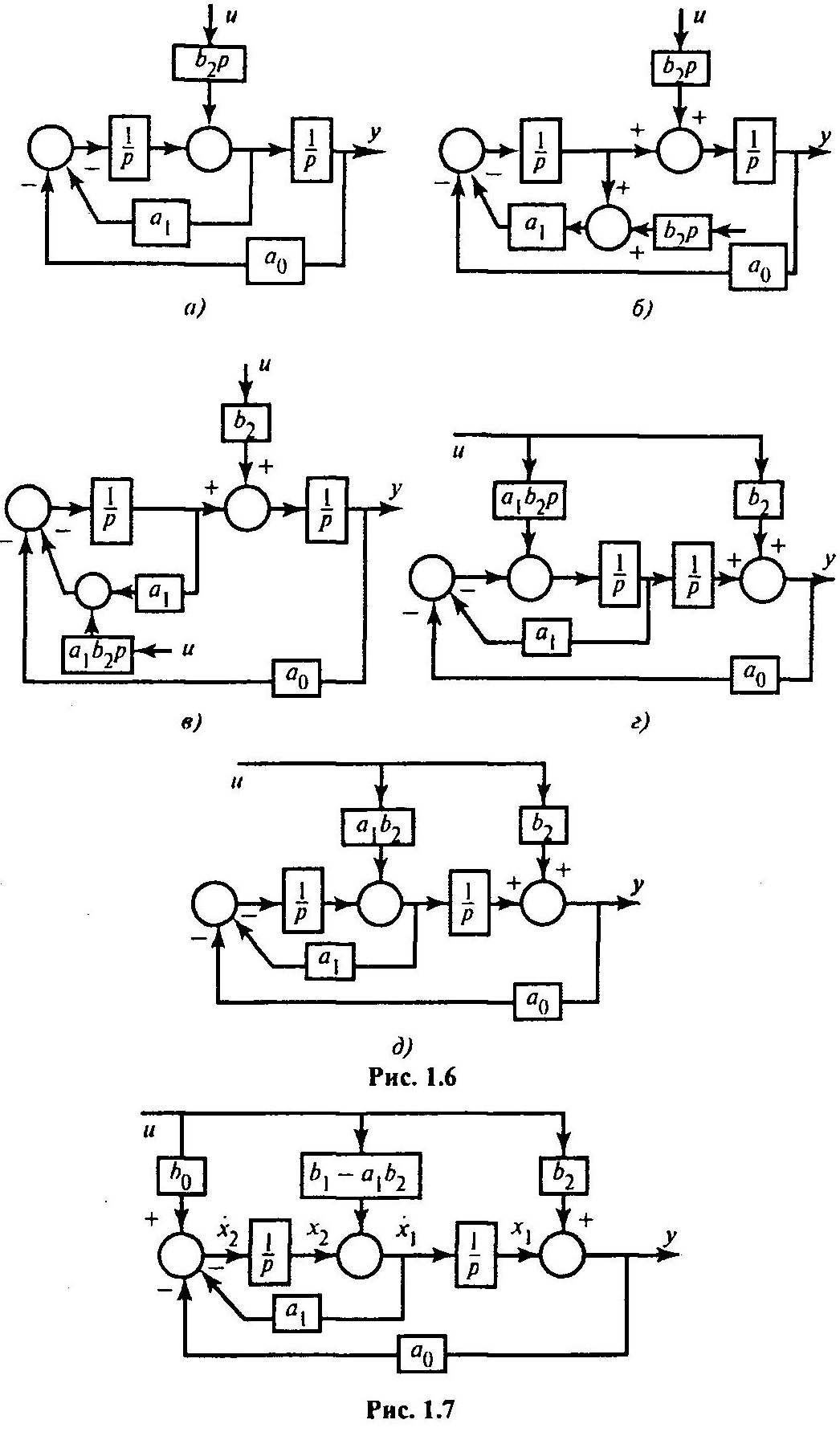
Проделав аналогичные преобразования со всеми составляющими входного сигнала (см. рис. 1.4), получим общую эквивалентную схему исходного дифференциального уравнения второго порядка без операции дифференцирования входного сигнала U (рис. 1.7).
Промежуточные переменные x₁, х₂ представляют собой переменные состояния. Если записать уравнения относительно производных переменных состояния, то получим уравнение системы в форме Коши:

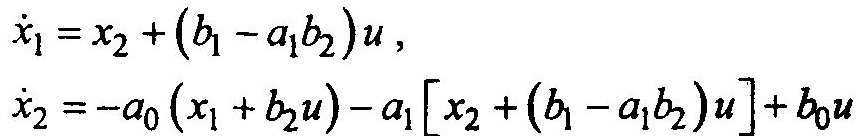
или

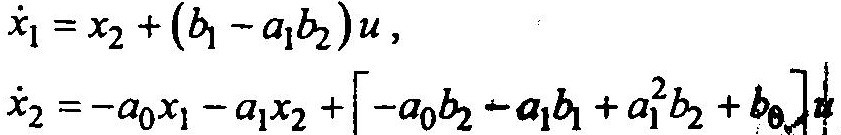
В векторно-матричной форме система (1.12) представляется в виде:

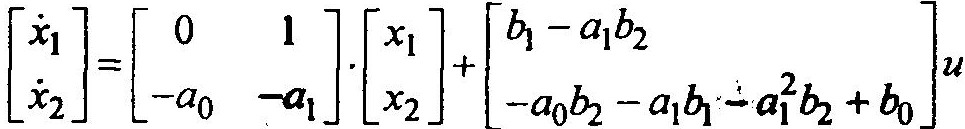
у = x₁ +b₂u.
В компактной форме эти уравнения для односвязных систем можно записать в виде:

х = Ах + Вu — уравнения состояния;
у = Сх + Du — уравнение наблюдения. (1.14)

Похожие записи

1. Нормальная форма записи уравнений состояния
2. Каноническая форма уравнений состояния
3. Z – преобразование
4. Математические модели непрерывных динамических систем
5. Модель в переменных состояния
6. Описание систем с помощью передаточных функций
7. Модели в пространстве состояний
8. Апериодическое звено в форме разностного уравнения
9. Математическая модель проектируемого устройства
10. Численное решение алгебраических уравнений
11. представления электронной схемы в виде физической системы
12. Стандартизованные формы представления моделей
13. Система VANTAGE при моделировании на VHDL
14. Инструментальное средство автоматизации моделирования непрерывных динамических систем
15. Геометрическая интерпретация уравнений возмущенного движения
16. Уравнения возмущенного движения
17. Рекуррентные уравнения, порядок уравнения, частное и общее решение