Математические модели непрерывных динамических систем
Динамические системы нашли широкое применение в различных областях человеческой деятельности. Они характеризуются зависимостью описывающих их переменных от времени, а также зависимостью выходного сигнала в отдельные моменты времени от предыстории входного. Здесь речь пойдет о математических формах представления моделей.
Динамические модели, описанные дифференциальными уравнениями, являются наиболее распространенным типом моделей.
Динамическую систему можно представить дифференциальным уравнением n-го порядка в виде
a(D)y(t) = b(D)u(t), (1.3)
где
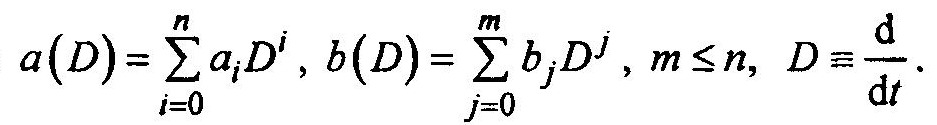
Широко используется представление динамических систем в форме Коши в виде n уравнений первого порядка. Действительно, если ввести новую переменную у1 (t) = y(t), то для любого 2 < к < n имеем Уk (t) = (Ук-1)’ (t)
Тогда от уравнения n-го порядка, записанного относительно высшей производной
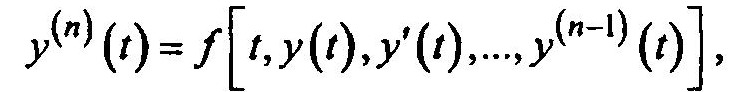
при t = t0 y(t0) = y10, y'(t0) = y20, … , y(n-1)(t0) = yn0 переходим к системе
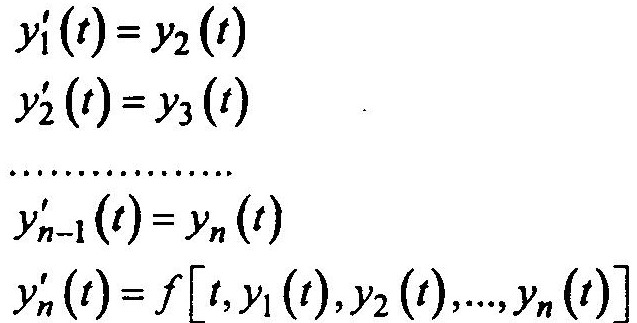
при начальных условиях y1(t0) = y10, y2(t0) = y20, …, yn(t0) = yn0
Это и есть система дифференциальных уравнений в нормальной форме Коши — совокупность n уравнений первого порядка.