Псевдослучайная двоичная последовательность и её основные свойства
Псевдослучайная двоичная последовательность (ПСДП) х[n] математически удовлетворяет некоторому линейному однородному разностному уравнению вида
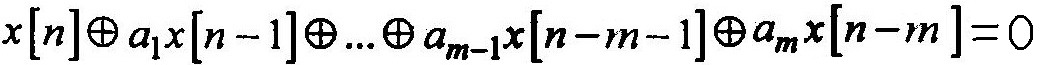
Псевдослучайная двоичная последовательность (1)
где а1, а2,…,аm, а также значения х[n] принадлежат множеству {0,1}. Символ плюсик в кружочке (суммирование) означает сложение по mod 2. Множество {0,1} образует конечное поле Галуа GF(2).
Для анализа свойств периодической последовательности, представляющей собой решение уравнения (1), используют Z-преобразование над конечным полем в форме:
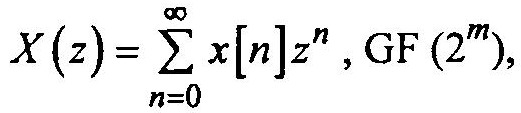
Z-преобразование (2)
где z — основание поля, а 2m — число элементов поля.
В случае произвольного числа уровней имеем GF(pm), где р — основание поля, а m — порядок поля или число элементов поля.
Применив преобразование (2) к уравнению (1), получим:
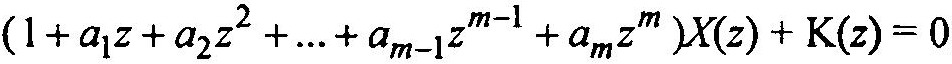
где P(z) = 1 + a1z + a2z2 +… + am-1zm-1] + amzm неизменно для данного уравнения и представляет собой характеристический полином, а K(z) — изменяемая часть и зависит от начальных условий.
Для получения двоичной последовательности х[n] можно на основе характеристического полинома построить генератор, представляющий собой регистр сдвига с логической обратной связью. Общую структурную схему такого генератора можно представить в виде
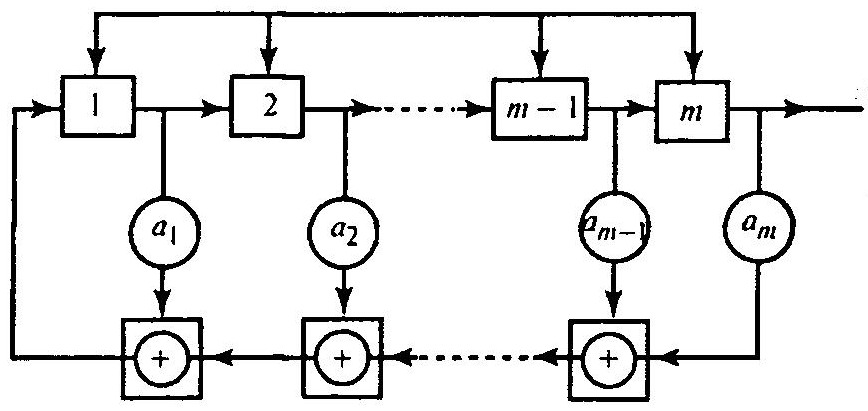
Структурную схема генератора двоичной последовательности х[n]
Генератор состоит из m запоминающих ячеек, схем сложения по mod 2 и умножения двоичного числа на коэффициенты а1,а2,…,аm.
Для задач представляют интерес последовательности максимальной длины — М-последовательности.
Из схемы генератора следует, что последовательность х[n] будет периодически повторяться. Поэтому М-последовательность — это последовательность с максимальным периодом.
Необходимым и достаточным условием обеспечения максимального периода последовательности х[n] является примитивность характеристического полинома, что означает:
1) характеристический полином неприводим, т.е. его нельзя представить в виде произведения полиномов более низкой степени, чем характеристический полином;
2) характеристический полином является делителем выражения z в степени сигма плюс сумма по модулю zσ⊕1 при σ = 2m — 1 и не является делителем этого выражения ни при каких других значениях σ < 2m — 1 {m — степень характеристического полинома, сигма — целое положительное число).
Здесь следует подчеркнуть, что каждое разностное уравнение порождает свой характеристический полином. В общем случае характеристический полином может иметь не один, а несколько примитивных полиномов. В литературе приводятся таблицы примитивных полиномов для характеристических полиномов разной степени. Примеры примитивных полиномов приведены ниже:
Степень полинома m — Примитивные полиномы
3 — z3+z+1, z3+z2+1
8 — z8+z4+z3+z2+1
31 — z31+z3+1
Отметим ряд интересных для наших целей свойств М- последовательностей:
1) период N = 2m-1 ;
2) в последовательности есть все комбинации двоичных символов кроме нулевой;
3) сумма по mod 2 М-последовательности с этой же М-последовательностью, сдвинутой на любое число тактов, кроме числа, равного периоду, является М-последовательностью того же вида, но со сдвигом;
4) автокорреляционная функция определяется соотношением
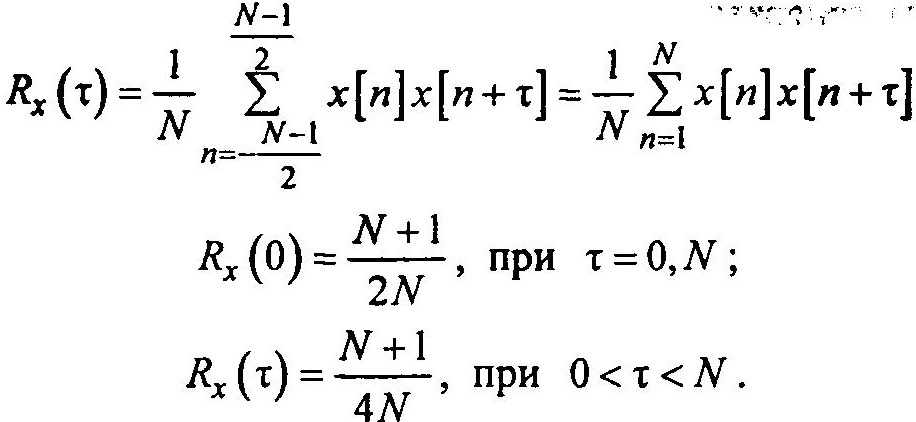
Часто вместо последовательности x[n] с элементами {0,1} удобно использовать М-последовательность с элементами {-1,1}. Для получения последовательности {-1,1} пропустим последовательное; через блок с функцией 2x[n] -1.
В этом случае
Rx(0) = 1, τ = 0, …, N, Rx(x) = -1/N, 0<τ
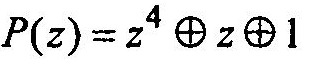
Вид примитивного полинома определяет структуру, схему регистра, на базе которого строится генератор.
Так как порядок примитивного полинома m=4, то генератор включает четыре запоминающие ячейки, причем суммируются по mod 2 лишь выходы первой и четвертой ячеек (так как в полином присутствуют лишь z и z4).
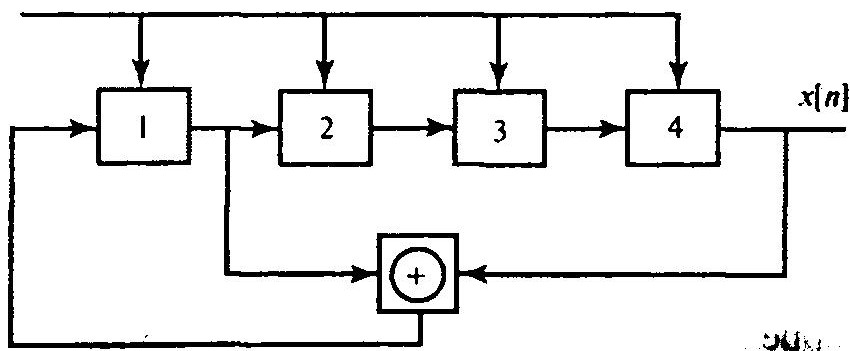
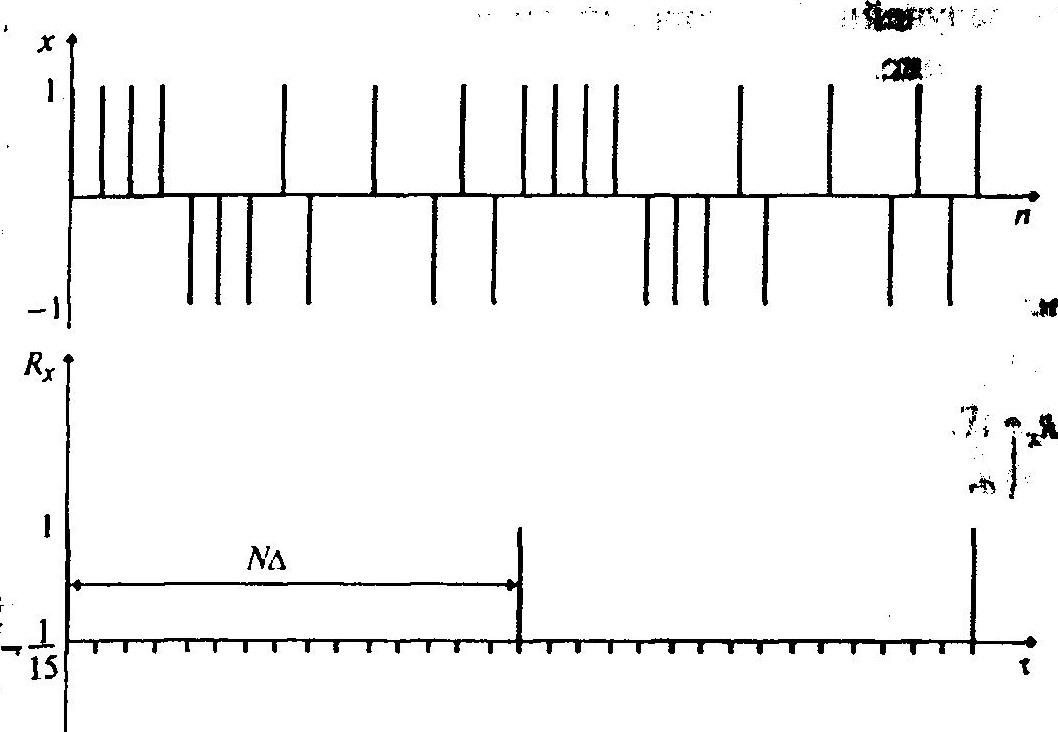
Длина этой последовательности N =2m — 1 = 15, т.е. период составит 15 тактов, что легко проверить. М-последовательность с элементами {-1,1} и её автокорреляционная функция для данного примера имеют вид (при определенных начальных условиях на регистре), представленный на рисунке выше.
При исследовании непрерывных систем пользуются псевдослучайными сигналами x(t), имеющими непрерывную зависимость от времени. Псевдослучайный двоичный сигнал (ПСДС) однозначно определяется М-последовательностью х[n]. Поэтому ПСДС обладает основными свойствами, присущими порождающей его М-последовательности.
Псевдослучайный двоичный сигнал получается пропусканием х[n] с элементами {-1,1} через формирующее устройство, имеющее релейную характеристику:
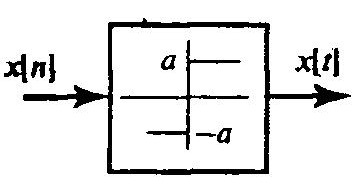
Псевдослучайный двоичный сигнал и его характеристики представлены на рисунке ниже.
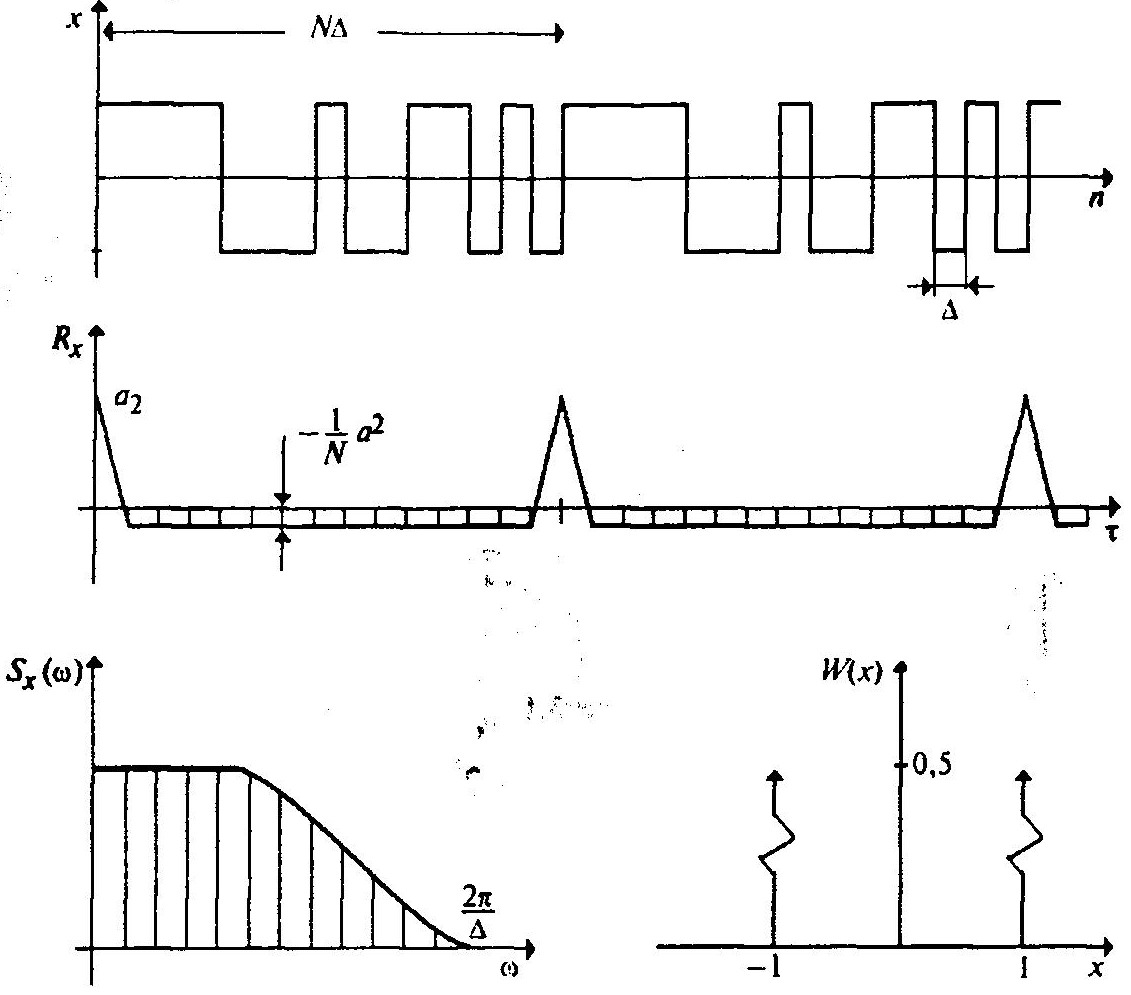
Псевдослучайный двоичный сигнал
Чем больше N и чем меньше δ, тем больше корреляционная функция ПСДС близка к δ-функции. Чем меньше δ, тем шире спектральная плотность ПСДС — Sx(w).