Каноническая форма уравнений состояния
В теории управления широко используется и каноническая форма представления в литературе. На эту форму лучше всего переходить с помощью передаточных функций.
Каноническая форма представления уравнений состояния зависит от типа корней характеристического уравнения. Особенно удобен такой переход при рассмотрении односвязных систем, не содержащих полиномов в числителе передаточной функции, представлением передаточной функции исследуемой системы в виде суммы элементарных дробей. При комплексных корнях получаются комплексные переменные состояния, и на практике этот случай не применяют.
Рассмотрим случай простых корней. Пусть исследуемая система имеет передаточную функцию вида
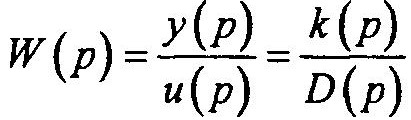
Для случая простых и кратных корней
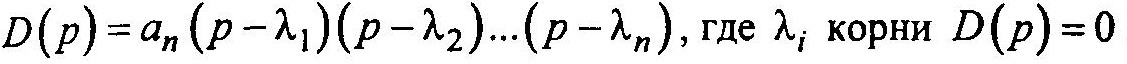
Тогда передаточную функцию можно записать в виде
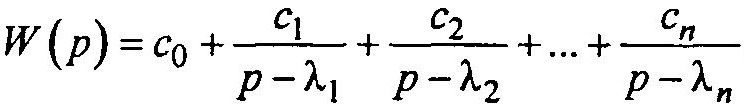
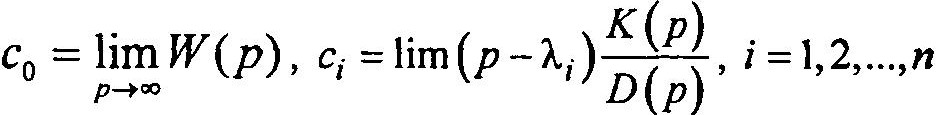
Представим выходную величину в виде
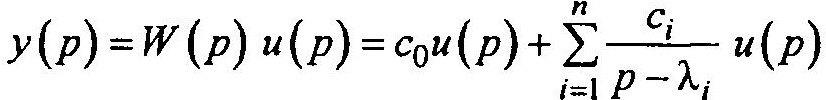
Соответствующая блок-схема представлена на рис. 1.10.
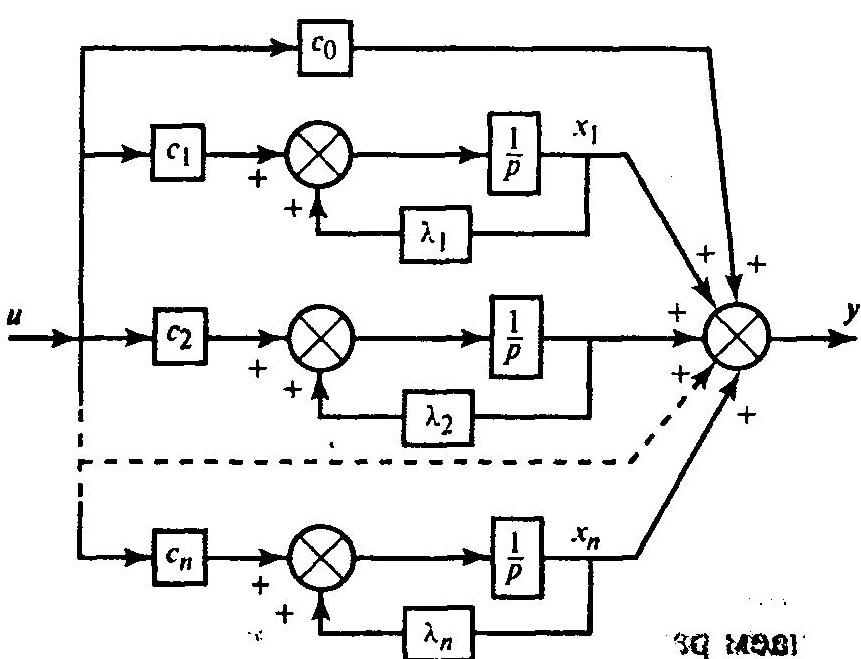
Рис. 1.10
Из схемы следует, что переменные состояния удовлетворяют следующим дифференциальным уравнениям первого порядка
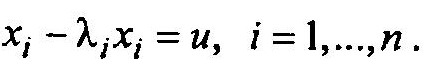
Уравнения в пространстве состояния принимают вид:
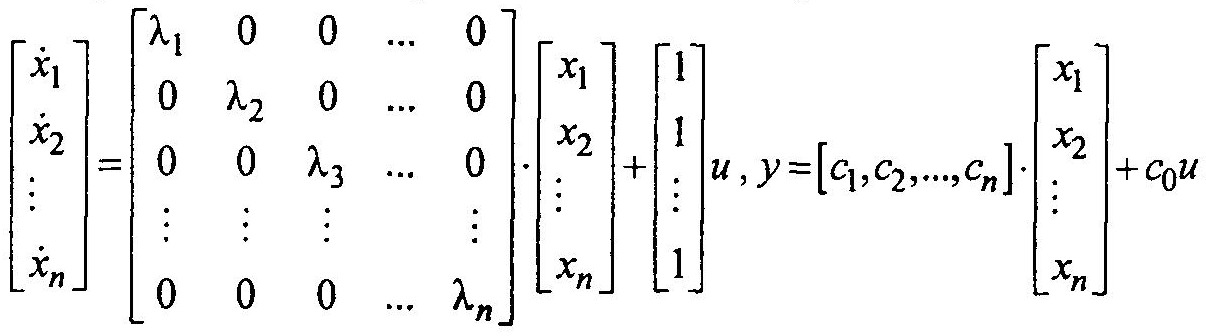
или в векторной форме:
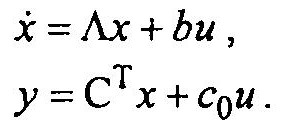
Здесь Л — диагональная матрица, состоит из собственных значений α1, α2,…, αn.
Так представляются уравнения состояния в канонической форме при простых корнях.