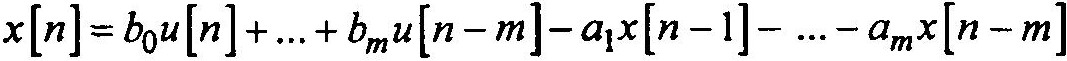Образовательный блог – всё для учебы

Приближенную модель апериодического звена в форме разностного уравнения можно получить из соответствующего дифференциального уравнения

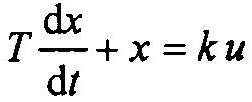
Заменяем дифференциалы приращениями на интервале квантования по времени

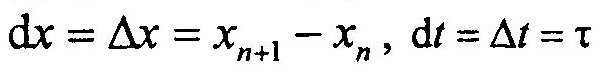
Тогда получим

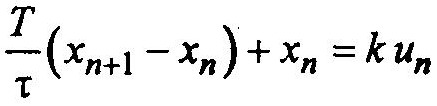
Перепишем последнее выражение в виде;



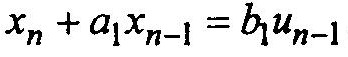
Получили линейное разностное уравнение первого порядка.
По аналогии можно записать линейное разностное уравнение
m-го порядка в виде:

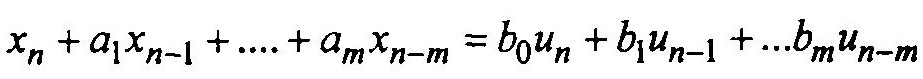
или

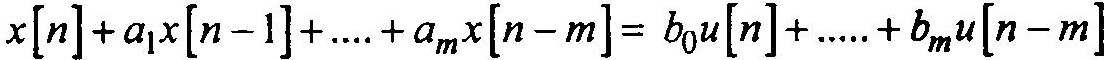
Величину выходного сигнала х[n] для любого n можно вычислить, если известны текущие значения входа u[n] и m предшествующих значений входа— u[n-1],…,u[n-m] и выхода — х[n-1],…,х[n-m] с помощью рекуррентной формулы

Похожие записи

1. Рекуррентные уравнения, порядок уравнения, частное и общее решение
2. Избавление от дифференцирования при моделировании
3. Z – преобразование
4. Математические модели непрерывных динамических систем
5. Линейные рекуррентные уравнения однородные и неоднородные с постоянными коэффициентами
6. Уравнения первого приближению
7. Уравнения возмущенного движения
8. Каноническая форма уравнений состояния
9. Линейные рекуррентные уравнения(ЛРУ) однородные и неоднородные с переменными коэффициентами
10. Модель в переменных состояния
11. Описание систем с помощью передаточных функций
12. Организация пакета прикладных программ идентификации динамических объектов
13. Характеристики коронного разряда между коаксиальными цилиндрами
14. Критерии Рауса-Гурвица и Льенара-Шипара
15. Программный комплекс для исследования линейных динамических систем
16. Инструментальное средство автоматизации моделирования непрерывных динамических систем
17. Алгоритмы получения сигналов с заданными статическими свойствами