Архив рубрики «Моделирование»
Основные показатели эффективности численного интегрирования дифференциальных уравнений
Автор: Рассмотрим основные показатели эффективности численного интегрирования дифференциальных уравнений.
Эффективность численного интегрирования, прежде всего, определяется точностью и устойчивостью вычислительного процесса.
Прочитать остальную часть записи »
Очереди в GPSS
Транзакты в процессе перемещения по модели могут задерживаться перед некоторыми блоками, если условия входа не выполняются. Примерами таких блоков из рассмотренных выше являются блоки:
• SEIZE (если ранее вошедший в этот блок транзакт не вошел в блок RELEAZE),
• ENTER (если требуемая текущим транзактом емкость памяти больше емкости свободного участка данной памяти),
• GATE и TEST (если в этих блоках не указан альтернативный выход и проверяемое условие не выполняется).
Прочитать остальную часть записи »
Численные методы интегрирования
Составление модели исследуемой системы соединением готовь программных модулей и воспроизведение сигналов, действующих на систему, является подготовительным шагом для имитационного исследования. Машинный эксперимент проводится в целях получения информации о характеристиках функционирования рассматриваемого объекта. Основная задача планирования машинных экспериментов — получение необходимой информации об исследуемой системе при ограничениях на ресурсы (затраты машинного времени, памяти и т.п.).
Прочитать остальную часть записи »
Память в GPSS
Память (STORAGE) представляет собой объект GPSS, обладающий определенной емкостью. Объекту STORAGE системы GPSS в реальных моделируемых системах могут соответствовать:
Прочитать остальную часть записи »
Алгоритмы получения сигналов с заданными статическими свойствами
В задачах имитационного моделирования систем, подверженных действию случайных сигналов, важное место принадлежит воспроизведению реально действующих сигналов. Задача заключается в еле дующем: располагая видом и параметрами корреляционной функции и закона распределения математически заданного или реально действующего сигнала (полученного на основе обработки реализаций по экспертным данным) разработать алгоритмы, позволяющие создавать модели случайных сигналов, имеющих близкие к ним соответствующие статические характеристики.
Прочитать остальную часть записи »
Устройства в GPSS: FACILITY
Устройство (FACILITY) в системе GPSS представляет собой объект, в котором могут выполняться операции обработки транзакта (обслуживания заявок).
Особенность устройства состоит в том, что в любой данный момент времени оно может быть занято лишь одним транзактом. Если устройство занято и текущий транзакт не может войти в устройство, то транзакт прекращает перемещение по модели (становится заблокированным) и ожидает освобождения данного устройства. Занятие и освобождение устройства моделируют соответственно блоки
SEIZE A
RELEASE А
где A – имя или номер устройства.
Прочитать остальную часть записи »
Псевдослучайная двоичная последовательность и её основные свойства
Псевдослучайная двоичная последовательность (ПСДП) х[n] математически удовлетворяет некоторому линейному однородному разностному уравнению вида
Псевдослучайная двоичная последовательность (1)
где а1, а2,…,аm, а также значения х[n] принадлежат множеству {0,1}. Символ плюсик в кружочке (суммирование) означает сложение по mod 2. Множество {0,1} образует конечное поле Галуа GF(2).
Прочитать остальную часть записи »
Алгоритм перемещения транзактов – алгоритм моделирования в системе gpss
Процесс моделирования ДС во времени проводится по шагам и начинается с установки в ноль таймера (счетчика модельного времени) и генерации (порождения) транзактов в блоках GENERATE (присваивание значений СЧА транзакту выполняется автоматически в соответствии с описанием работы этого блока).
Прочитать остальную часть записи »
Случайные сигналы и способы их получения
Случайным сигналом называется такой, который при каждом фиксированном значении аргумента является случайной величиной. В реальных условиях большая часть сигналов и воздействий представляют собой такие случайные функции. Несмотря на многообразие методов генерирования случайных процессов, их можно разделить на две группы:
Прочитать остальную часть записи »
Объекты системы моделирования и средства их реализации. Транзакты
В языке GPSS применяются два класса объектов:
— статические объекты, которые объявляются в тексте программы: УСТРОЙСТВА (FACility), ПАМЯТИ (STOrage), ОЧЕРЕДИ (QUEue), ЛОГИЧЕСКИЕ КЛЮЧИ (LOGic), ПЕРЕМЕННЫЕ (VARiable), ЯЧЕЙКИ (полнословные FSV, полу-словные HSV), ФУНКЦИИ (FUNction), ТАБЛИЦЫ (TABle);
— динамические, порождаемые в процессе моделирования: ТРАНЗАКТЫ (XAC).
Прочитать остальную часть записи »
Основные детерминированные воздействия
Проблемно-ориентированные модульные системы программирования позволяют быстро формировать из компонентов модель исследуемой системы. Однако формирование модели является лишь начальным этапом исследования. Для его реализации необходимо обеспечить целый комплекс дополнительных средств.
Прочитать остальную часть записи »
Структура программы на языке GPSS
Идеи, заложенные в систему моделирования GPSS, относятся к семидесятым годам, когда высокоуровневые языки программирования по существу только начали развиваться. Поэтому с точки зрения программиста модель на языке GPSS по структуре близка к программе на языке ассемблера: каждое предложение занимает одну строку, содержащую либо управляющий оператор (например, REALLOCATE, SIMULATE, START, END), либо объявление имени объекта, либо функциональный оператор (БЛОК).
Прочитать остальную часть записи »
Язык и система моделирования GPSS
GPSS — General Purpouse Simulation System — это система моделирования общего назначения. Она предназначена для моделирования дискретных систем (ДС) на уровне структуры и информационных (или материальных) потоков в системе, т. е. когда работу ДС можно задать множеством состояний и графом переходов системы из одного состояния в другое. Изменение состояния системы называется событием.
Прочитать остальную часть записи »
Краткий обзор современных языков и систем моделирования
При моделировании динамических систем на ЭВМ в первую очередь необходимо представить их математические модели в виде программ. Следовательно, большое значение при реализации модели имеет правильный выбор языка моделирования.
Язык моделирования должен обеспечить:
1) удобство описания процесса функционирования системы,
2) удобство ввода исходных данных,
3) составление и варьирование структуры, параметров модели,
4) реализуемость как детерминированного, так и статистического моделирования.
Прочитать остальную часть записи »
Пакеты прикладных программ
Основу многих современных систем моделирования (как и САПР) составляют пакеты прикладных программ (ППП). Комплексные программные системы могут объединять несколько ППП.
Пакеты прикладных программ могут быть:
• объектно-зависимыми, проблемно-ориентированными на определенную предметную область;
• объектно-независимыми, методоориентированными (инвариантными), т.е. могут использоваться при моделировании и решении задач из различных предметных областей.
Применение таких методоориентированных ППП часто менее эффективно:
• в них не учитывается специфика задач конкретной предметной области;
• требуется достаточно высокая математическая подготовка пользователя, так как при использовании объектно-независимых ППП необходима специальная предварительная подготовка задачи в соответствии с особенностями применяемого метода.
Прочитать остальную часть записи »
Реализация непроцедурных систем программирования
Реализация НСП может быть достигнута лишь за счет их предметной (проблемной) ориентации, позволяющей построить в памяти компьютера описание модели предметной области (МПО).
Модель предметной области должна содержать множество (словарь) категорий (идентификаторов объектов), используемых в данной предметной области. Из сказанного следует, что НСП должна содержать терминологический словарь предметной области, a R(x) получается с помощью законов, известных в данный момент в предметной
области.
Прочитать остальную часть записи »
Функциональные блоки систем имитационного моделирования и их программная реализация
Исходя из особенностей имитационного моделирования, наиболее рационально строить модель по блочному принципу. Основные группы функциональных блоков были упомянуты ранее.
Каждый блок выполняет определенную законченную функцию, поэтому он достаточно автономен и должен иметь минимальное количество связей с другими блоками. Разумеется, что каждому такому блоку соответствует своя, как правило, типовая математическая модель. Например, это могут быть модели типовых динамических звеньев, модели генерации сигналов, схемы вероятностных и конечных автоматов, схемы массового обслуживания, которые достаточно точно описывают основные особенности реальных процессов.
Прочитать остальную часть записи »
Укрупненная архитектура имитационной системы
Система имитационного моделирования может рассматриваться как машинный аналог сложного реального процесса.
На рис. 2.1 представлена укрупненная архитектура имитационной системы. Имитационная система должна иметь интеллектуальный интерфейс, т.е. обеспечивать удобное и эффективное взаимодействие широкого пользователя с ЭВМ.
Такой интеллектуальный интерфейс должен содержать средства дающие возможность:
Прочитать остальную часть записи »
Реализация имитационного моделирования
Имитационная модель задается из совокупности моделей отдельных компонентов системы и связей между ними. Но составление моделей — не самоцель. Модель требуется для реализации машинных экспериментов. Таким образом, после создания модели системы из компонентов надо иметь средства для организации различных экспериментов с ней. Кроме того, необходимо в удобном виде представить результаты эксперимента для их анализа.
Прочитать остальную часть записи »
Z — преобразование
Для описания и анализа дискретных систем, решения разностных и рекуррентных уравнений используется Z -преобразование.
Z-преобразование применяют к сигналу, квантованному по времени (к дискретным значениям непрерывного сигнала).
Z -преобразование определяется как сумма отрицательных степеней комплексной переменной z с помощью соотношения:
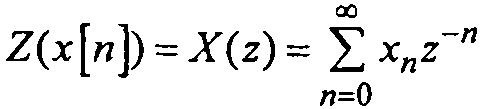(1.18)Прочитать остальную часть записи »
Апериодическое звено в форме разностного уравнения
Приближенную модель апериодического звена в форме разностного уравнения можно получить из соответствующего дифференциального уравнения
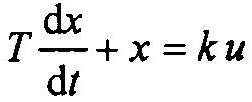
Заменяем дифференциалы приращениями на интервале квантования по времени
Прочитать остальную часть записи »
Дискретное представление динамических систем
Мы рассмотрели основные математические модели непрерывных систем. Но при решении задач с применением ЭВМ (будь-то задача управления или задача моделирования) исследователь сталкивается с дискретными процессами, связанными как с квантованием по уровню, так и с квантованием по времени.
Прочитать остальную часть записи »
Стандартизованные формы представления моделей
Каноническая форма приводит к удобной диагональной матрице коэффициентов. Каноническая форма, как и нормальная, представляет собой стандартизованную форму записи моделей в пространстве состояний.
По сути, нормальная форма записи (входной сигнал и n-1 его производные) уравнений состояния представляет собой описание системы в фазовом пространстве. Фазовые координаты выступают как переменные состояния (и наоборот). Фазовый вектор является специфическим вектором состояния.
Прочитать остальную часть записи »
Каноническая форма уравнений состояния
В теории управления широко используется и каноническая форма представления в литературе. На эту форму лучше всего переходить с помощью передаточных функций.
Каноническая форма представления уравнений состояния зависит от типа корней характеристического уравнения. Особенно удобен такой переход при рассмотрении односвязных систем, не содержащих полиномов в числителе передаточной функции, представлением передаточной функции исследуемой системы в виде суммы элементарных дробей. При комплексных корнях получаются комплексные переменные состояния, и на практике этот случай не применяют.
Прочитать остальную часть записи »
Нормальная форма записи уравнений состояния
В общей эквивалентной схеме сигналы в обратных связях не являются собственно переменными состояния — с точек разветвления на обратные связи поступают переменные состояния х, и плюс еще что-то. Для получения нормальной формы надо так преобразовать схему, чтобы точки съема были бы непосредственно с выхода интеграторов, так как именно на выходе интеграторов имеют место переменные состояния x1 и х2. Для этого перенесем сумматоры после каждого интегратора через точки разветвления (узлы или точки съема). Если опустить простейшие преобразования и ввести обозначения:
Прочитать остальную часть записи »
Избавление от дифференцирования при моделировании
При моделировании надо избегать операции дифференцирования. Дифференцирование подчеркивает, усиливает шумы, помехи, содержащиеся в сигналах. Для того, чтобы избежать дифференцирования (у нас дифференцируется входной сигнал U), перестроим полученную схему эквивалентным образом. Составляющую с первой производной по U можно эквивалентно заменить просто на U, если подадим его на выход первого интегратора со своим коэффициентом b1. Аналогично можно поступить со второй производной входного сигнала.
Для сокращения времени рассмотрим эквивалентные преобразования, связанные с максимальной, второй производной входного сигнала, а по другим составляющим приведем результат в окончательной эквивалентной схеме. Тогда в качестве исходной схемы рассматриваем схему, представленную на рис. 1.5.
Прочитать остальную часть записи »
Модель в переменных состояния
Исходными уравнениями являются дифференциальные уравнения динамических систем. Рассматриваемый метод представляет собой метод понижения порядка дифференциального уравнения посредством последовательного интегрирования.
В результате получаются схемы, в основе которых число интеграторов равно порядку дифференциального уравнения.
Прочитать остальную часть записи »
Модели в пространстве состояний
Для описания многосвязных систем наиболее адекватными являются модели в пространстве состояний. Решение системы дифференциальных уравнений зависит от произвольных постоянных, определяемых из начальных условий (т.е. в момент времени t0). Эти начальные условия и представляют состояние системы в момент t0.
Прочитать остальную часть записи »
Описание систем с помощью передаточных функций
В теории автоматического управления используется описание системы с помощью передаточных функций. Передаточная функция получается в результате непрерывного преобразования Лапласа соответствующего дифференциального уравнения.
При нулевых начальных условиях дифференциальные уравнения и передаточные функции взаимно-однозначно связаны.
Передаточная функция системы автоматического управления может быть представлена отношением полиномов вида
Прочитать остальную часть записи »
Математические модели непрерывных динамических систем
Динамические системы нашли широкое применение в различных областях человеческой деятельности. Они характеризуются зависимостью описывающих их переменных от времени, а также зависимостью выходного сигнала в отдельные моменты времени от предыстории входного. Здесь речь пойдет о математических формах представления моделей.
Прочитать остальную часть записи »