В общей эквивалентной схеме сигналы в обратных связях не являются собственно переменными состояния — с точек разветвления на обратные связи поступают переменные состояния х, и плюс еще что-то. Для получения нормальной формы надо так преобразовать схему, чтобы точки съема были бы непосредственно с выхода интеграторов, так как именно на выходе интеграторов имеют место переменные состояния x₁ и х₂. Для этого перенесем сумматоры после каждого интегратора через точки разветвления (узлы или точки съема). Если опустить простейшие преобразования и ввести обозначения:

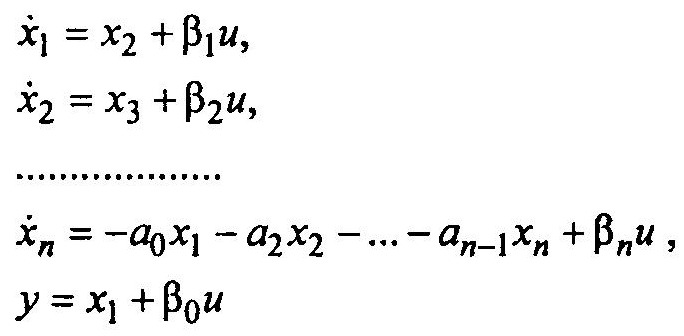
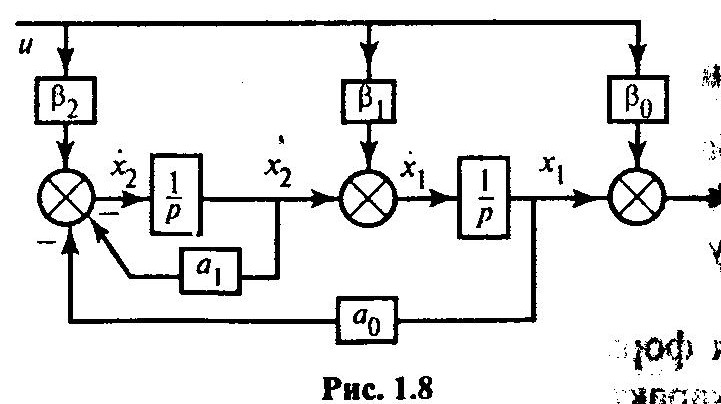
то можно преобразованную структуру представить в нормальной форме (рис. 1.8).

Обобщим этот результат на общий случай, когда n = m (когда степени левой и правой частей исходного дифференциального уравнения равны, рис. 1.9).

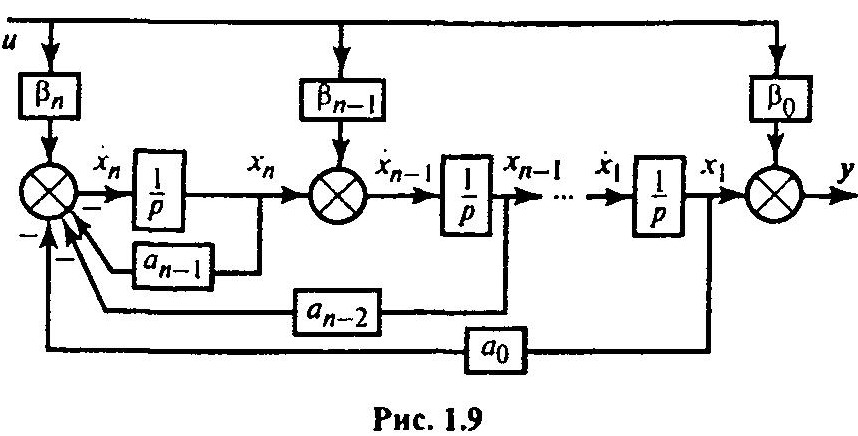
Из полученной схемы следуют уравнения:

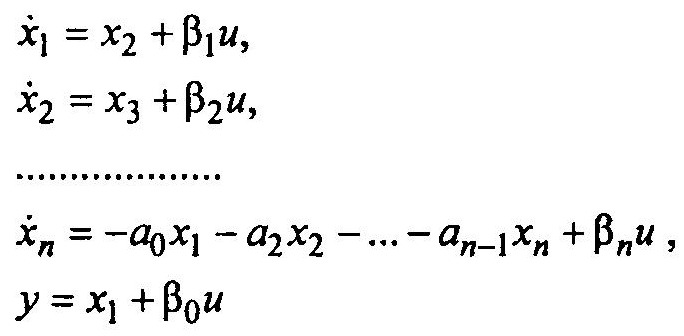
Или в векторно-матричной форме:

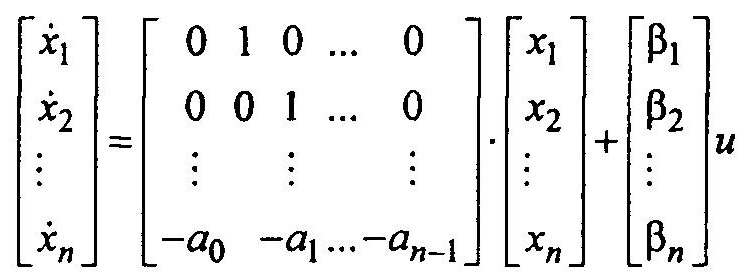
Таким образом имеем нормальную форму представления уравнений состояния.

При нормальной форме получается простая структура квадратичной матрицы коэффициентов А, что снижает вычислительные трудности при анализе моделей.

Комментарии запрещены.