Модели в пространстве состояний
Для описания многосвязных систем наиболее адекватными являются модели в пространстве состояний. Решение системы дифференциальных уравнений зависит от произвольных постоянных, определяемых из начальных условий (т.е. в момент времени t0). Эти начальные условия и представляют состояние системы в момент t0.
Состояние динамической системы определяется наименьшим набором параметров, которые необходимо задать в начальный момент для того, чтобы правильно предсказать дальнейшее поведение системы при известном входном воздействии. Если, например, рассматривается система дифференциальных уравнений n-го порядка, то для получения однозначного и правильного решения надо располагать числом переменных состояния, равным n. Этими переменными состояния могут быть значения самой переменной и (n-1) ее производных.
Общего определения понятия состояния системы нет, так как для каждой реальной системы оно различно. Но выбирают переменные состояния так, чтобы они имели определенный физический смысл. И еще — выбор переменных состояния не является однозначным. Это говорит о том, что для одного и того же объекта могут быть выбраны различные наборы переменных состояния, а значит и различные описания объекта, т.е. одна и та же система может иметь несколько векторов состояния.
При представлении через переменные состояния мы как бы привлекаем дополнительные промежуточные координаты (помимо входных и выходных переменных) для описания поведения системы. Это позволяет устранить неоднозначность между управляющими воздействиями и поведением выходных переменных.
Другими словами, переменные состояния обеспечивают автоматический учет начальных условий.
Для получения уравнений в переменных состояния (или в пространстве состояний) представим исследуемый объект в виде «черного ящика» с основными группами переменных (рис. 1.2), где uj—управляющие, входные воздействия, вектор u = {u1,u2,…,ur}; yq — управляемые, выходные переменные, вектор у = {у1,у2,…,уm}; xi—промежуточные переменные; вектор х = {х1,х2,…,хn} переменные состояния.
В случае односвязных линейных систем имеем одно входное воздействие u и одну выходную переменную у.
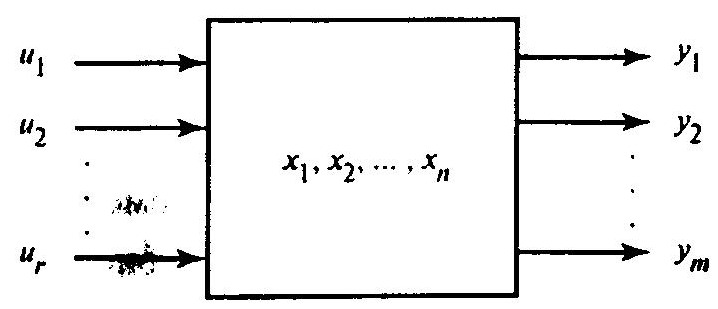
Рис. 1.2
Нормальная форма уравнений в этом случае записывается в виде
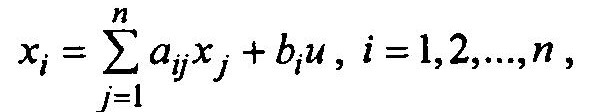 (1.7)
(1.7)где аi,j, bi — постоянные коэффициенты (могут быть и равны 0). Выходной сигнал (называют его наблюдаемым) у(t) выражается через переменные состояния соотношением
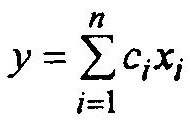 (1.8)
(1.8)где ci —постоянные коэффициенты.
Раскрывая записи уравнений (1.7) и (1.8), можно представить их в матричной форме:
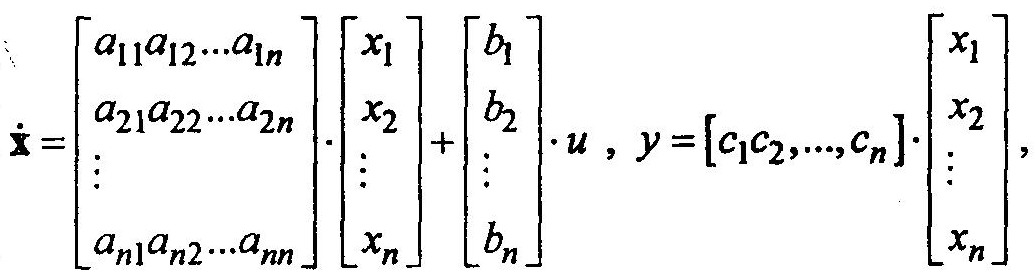 (1.9)
(1.9)Или компактной записи
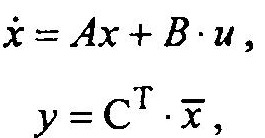 (1.10)
(1.10)где х — вектор состояния, матрица-столбец размерности
n х 1; С — матрица-столбец размерности 1 х n ; А — квадратная матрица размерности n х n с элементами аi,j; В — матрица-столбец размерности
n х 1.
В самом общем случае, когда рассматривается многосвязная система, уравнения (10) принимают вид:
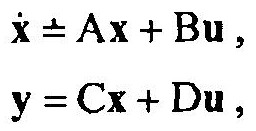
где В, С и D — прямоугольные матрицы размерности nхr, mхn и mхr соответственно.
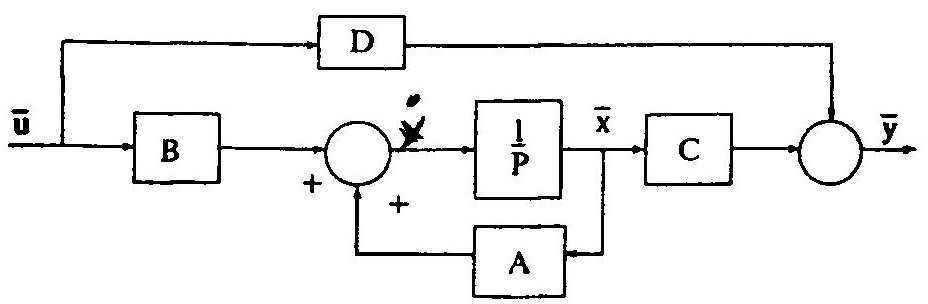
Рис. 1.3
Системе уравнений (1.11) можно поставить в соответствие векторную структурную схему системы в пространстве состояний, представленную на рис. 1.3.
В случае нестационарных систем матрицы коэффициентов являются функциями времени A(t), В(t), С(t) и D(t).
Выше было сказано, что одна и та же система может иметь несколько различных векторов состояния. Однако любые уравнения в переменных состояния одной и той же системы, связаны между собой однозначно.
Наиболее распространенными формами записи уравнений состояния являются нормальная и каноническая.