Основные показатели эффективности численного интегрирования дифференциальных уравнений
Рассмотрим основные показатели эффективности численного интегрирования дифференциальных уравнений.
Эффективность численного интегрирования, прежде всего, определяется точностью и устойчивостью вычислительного процесса.
Ошибки численного интегрирования
Источником погрешностей результатов численного интегрирования являются:
1) приближенная (неточная) математическая модель изучаемого реального объекта (системы);
2) численные методы решения на ЭВМ (они являются приближенными);
3) программная реализация методов может добавить свои ошибки.
Поэтому важнейшим показателем численного интегрирования является точность, которая оценивается погрешностью, величиной ошибки e(t) = yt(t) — y(t), где yt(t) —точное решение, которое может быть известно, y(t) — приближенное машинное решение.
Вычислительная погрешность складывается из следующих составляющих:
• погрешности методической, обусловленной приближенностью метода за счет аппроксимации, усечения (она связана с заменой дифференциальных уравнений их разностными аналогами);
• погрешности округления, обусловленной разрядностью сетки ЭВМ, конечной длиной машинного слова;
• ошибки накопления за счет суммирования от шага к шагу вычисления.
В общем случае оценить погрешность невозможно, если нет точного решения (в случае тестовых специально подобранных задач).
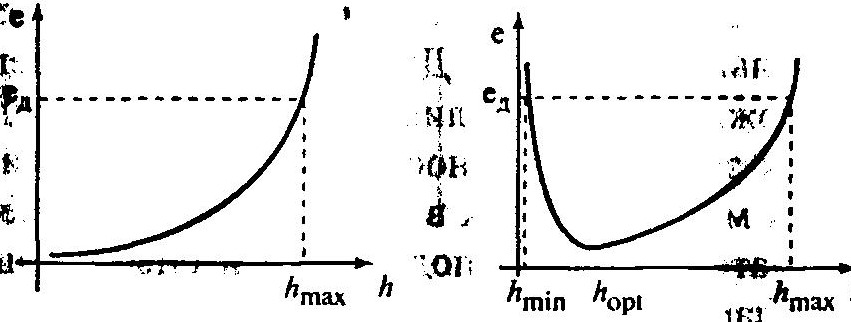
Устойчивость численного интегрирования (числовая неустойчивость). Поскольку погрешность от шага к шагу накапливается, то вычислительный процесс может стать неустойчивым. Так как погрешность зависит от величины шага, то при решении каждой конкретной задачи существует свой допустимый шаг интегрирования ед (рис. ниже). Превышение критической величины шага приводит к переполнению разрядной сетки и останову ЭВМ. Катастрофический рост погрешности является свидетельством потери числовой устойчивости, свидетельством неустойчивости вычислительного процесса.
Отметим, что устойчивость численных методов интегрирования может нарушиться не только при превышении hmax, но и при малых значениях h, если коэффициент усиления исследуемой системы велик.
При решении задач автоматического управления и в других областях исследователи встречаются с решением так называемых жестких систем дифференциальных уравнений. В жестких задачах возникают трудности с выбором шага h. Несмотря на существенный отрезок медленного изменения искомой функции, приходится выбирать мелкий шаг.
Попытки увеличить шаг в таких системах приводят к росту погрешности и неустойчивости процесса решения. Эта особенность определяется не тем или иным численным методом, а особенностями задачи Коши.
Система дифференциальных уравнений называется устойчивой и жесткой, если ее собственные значения (корни характеристического уравнения) характеризуются свойствами:
Re pi<0, max|pi| >> min|pi|
Обычно при формировании модели малыми параметрами (например, постоянными времени) пренебрегают, но есть системы для которых этого нельзя делать. К ним относятся системы с несколькими каналами управления, среди которых есть и быстрый и медленный каналы. Примерами таких систем могут служить автопилот самолета, процессы в ядерных реакторах и др.
Для решения вопроса о жесткости рассматриваемой системы вычисляют число жесткости:
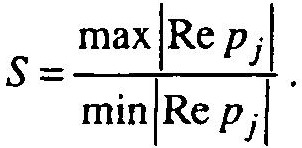
Если S>>1 (в тысячи и более раз), то система является жесткой. В общем случае, матрица рассматриваемой системы является сильно разреженной (имеет нулевые или близкие к нулям элементы).
Для решения жестких систем используют специальные, так называемые А-устойчивые методы численного интегрирования, которые обеспечивают устойчивость при
h > 0. Поиск эффективных А-устойчивых методов решения жестких задач продолжается. Сегодня популярным и известным является метод Гира. По методу Гира разработаны соответствующие программы.
Применение абсолютно устойчивых методов позволяет за счет увеличения шага существенно сократить время интегрирования.
Быстрое развитие ЭВМ расширяет круг решаемых задач численными методами. Появляются новые численные методы. Поэтому трудно дать рецепты к решению всех возможных реальных задач, так как нет универсальных методов. Для выбора метода решения конкретной задачи можно опираться лишь на общие рекомендации, а решающим является знание особенностей решаемой задачи и возможностей численных методов. Успех в прикладной науке требует достаточно хорошей математической подготовки и опыта решения задач численными методами.