Пример 1. Найти положения равновесия нелинейной системы и исследовать их устойчивость с помощью теорем Ляпунова об устойчивости по первому приближению
x^• = a x — c x y, c≠0
y^• = — by + d x y, d≠0.
Показать, что в зависимости от знаков параметров a, b выводы об устойчивости различные.

Решение: Данная система имеет два положения равновесия (особые точки)
x₁ = 0, y₁ = 0,
x₂ = b/d, y₂ = a/c.

Введем отклонения от положений равновесия
z₁ = x — x_k, z₂ = y — y_k, (k=1,2).

Тогда уравнения первого приближения около положений равновесия примут вид:
z₁^• = (a — cy_k) z₁ — cx_k z₂,
z₂^• = dy_k z₁ + (- b + dx_k) z₂.

Для первого положения равновесия уравнения первого приближения таковы
z₁^• = a z₁,
z₂^• = — bz₂
;
Соответствующее характеристическое уравнение имеет вид (λ — a)(λ + b) = 0.
Для второго положений равновесия уравнения первого приближения следующие
u₁^• = — (cb/d) u₂,
u₂^• = (ad/c) u₁,
а характеристическое уравнение имеет вид λ₂ + ab = 0.

Путем анализа корней характеристических уравнений можно сделать следующие выводы:

1. При a>0, b>0 нулевое положение равновесия x₁ = 0, y₁ = 0 исходной нелинейной системы неустойчиво («грубая» особая точка – седло, см. замечание ниже), поскольку существует корень характеристического уравнения, лежащий в правой полуплоскости λ₁=-a>0. Для второго положения равновесия x₂, y₂ характеристическое уравнение имеет два чисто мнимых корня (Re λ_1,2 = 0). В этом случае имеем критический случай исследования устойчивости по Ляпунову, т.е. об устойчивости второго положения равновесия x₂, y₂ ничего сказать нельзя –
нужно исследовать полные нелинейные уравнения. Численный анализ исходной нелинейной системы показывает, что при любых начальных условиях x₀>0, y₀>0 движение
изображающей точки происходит по замкнутым фазовым траекториям вокруг второй особой точки x₂, y₂ (рис.2.1). Следовательно, второе положение равновесия x₂, y₂ исходной нелинейной системы устойчиво (не асимптотически).

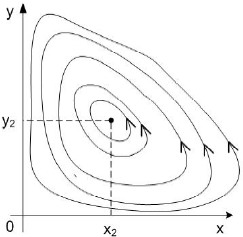
Рис.2.1 Фазовые траектории в случае a>0, b>0

2. При a<0, b>0 нулевое положение равновесия x₁ = 0, y₁ = 0 — асимптотически устойчиво («грубая» особая точка – устойчивый узел), поскольку оба корня характеристического уравнения лежат в левой полуплоскости (Re λ_1,2<0). Второе решение x₂, y₂ – неустойчиво («грубая» особая точка – седло), поскольку существует корень характеристического уравнения, лежащий в правой полуплоскости.

Замечание: Особая точка называется «грубой», если при добавлении в систему малых нелинейных слагаемых, тип особой точки не меняется.

Пример 2. Исследовать устойчивость по первому приближению нулевого решения системы
x^• = ω y + a x (x² + y²)^0.5 ,
y^• = — ω x + a y (x² + y²)^0.5,

Решение: Введем отклонения z₁ = x — x₁, z₂ = y — y₁ от нулевого положения равновесия x₁=0, y₁=0. Уравнения первого приближения около данного положения равновесия таковы:
z₁^• = ω z₂,
z₂^• = — ω z₁.

Характеристическое уравнение λ² + ω² = 0 имеет два чисто мнимых корня λ = ± iω.

Следовательно, имеем критический случай исследования устойчивости по Ляпунову.

Нулевое решение x₁= y₁= 0 линейной системы (при a = 0) просто устойчиво, но об
устойчивости нулевого решения x₁ = y₁ = 0 исходной нелинейной системы (при a ≠ 0) ничего сказать нельзя – нужно исследовать полные нелинейные уравнения.

Умножим первое уравнение на x, второе – на y и сложим уравнения. Получим x x^• + y y^•= a (x² + y²) (x² + y²)^0.5.

Если сделать замену x² + y² = r², то данное уравнение можно переписать в виде
r^• = a r².
Последнее уравнение легко интегрируется
r = r₀/[1 — a r₀ (t — t₀)].

Из анализа данного решения нелинейной системы нетрудно сделать выводы о том, что нулевое положение равновесия x₁ = y₁ = 0 нелинейной системы при a<0 асимптотически устойчиво (величина r стремится к нулю «по гиперболе»), а при a >0 — неустойчиво (величина r за конечное время уходит из малой окрестности нуля, а именно, при t → t₁=[ t₀ + 1/(ar₀)] стремится к бесконечности r → ∞.

Комментарии запрещены.