Рассмотрим задачу нелинейного программирования следующего
вида:

min x_n, где D = {x|g_i(x) ≥ 0, i = 1,2, …, m}. (7.97)

Относительно допустимой области D предположим, что она является односвязным замкнутым множеством. В отличие от задачи выпуклого программирования допустим, что множество D может не удовлетворять условию выпуклости. В этом случае задача (7.97) является задачей невыпуклого программирования и может иметь несколько локальных минимумов.

В общем виде задача невыпуклого программирования пока не имеет строгого математического решения. Однако в связи с тем, что данный класс задач часто встречается на практике, рассмотрим эвристический алгоритм, основная идея которого состоит в многократном применении некоторой модификации метода опорной гиперплоскости для разных значений внутренней точки x_B∈D.

Предположим, что имеется «внутреннее» множество допустимой области D₀ = {x|g_i(х) > 0, i = 1, 2, …, m}в котором определена начальная внутренняя точка x_B∈D₀ (Для задач невыпуклого программирования это принципиальное требование, которое должно быть обязательно выполнено.)

Применение рассмотренного ранее метода опорной гиперплоскости в случае невыпуклой допустимой области D может привести к решению, которое значительно отличается от точки истинного минимума x* задачи (7.97). В качестве примера рассмотрим задачу невыпуклого программирования:

min x₂ при условии, что — 1 ≤ x₁ 2; (7.98)
x₂ ≤ 4; g_i (х) ≥ 0,

которая имеет локальный минимум в точке х₁* = (—0,33; 1,4) и глобальный минимум в точке x₂* = (2; —1). Применение алгоритма для решения задачи (7.98), как видно из рис. 7.7, позволяет получить только точку локального минимума х₁*.

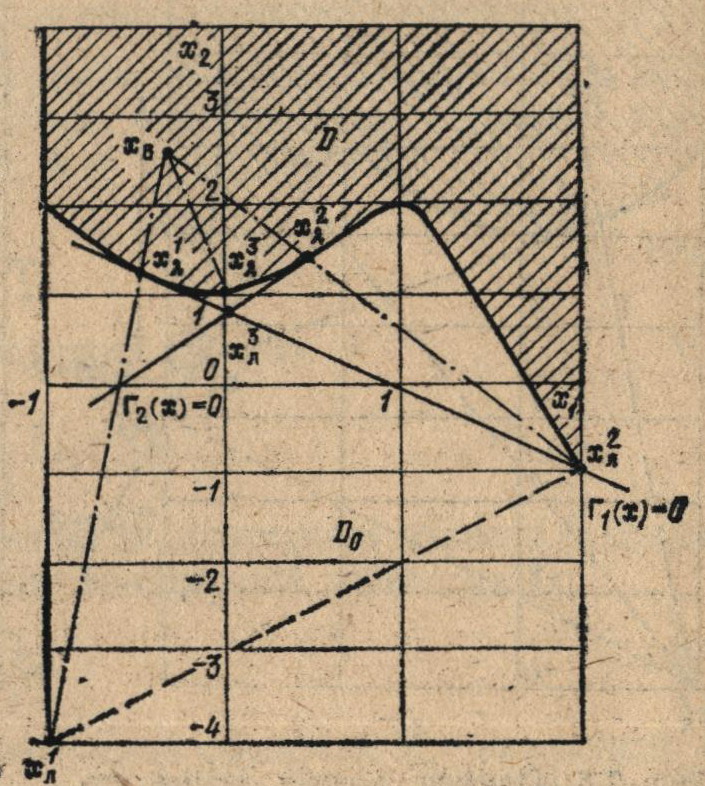
Рис.7.7. Поиск точки минимума в невыпуклой области D при помощи метода опорной гиперплоскости

Во-первых, при образовании области D₁ r для задачи линейного программирования, решаемой на r-м шаге, применяется следующее дополнительное правило. Если касательная плоскость Г_r(х) = 0 пересекает границу допустимой области D в нескольких точках, то отсекающая плоскость Г_r (х) ≥ 0 на следующем шаге не включается в систему ограничений, а задача линейного программирования решается в области D_rr = D₀. В качестве новой внутренней точки выбирается точка x_B^k ∈ D, полученная из наиболее удаленной от х_λ^r точки х_K^r (пересечения касательной плоскости Г_r (х) = 0 с границей области D) по следующей формуле:

х_B^k = х_r^K + (0, 0, …, 0, δ),

где δ — заданная положительная константа.

Задача определения числа точек пересечения касательной плоскости Г_r (х) = 0 с границей области D является одномерной задачей минимизации многоэкстремальной функции и может быть решена с помощью одного из методов глобального поиска, рассмотренного ранее. Если граница области D имеет с гиперплоскостью Г_r (х) = 0 единственную точку пересечения в х_α^r то касательная плоскость применяется как отсекающая плоскость, а задача линейного программирования решается в области D_r+1 = D_r∩Г_r(х) ≥ 0, т. е. в многограннике D, без той его части, где Г_r (х) < 0, На рис.7.8 приведен пример, иллюстрирующий использование рассмотренного правила (первого дополнительного правила) при поиске точки минимума х* с помощью алгоритма в невыпуклой области D. [ads1]

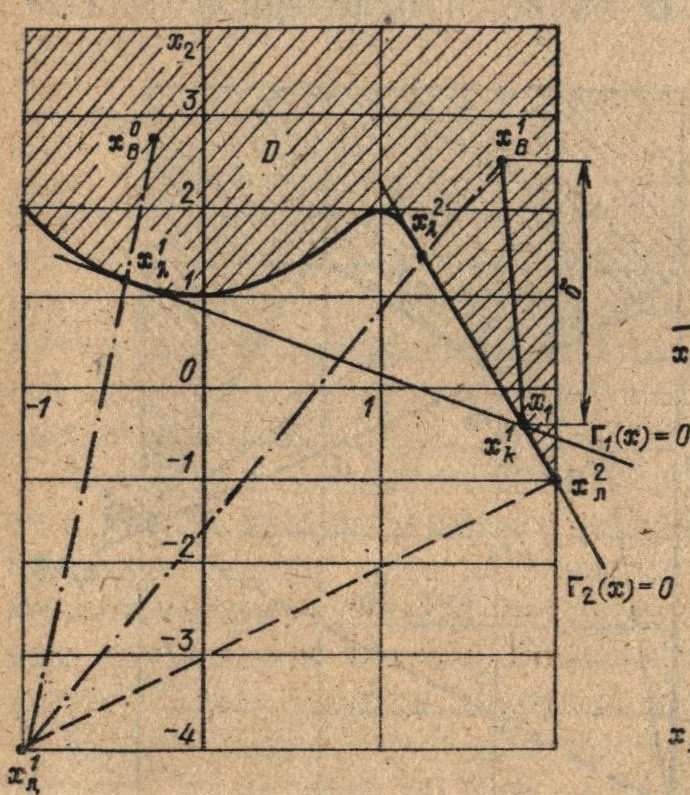
Рис. 7.8. Пример поиска точки минимума X* в невыпуклой области, иллюстрирующий использование первого дополнительного правила

Во-вторых, для заданной внутренней точки х_B⁰ ∈ D модифицированный метод опорной гиперплоскости должен не просто сходиться к расположенному рядом с точкой х_B⁰ локальному минимуму, а на каждой итерации пытаться выйти из зоны его притяжения, чтобы попасть в зону следующего более глубокого минимума. С этой целью проверяется, принадлежит ли точка x_Л^r, (оптимальное решение задачи линейного программирования, полученное на r-м шаге) области D. Если нет, то поиск по эвристическому алгоритму аналогичен поиску по методу опорной гиперплоскости и ведется в области D_r+1 = D_r∩Г_r(х) ≥ 0. В противном случае, если имеется несколько пересечений отрезка х_Л^rх_α^r с границей области D, точка х_Л^r∈D считается новой внутренней точкой и относительно нее весь процесс поиска повторяется сначала. При этом все отсекающие плоскости, полученные для старой внутренней точки, из рассмотрения исключаются, и алгоритм продолжает поиск на (r + 1)-й итерации в области D_r+1 = D₀. На рис. 7.9 приведен пример, иллюстрирующий использование второго дополнительного правила для поиска точки минимума х* с помощью эвристического алгоритма в невыпуклой области D.

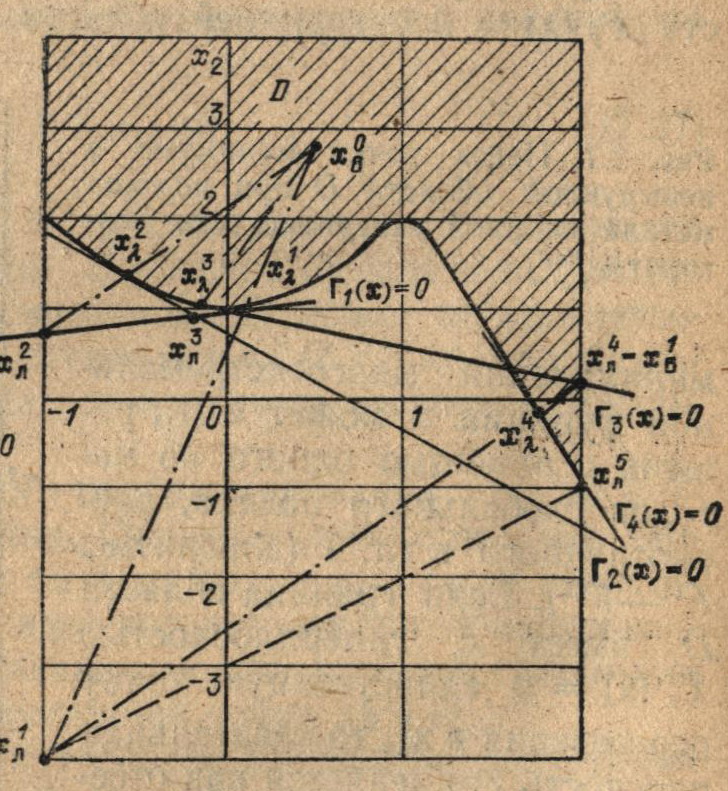
Рис. 7.9. Пример поиска точки минимума X* в невыпуклой области, иллюстрирующий использование второго дополнительного правила

Для локализации точки глобального минимума х* задачи невыпуклого программирования (7.97) необходимо многократное применение эвристического алгоритма из разных внутренних точек х_B^k ∈ D, k = 1,2, …, N, расположение которых в допустимой области D задается, например, случайным образом.

В рассмотренном алгоритме имеются процедуры, которые не нужны при решении задач выпуклого программирования. Поэтому для решения последних более эффективным является метод опорной гиперплоскости. Однако при применении алгоритма не требуется доказывать выпуклость допустимой области D перед решением задачи нелинейного программирования, что делает его использование предпочтительным и в задачах поиска точки минимума х* в выпуклой области допустимых решений D.

В задачах выпуклого программирования локальный минимум одновременно является и глобальным минимумом. Однако, если предположение о выпуклости допустимой области D снять, то это утверждение будет уже несправедливо. В связи с этим рассмотрим алгоритм, в котором задаче невыпуклого программирования:
min (c^T, x), где D = {x|g_i(x) ≥ 0, i = 1,…, m} (7.99) — невыпуклое множество, ставится в соответствие задача выпуклого программирования:
min (с^T, х), где D* — выпуклое множество. (7.100)

При ЭТОМ задачи (7.99) и (7.100) считаются эквивалентными в том смысле, что оптимальное решение задачи (7.100) х* совпадает с точкой глобального минимума х* задачи (7.99). В качестве допустимой области D* можно рассматривать выпуклую оболочку множества D, которая включает в себя все точки допустимой области. В том случае, когда область D — не выпуклое или многосвязное множество, образованное системой неравенств, выпуклая оболочка D* строится в вида замкнутого выпуклого многогранника, являющегося линейной комбинацией своих крайних точек х^k, k = 1, 2, …, s:

x = ∑ρx^k для всех х∈D⊆D*, (7.101)

где вектор ρ = (ρ₁, …, ρ_s).

В дальнейшем под выпуклой оболочкой D* допустимой области D будем понимать множество всех линейных комбинаций точек из D:

D* = {x|x = ∑∑^jx^j} (7.102)

Общей методики построения выпуклой оболочки D8, связанной о задачей выпуклого программирования (7.100), пока не существует.

Поэтому рассмотрим вопрос построения множества D* в частном случае, когда невыпуклая область D является объединением конечного числа выпуклых множеств:

D = ∪D_j, (7103)

где D_j = {x|f_j (х) ≥ 0}, j = 1, 2, …, s, — выпуклые множества.

Кроме этого будем считать, что каждая область D_j задается при помощи обратимого преобразования базового выпуклого множества D₀, в качестве которого может быть выбрано любое из множеств D_j:

D_j = a_jD₀ +V_j, j = 1,2, …,s. (7.104)

Комментарии запрещены.