Численное решение алгебраических уравнений
Численные методы решения алгебраических уравнений имеют самостоятельное значение для исследования статических моделей. Уравнение вида х = f(х) называют заданным в неявной форме, если неизвестная переменная х входит в обе части уравнения, а f — функция, не содержащая интегрирования, дифференцирования или запаздывания х.
Если решение уравнения х =f(x) существует и находится в области вещественных чисел, то оно может быть найдено по простой итерационной формуле
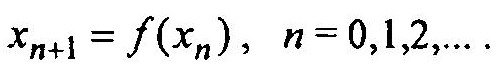
Эта формула приводит либо к сходящемуся итерационному процессу и тогда |xn+1 – xn| : xn при возрастании n будет сколь угодно малым, либо к расходящемуся итерационному процессу. Используя алгебраические преобразования, алгебраические уравнения, записанные в произвольной форме, можно представить в канонической форме:
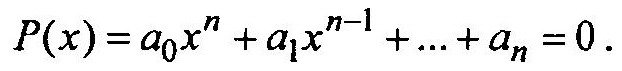
При имитационном моделировании и проектировании часто приходится решать системы линейных и нелинейных алгебраических уравнений.
Система линейных алгебраических уравнений имеет вид:
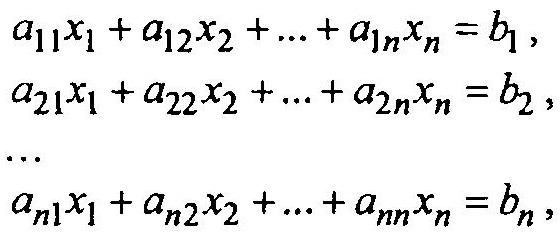
где аij и bi являются константами.
Это же уравнение в матричной форме имеет
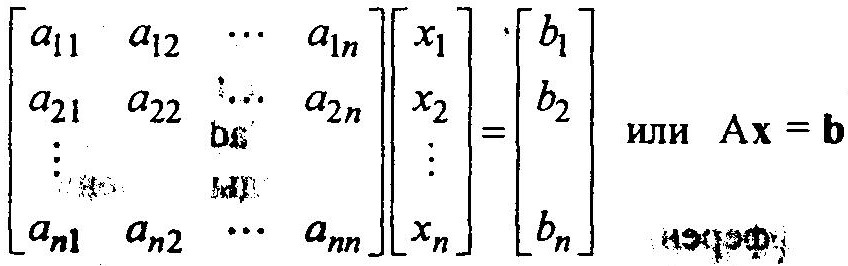
где А — матрица коэффициентов aij размерности (nхn); b — вектор столбец коэффициентов b1,b2,…,bn размерности (n x 1); х — вектор неизвестных переменных размерности (n x 1).
Матрицы бывают квадратными (размерность nxn); диагональными, в том числе единичными, симметричными (А = АТ, aij = aji); треугольными, невырожденными и вырожденными.
Распространенным методом решения системы линейных алгебраических уравнений является метод Гаусса.
Решение системы нелинейных алгебраических уравнений представляет собой более сложную задачу.
В общем случае система нелинейных алгебраических уравнений имеет вид
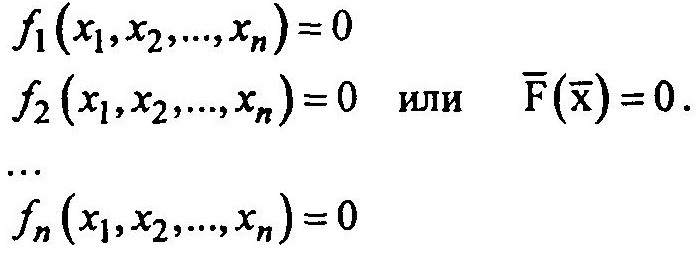
Найти точное решение системы, т.е. вектор x = (x1,x2,…,xn)T
практически невозможно. Приближенное решение получают посредством итераций различными модификациями метода Ньютона с использованием матрицы Якоби:
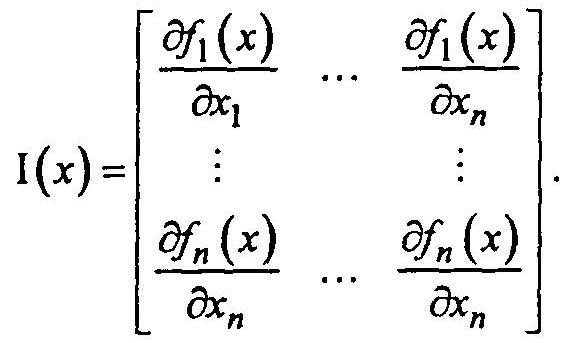
Разработаны программные средства, реализующие методы решения алгебраических уравнений. Самым популярным пакетом из известных математических программ является MathCad фирмы Math Soft Inc. В этом пакете программ реализованы методы решения систем алгебраических и дифференциальных уравнений.