Если в допустимой области D изменения управляемых параметров имеется только одно значение вектора х, то проблемы принятия решения не возникает. В тех же случаях, когда работоспособный вариант проектируемого устройства не единственен, для сравнения нескольких вариантов и выбора среди них наилучшего (в некотором смысле) необходимо ввести критерий оптимальности (функцию цели, критерий эффективности) Q (х), экстремальное значение (максимум или минимум) которого численным образом характеризует свойство одного из наиболее важных технико-экономических показателей проектируемого устройства.

Этот критерий, показывающий относительное предпочтение одного варианта по отношению к другим, определяет цель проектирования и вместе со списком управляемых параметров х и описанием допустимой области D образует математическую модель принятия решений в задаче оптимального проектирования:

min Q(x). (1.24)

Выражение (1.24) является сокращенной записью следующей обобщенной модели принятия оптимального решения:
найти значения управляемых параметров х = (x₁, х₂, …, х_n), обеспечивающих минимальное значение критерия оптимальности

Q = Q (x₁, х₂, …, х_n), (1.25)

при выполнении условий работоспособности проектируемого устройства

g_i (x₁, х₂, …, х_n) ≥ 0, i = 1, 2, …, n; (1.26)
x_j^— ≤ x_j ≤ x_j⁺, j = 1, 2, …, n. (1.27)

Таким образом, решение задачи оптимального проектирования сводится к выбору управляемых параметров х, принадлежащих допустимой области D и обеспечивающих экстремальное значение критерия оптимальности Q (х). В дальнейшем задачу (1.25)—(1.27) будем называть задачей параметрической оптимизации (задачей оптимального проектирования). Оптимальным решением этой задачи является вектор х*, удовлетворяющий системе неравенств (1.26)—(1.27) и обеспечивающий минимальное значение критерия оптимальности (1.25).

В зависимости от числа n управляемых параметров, структуры допустимой области D и вида критерия оптимальности Q (х) задача оптимального проектирования приводится к различным классам математических моделей принятия оптимального решения в рамках введенной модели (1.24).
В тех случаях, когда число управляемых параметров х больше одного (n ≥ 2), задача параметрической оптимизации называется многопараметрической задачей оптимизации, при n = 1 — одномерной задачей оптимизации. В одномерном случае осуществляется поиск минимума произвольной кривой Q (х) на некотором интервале |х^—, х⁺|:

min Q(x),

В многомерном случае решение задачи параметрической оптимизации сводится к поиску минимума функции Q (х), определенной в многомерном параллелепипеде (1 -14);

min Q(x). (1 28)

В зависимости от вида критерия оптимальности Q (х) оптимальное решение х* может быть либо точкой локального минимума, либо точкой глобального минимума.

Вектор х* называется точкой локального (относительного) минимума, если для всех точек х, принадлежащих ε-окрестности d(x*, ε) этой точки, функция Q (х) не принимает меньшего значения:

Q (х*) ≤ Q (х) для всех х∈d (х*, ε).

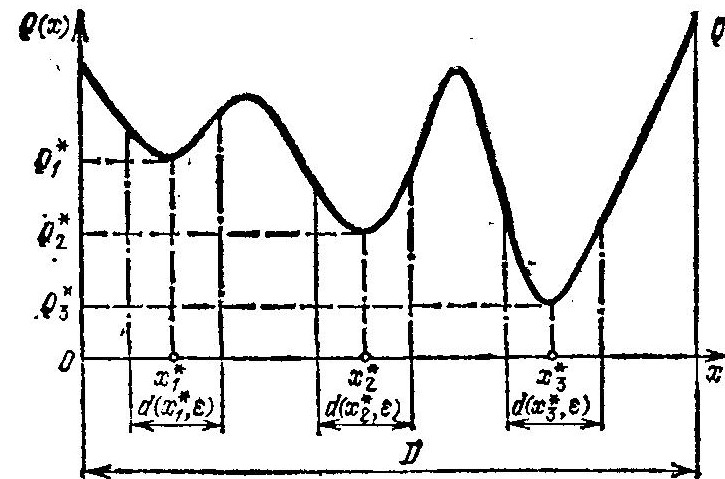
Рис. 1.6. Произвольная кривая с двумя локальными (х₁*, х₂*) и одним глобальным (х₃*) минимумом

Рис. 1.7. Одномерные унимодальные функции

Вектор х* является точкой глобального (абсолютного) минимума, если ни в одной другой точке допустимой области D функция Q(x) не принимает меньшего значения:

Q (х*) ≤ Q (х) для всех х ∈ D.

Таким образом, глобальный минимум — это наименьший из всех локальных минимумов. На рис 1.6 показаны точки локальных (х₁*, х₂*) и глобального (х₃*) минимумов для произвольной кривой Q (х).

Задача параметрической оптимизации, в которой критерии оптимальности Q (х) имеет в области D единственный локальный минимум называется одноэквтремальной (унимодальной) задачей оптимизации. Простейшими из унимолальных функций являются выпуклые функции (рис 1.7, а). Геометрически свойство выпуклости означает, что функция Q (х) расположена ниже любой прямой, соединяющей две точки на ее поверхности:

Q (αx¹ + (1 — α) x²) ≤ αQ (x¹) + (1 — α) Q (х²) для любых x¹, x¹∈D и 0 ≤ α ≤ 1.

На рис. 1.7 приведены примеры унимодальных одномерных функций.

Задача параметрической оптимизации, в которой критерий оптимальности Q (х) имеет несколько локальных минимумов, называется многоэкстремальной задачей оптимизации.

При отсутствии ограничений на параметры х и характеристики φ_i (х) задача параметрической оптимизации сводится к поиску минимума функции Q (х), определенной в n-мерном евклидовом пространстве:

min Q(x). (1.29)

Задача (1.29) называется задачей оптимизации без ограничений (задачей безусловной минимизации).

При наличии нелинейных ограничений, связывающих управляемые параметры х между собой, задача параметрической оптимизации называется задачей нелинейного программирования (задачей поиска минимума при наличии ограничений):

min Q(x), (1.30)
где D = {x|g_i (x) ≥ 0, i = 1. 2, …. m}.

В некоторых случаях задачу (1.30) можно свести к задаче безусловной минимизации вида:

min Q*(z), (1.31)

где Q*(z) = Q (х) = Q (f₁ (z), f₂ (z), …, f_n (z)); x_i = f_i (z_i) — функция преобразования i-й переменной (в частном случае функция преобразования f_i(z) может иметь вид: x_i =f_i (z_i)); z — вектор новых варьируемых переменных, компоненты которого удовлетворяют условию: -∞ ≤ z_i ≤ ∞, j = 1, 2,…, s ≤ n. (Число новых переменных z_i равно s = (n — k), где n — общее число управляемых параметров х, a k — число ограничений типа равенств.) Для того чтобы оптимальное решение z* задачи (1.31) было эквивалентно оптимальному решению х* исходной задачи (1.30), необходимо, чтобы функции преобразования удовлетворяли следующим двум условиям:

для каждого х ∈ D существует по крайней мере один действительный вектор z такой, что x_i = f_i (z), i = 1, 2,…, n;

для любых действительных чисел -∞ ≤ z_i ≤ ∞, i=1,2, …s, вектор х = (f₁ (z), f₂ (z), …, f_n (z)) принадлежит множеству D.

Задача параметрической оптимизации с ограничениями типа линейных неравенств
min Q(x), где D_x = {x|x_j^— ≤ x_j ≤ x_j⁺, j = 1, 2,…, n}, сводится к задаче безусловной оптимизации (1.31) при помощи функций преобразования вида:

x_j = x_j^— + (x_j⁺ — x_j^—) sin² z_j = 1, 2,…, n.

Комментарии запрещены.