Поскольку основой систем моделирования являются математические модели, рассмотрим конкретные формы математического описания компонент системы различными математическими формализмами.

Для адекватного представления современных систем приходится включать в их описание формализмы, описывающие, различные по своей природе физические процессы. А также их взаимное влияние друг на друга, введение деталей в описание модели можно осуществить не только за счет увеличения размерности модели, но и за счет перехода к другой математической форме ее описания.

В общем случае процесс функционирования объекта можно записать в виде

y(t) = F(u,v,v), (1.1)

где и — вектор входных воздействий; v — вектор возмущающих воздействий; х — вектор внутренних параметров; у — вектор выходных параметров, F — оператор связи, характеризующий функционирование объекта.

Оператор связи F может быть задан в виде функции, функционала, логических условий, в табличной форме и т.п. Математические модели такого вида называют динамическими, так как они описывают поведение системы во времени.

Статическая модель может быть записана следующим образом:
y = F(u,v,x).

В зависимости от характера воздействий и изменения внутренних параметров модели могут быть детерминированными и стохастическими, а в зависимости от связей между переменными — линейными и нелинейными.

Типовые математические модели позволяют упростить и сделать наглядными описания объектов. Типовые математические модели можно классифицировать, например, в зависимости от характера изменения времени и состояния (табл. 1.1).

Таблица 1.1

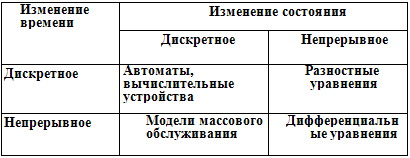
Приведенные четыре типа моделей конкретной формализации не охватывают все многообразие моделей. Но такая классификация моделей положена в основу создания большинства систем моделирования, в основу создания языков имитации. Множество объектов можно разделить на два крупных класса: непрерывные и дискретные

Основным математическим аппаратом для описания и исследования непрерывных систем служит аппарат дифференциальных уравнений. В соответствующей литературе рассмотрены дискретные системы, последовательная смена состояния которых происходит в дискретные моменты времени. Каждая смена состояний связана с изменением параметров системы, связей между ее компонентами, с изменением алгоритма работы и т.п. В интервалах между моментами смены состояний указанные выше изменения не происходят. Такие дискретные системы относятся к системам передачи и обработки данных, и они описываются моделями массового обслуживания.

Многие современные системы совмещают в себе дискретные и непрерывные процессы. Такие системы относят к комбинированным, непрерывно-дискретным системам.

Разработка систем управления является одной из наиболее интересных областей применения идей и методов моделирования, так как здесь сочетаются как исследовательские, так и проектные приложения моделирования. Всякая система управления состоит из объекта управления и управляющей части. В процессе разработки решается исследовательская задача — получение описания объекта управления и исследование его свойств и проектная задача — синтез управляющей системы для данного объекта.

Комментарии запрещены.