Матричное представление факторного планирования эксперимента
Выражения для вычисления b0 и b1, получаются громоздкими, а при большем числе факторов задача вычисления коэффициентов еще больше усложняется.
В связи с этим используют матричную форму записи уравнений и решений относительно коэффициентов b. Если было проведено N опытов, в каждом из которых задавалось определенное сочетание факторов (в n-м опыте — х0u, х1u,….,хmu), то все возможные сочетания факторов можно представить матрицей X, все результаты — матрицей Y, а все искомые коэффициенты — матрицей В:
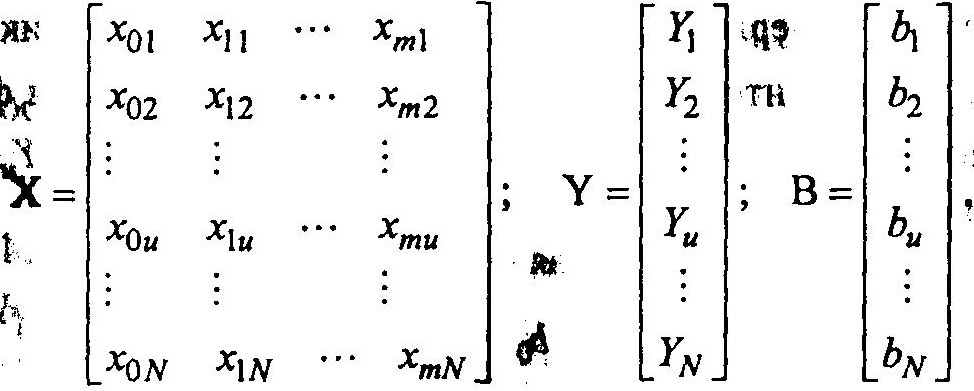
В результате получим уравнение в матричной форме
Y = XB (1)
решение можно получить в виде
B = X-1Y.
В такой форме надо обращать матрицу, что непросто.
Чтобы упростить решение, запишем (1) в эквивалентной форме
ХТY = ХТXВ,
где XТ — транспонированная матрица X. Тогда получаем
СВ = ХТY, (2)
где матрица С = XТX — квадратная и имеет (1 + m) строк и столбцов.
Для определения коэффициентов А, умножим на матрицу С-1 слева обе части уравнения (2). Поскольку С-1С есть единичная матрица, то получаем:
B = C-1XTY (3)
Анализ матрицы С показывает, что она симметричная: на главной диагонали элементы имеют вид 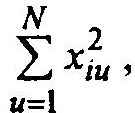 , а элементы, симметрично расположенные сверху и снизу от главной диагонали, равны между собой, т.е.
, а элементы, симметрично расположенные сверху и снизу от главной диагонали, равны между собой, т.е.
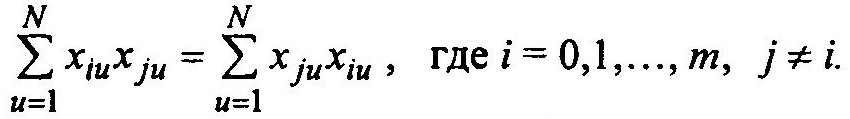
Для получения обратной матрицы С-1 матрица С должна быть невырожденной, т.е. её определитель не должен равняться нулю
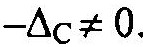
Если точность аппроксимации не достигается, то надо изменить полином.
Любое изменение полинома приведет к изменению всех коэффициентов bi. Стало быть снова надо обращать матрицу C, что приводит к существенному росту объема вычислений. Другими словами, при изложенной процедуре все коэффициенты оказываются зависимыми друг от друга. Конечно, хотелось бы избежать этих трудностей и чтобы коэффициенты, вычисленные при исходной, начальной модели, не надо было бы пересчитывать при усложнении модели для достижения большей точности аппроксимации. Оказывается, преодолеть указанные трудности можно с помощью выбора сочетания факторов в каждом опыте по специальному алгоритму. Вычислительные трудности существенно уменьшаются, если матрица С является диагональной. Тогда обратная матрица находится очень просто
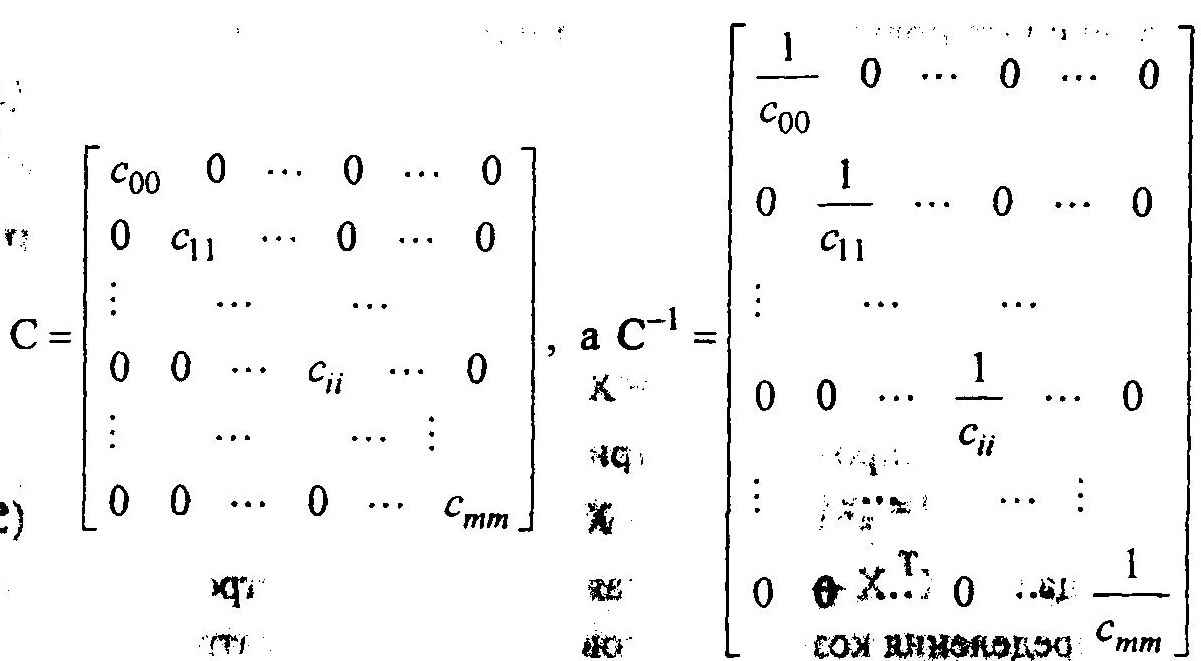
В этом случае получим 1 + m – независимых уравнений в соответствии с уравнением (5.10)
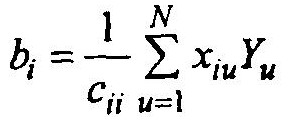
И с учетом того, что
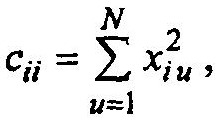
Имеем в итоге:
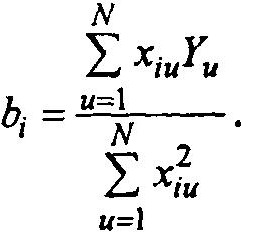
Итак, необходимо добиться, чтобы матрица С удовлетворяла условию cij = cji = 0 (элементы над и под главной диагональю) или что тоже
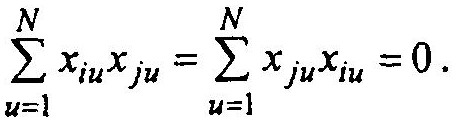 (4)
(4)Следовательно, условие (4) означает равенство нулю произведения любых двух столбцов матрицы X. Но столбец матрицы можно рассматривать как вектор. Если скалярное произведение двух векторов равно нулю, то векторы ортогональны. Поэтому условие (4) называют условием ортогональности матрицы X, а соответствующий выбор плана эксперимента — ортогональным планированием.