Образовательный блог – всё для учебы

Рассмотренные в полном факторном эксперименте примеры свидетельствуют о том, что ПФЭ полностью определяют коэффициенты для линейного уравнения

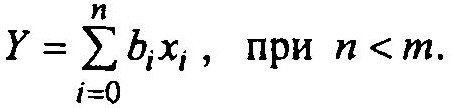
В такой модели необходимо определить n + 1 искомых коэффициентов. Как построить экономно эксперимент? В этом случае строят план эксперимента, который представляет часть плана ПФЭ. Такие планы называют дробными репликами ПФЭ или дробным факторным экспериментом (ДФЭ). Но при этом все требования к столбцам матрицы планирования должны соблюдаться, т.е.

План дробного факторного эксперимента строится очень просто. Так, для линейной модели из трех факторов требуется ДФЭ 2^3-1, содержащий четыре опыта. Таким образом, строится план эксперимента для меньшего числа факторов (3-1 = 2), а оставшиеся факторы варьируются как произведения каких-либо факторов, включенных в первую группу. Но, если есть уверенность, что в выбранном интервале варьирования факторов объект может быть оценен линейной моделью, то смешанные коэффициенты b₁₂, b₁₃, …. стремятся к нулю. С учетом сказанного построим ДФЭ 2^3-1. В этом случае факторами х₁ и x₂ варьируют как при ПФЭ, а вместо произведения x₁x₂ (b₁₂= 0) вводят дополнительный фактор х₃. Другими словами укороченную матрицу планирования строим для трех факторов и дополнительный фактор х₃ будет меняться как произведение x₁x₂.

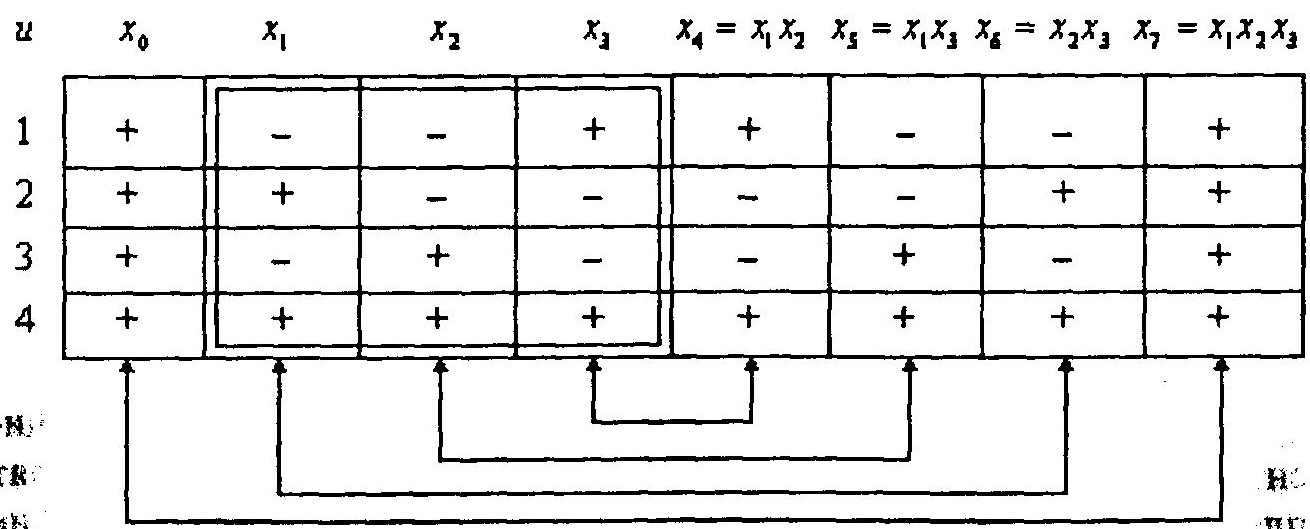
Матрица планирования ДФЭ 23-1 приведена на рисунке ниже.
В матрице планирования четыре пары одинаковых столбцов, а это значит, что соответствующие коэффициенты неразличимы и можно судить лишь об их совместной величине (смешанные оценки коэффициентов) — линейные эффекты смешиваются с эффектами взаимодействия. Но, если объект линейный, b_ij и b_ijk равны нулю. Тогда
из четырех опытов найдем истинные значения b₀ и b_i (b₁,b₂,b₃)

Если объект не является линейным и поверхность отклика, найденная по уравнению, отличается сильно от действительной, то надо ставить ПФЭ.
Дробные реплики особенно удобны при большом числе факторов (n ≥ 5), так как при этом коэффициенты при факторах b₁ — b_n смешиваются при тройных и более высоких взаимодействиях, влияние которых существенно слабее, чем при двойных взаимодействиях. Поэтому влиянием этих взаимодействий можно пренебречь.

Общий вывод: планы ПФЭ 2ⁿ или ДФЭ 2^n-k позволяют получить решение для линейных и неполных квадратичных полиномов (без квадратичных членов). Невозможность использования этих планов можно считать, например, расхождение между истинным значением Y_n и У, предсказанным аппроксимирующим выражением в нулевой точке плана (x₁=x₂=x_n=…= 0), превышающее допустимое. Более точную аппроксимацию можно получить разными способами. Распространение получил переход к планам второго порядка, позволяющим найти коэффициенты при квадратичных членах аппроксимирующего
полинома (x_i²).

1. Полный факторный эксперимент
2. Ортогональное центральное композиционное планирование
3. Регрессионная модель проектирования
4. Регрессионный анализ факторного планирования
5. Основы факторного планирования эксперимента
6. Матричное представление факторного планирования эксперимента
7. Общий подход к статистическому моделированию
8. Введение в понятие моделирования
9. Модели в пространстве состояний
10. Z – преобразование
11. Настройки синтаксиса SQL
12. Экспериментальный подход к получению модели объекта
13. В мировом парке ЭВМ
14. Реализация имитационного моделирования
15. Корреляционный метод идентификации
16. Назначение встроенного SQL
17. Численные методы интегрирования