До сих пор, рассматривая вопросы планирования эксперимента, исходим из того, что величина Y не изменялась при повторении одного и того же опыта, возможно ли это? Да, возможно. Например, при построении моделей и анализе вычислительных устройств, электромеханических устройств нередко встречается ситуация, когда опыты дают точные результаты. Поэтому рассмотренный подход представляет практический интерес. Но во многих реальных задачах при проведении экспериментов Y будет принимать различные значения появляются ошибки опыта. Эти ошибки обусловлены случайными, неучитываемыми в опытах факторами различного происхождения (внешние возмущающие воздействия, шумы, изменения параметров).

В этих условиях Y — случайная величина и анализ требует применения теории вероятностей и математической статистики.

В общем случае нельзя ограничиваться одним опытом — каждый опыт надо повторять несколько раз. В этих условиях рассмотренные, полиноминальные уравнения становятся уравнениями регрессии.

Регрессия — зависимость среднего значения какой-либо величины от одной или нескольких других величин.

Регрессионная модель является моделью в стационарном режиме.

Уравнение регрессии позволяет оценить наиболее вероятное расположение поверхности отклика. При регрессионном анализе планы эксперимента строят так, чтобы при минимальном числе опытов коэффициенты уравнения регрессии определялись с наименьшими возможными дисперсиями.

Регрессионный анализ, как всякий статистический метод, применим при определенных постулатах, предпосылках.
1. Результаты наблюдений функции отклика Y₁, Y₂, Y_N в точках факторного пространства есть случайная величина с нормальным законом распределения.

В этом случае Y полностью характеризуется двумя величинами — математическим ожиданием и дисперсией.

Оценку математического ожидания случайной величины и значение дисперсии можно получить посредством К повторений одного опыта:

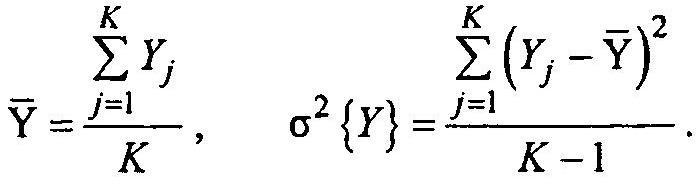
При оценке α²{V} в знаменателе (К-1), так как из общего числа К-опытов данные одного опыта были использованы для вычисления Y(-).
Чаще всего число опытов в каждой точке плана К =2 — 4. В результате получится N средних значений (Y^—₁, Y^—₂,…, Y^—_n ).

Средними значениями отклика заполняют соответствующий столбец в матрице планирования и вычисляют коэффициенты b_i точно так же, как это делалось ранее.

2. Дисперсия Y не зависит от абсолютной величины Y. Это требование проверяется с помощью критерия однородности дисперсии в разных точках фазового пространства.

Нарушение этой предпосылки недопустимо. Требование однородности дисперсии используется для того, чтобы иметь право пользоваться средним значением Y для определения коэффициентов b_i полинома.

Дисперсии в опытах однородны, если они не зависят от того, в какой точке фазового пространства проводится опыт. Из этого не следует, что все N дисперсий должны быть равны — достаточно лишь отсутствия значимого различия между ними, что проверяется, например, статистическим критерием Фишера, предназначенным для сравнения двух дисперсий. Критерий Фишера (F-критерий) представляет собой отношение большей дисперсии к меньшей. Полученная величина сравнивается с табличной величиной F-критерия (эти таблицы приводятся в книгах по прикладной статистике). Дисперсии однородны, если экспериментальное значение критерия Фишера не превышает табличного.

3. Значения факторов — неслучайные величины, т.е. факторы можно устанавливать на заданном уровне существенно точнее, чем разброс в значениях Y_i.

4. Факторы не коррелированы, т.е. их можно устанавливать независимо друг от друга.

Отметим еще следующее. Гипотезу о нормальном распределении Y при сомнении в этом можно проверить с помощью стандартного статистического теста с применением x² -критерия (критерия Пирсона).

Итак, в условиях шумов, помех, в стохастических условиях определение коэффициентов b_j аппроксимирующего полинома методом факторного эксперимента состоит из следующих этапов:
1) составление плана эксперимента;
2) проведение эксперимента с повторением каждого опыта К раз;
3) проверка однородности дисперсии;
4) вычисление коэффициентов b_i, с проверкой их статистической значимости;
5) получение аппроксимирующего полинома со значимыми коэффициентами b_i,
6) проверка адекватности поверхности отклика.
Если какой-либо коэффициент окажется статистически незначимым, т.е. b_i = 0, то им пренебрегают.

Чтобы проверить гипотезу об адекватности представления результатов эксперимента, найденным уравнением регрессии достаточно оценить отклонение предсказанной уравнением регрессии функции отклика от экспериментальных значений функции отклика в тех же точках факторного пространства.

Таким образом, получение регрессионной модели при планировании машинных экспериментов требует введения в модель эквивалентной помехи, шумового эффекта и других воздействий, имеющих стохастическую природу.

Комментарии запрещены.