Основы факторного планирования эксперимента
Поскольку при проведении натурных и машинных экспериментов широкое распространение получила теория и методы планирования эксперимента (как ветвь математической статистики), в данной главе приведены краткие сведения по основам планирования эксперимента и регрессионному анализу на основе аппарата факторного планирования эксперимента.
Более полное и обстоятельное изложение теории планирования эксперимента читатель может найти в соответствующей литературе. Здесь же рассмотрим использование этого аппарата для получения и анализа статических моделей, моделей в установившихся режимах.
Математическая теория планирования эксперимента позволяет повысить эффективность экспериментальных исследований. Основы этой теории заложил английский статистик Р. Фишер. Он впервые показал целесообразность одновременного варьирования многими переменными в противовес широко распространённому однофакторному эксперименту.
Планирование эксперимента — это процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи.
При этом существенно следующее:
1) одновременное варьирование всеми переменными, определяющими изучаемый процесс, по специальным правилам, алгоритмам;
2) стремление к минимизации общего числа опытов.
В данном случае используется кибернетическое представление о модели объекта в виде «черного ящика». Пусть в процессе исследования какого-либо объекта («черного ящика») некоторое качество его или целевая функция Y зависит от нескольких величин
x1, x2, …, xn
т.е.
Y = F{x1, x2, …, xn} (1)
Переменные хi представляющие варьируемые переменные, называют факторами, а Y — выход, функция отклика, целевая функция. Выходов Y может быть несколько.
В планировании могут участвовать только независимые факторы, которые можно устанавливать и поддерживать на фиксированных уровнях в течение опыта.
При этом каждый фактор xi может принимать в опыте одно из нескольких допустимых значений. Эти значения называют уровнями, фиксированный набор уровней факторов определяет одно из возможных состояний объекта и один опыт в эксперименте. Все возможные наборы уровней факторов определяет общее число возможных различных опытов.
В качестве модели рассматривается представление (1) в виде степенного ряда
 (2)
(2)На практике ограничиваются конечным числом членов разложения, т.е. неизвестная функция аппроксимируется усеченным полиномом некоторой степени.
Каждый фактор имеет свой допустимый диапазон изменения, т.е. известны граничные значения Ximin , Ximax .
Каждому фактору соответствует своя координатная ось, а образованное таким образом пространство называют факторным пространством.
Назначая граничные значения, задаем область определения функции Y в факторном пространстве. На рисунке представлена область экспериментирования функции двух переменных.
Поскольку факторы в общем случае размерные величины, их кодируют, чтобы иметь дело с безразмерными факторами. Операция кодирования представляет собой линейное преобразование факторного пространства, что ведет к переносу начала координат факторного пространства в точку с координатами
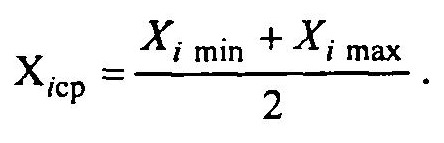
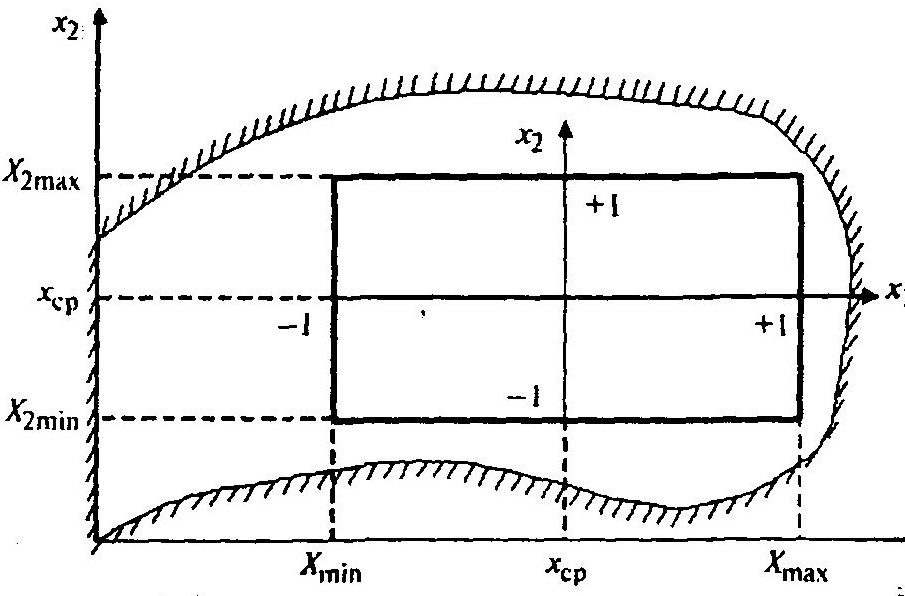
Рис. Область экспериментирования функции двух переменных
Тогда для каждого фактора Ximin будет соответствовать -1, а Хimax +1. Кодированные значения факторов хi определяются следующим соотношением:
 (2)
(2)Теперь уравнение (2) можно переписать через кодированные факторы в виде
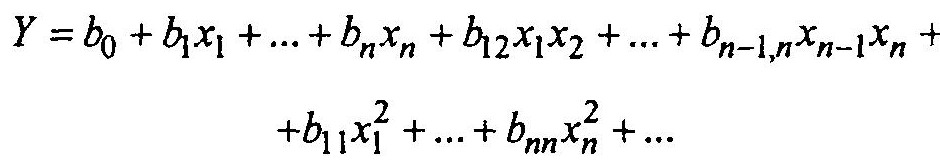 (3)
(3)или
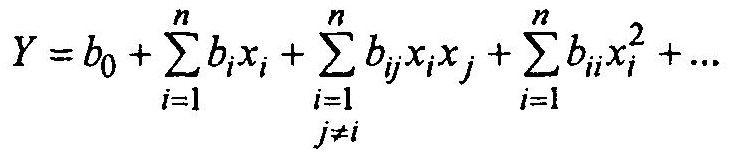 (4)
(4)Уравнение (4) можно переписать в еще более компактной форме, если ввести фиктивный фактор х0, тождественно равный единице, и обозначить все двойные, тройные взаимодействия, а также квадраты факторов символом Xi, а соответствующие коэффициенты символом bi
 (5)
(5)Пример. Пусть имеем два фактора Х1 и Х2. Тогда в соответствии с уравнением (4)
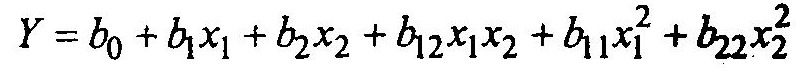
или с в соответствии (5.5)
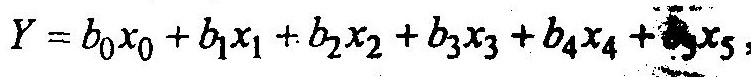
и т.д.
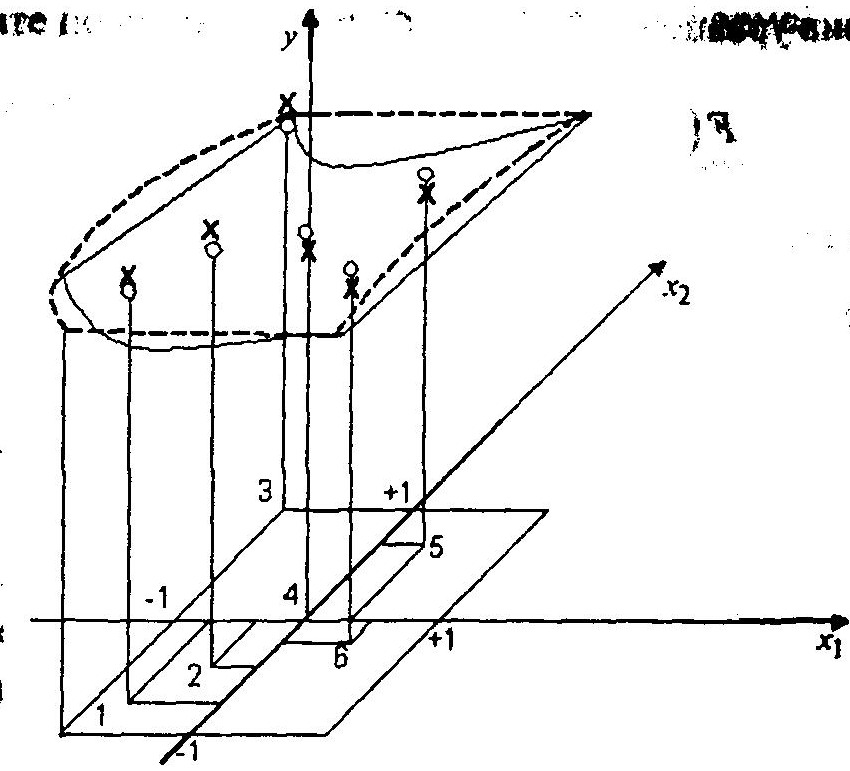
Рис. 2. Поверхность отклика в двухфакторном пространстве
В соответствии с (5) задача нахождения Y заключается в том, чтобы на основе эксперимента при вариации xi определить неизвестные коэффициенты bi.
Выражения (1) и (5) называют функцией отклика, представляющую в факторном пространстве в общем случае поверхность отклика. На рис. 2 показана поверхность отклика в двухфакторном пространстве.
Близость аппроксимирующей поверхности к истинной можно оценить тем или иным критерием. В качестве такой меры близости удобно выбрать квадратичную форму вида
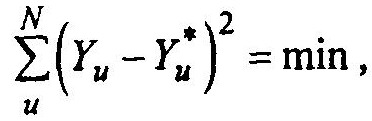 (6)
(6)где N — число экспериментальных значений функции отклика, число опытов в эксперименте; и — номер опыта; Y — значения функций отклика, предсказанная аппроксимирующим выражением; Yu — значения истинной поверхности отклика.
Рассмотрим пример для случая одного фактора:
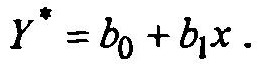 (7)
(7)Подставив уравнение (5.7) в (5.6), получим:
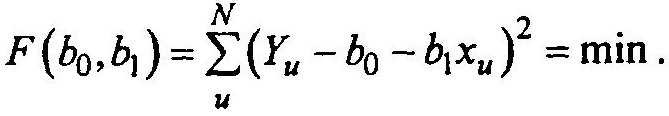
Чтобы найти экстремум, приравняем нулю частные производные:
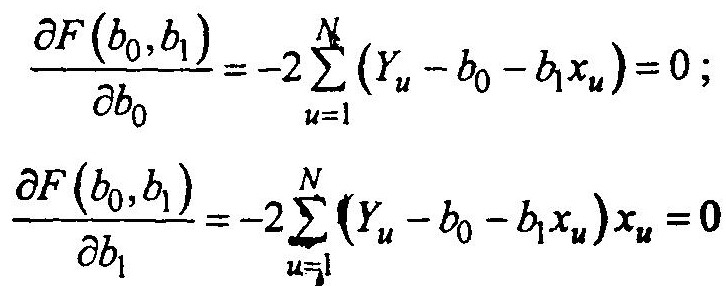
или
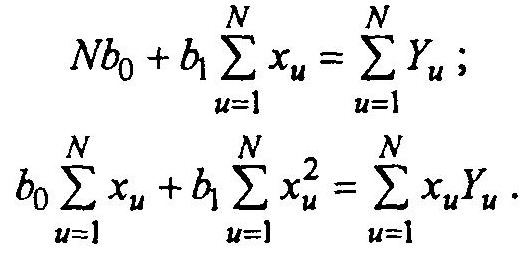
Решая эту систему, получаем искомые значения b0 и b1