Рассмотрим суть корреляционного метода идентификации. Работы Винера и Колмогорова показали, что лучшая математическая модель, удовлетворяющая критерию минимума среднеквадратической ошибки между выходом модели и выходом реального объекта, получается, если динамическая характеристика в виде весовой функции w(t) удовлетворяет уравнению вида:

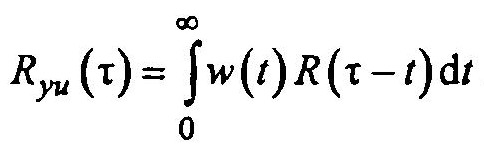
Решение уравнения относительно искомой w(t) связано с
большим объемом вычислений, что требует применения ЭВМ. Метод назван корреляционным, так как в основе его — вычисление оценок корреляционных функций.

Пассивный корреляционный метод идентификации представлен схемой на рисунке ниже.

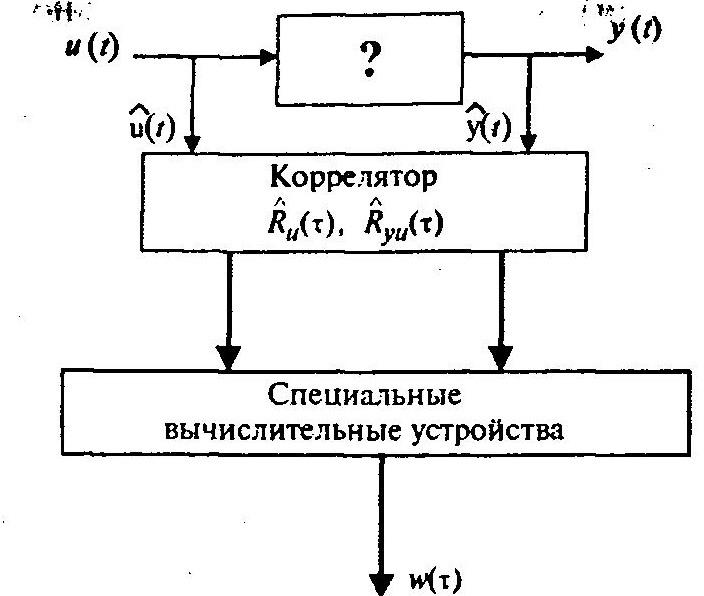
Рассмотрим решение этой задачи. Из-за ограниченной длительности реализаций входа u(t) и выхода y(t) (конечное время наблюдения) имеем дело лишь с оценками соответствующих корреляционных
функций R^_u(t) и R^_yu(t).

Где Т_н – конечное время наблюдения.

Как выбрать Т_н? Для реальных объектов при t > Т_п.п. (длительность переходного процесса) w(t) = 0.

Время переходного процесса можно оценить соотношением Т_п.п = (3 — 5) Т_max, где Т_max — максимальная постоянная времени, которая характеризует объект. Кроме того, примем во внимание, что при времени корреляции τ > τ_max R_u(t) = 0 и R_yu (t) = 0 .

В результате исходное уравнение Винера—Колмогорова можно записать в виде

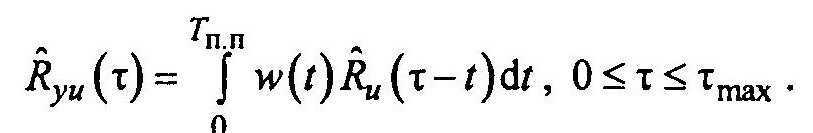
Для решения этого интегрального уравнения на ЭВМ относительно w(t) его заменяют на систему алгебраических уравнений. Для этого рассматриваем дискретные значения т посредством квантования через интервалы At, а вместо интеграла переходим к сумме. Обозначим соответственно число квантов:

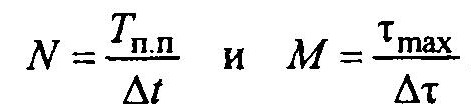
В результате от интегрального уравнения переходим к сумме:

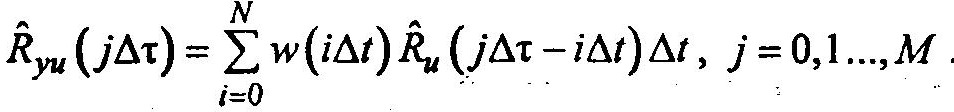
Итак, получили М+1 алгебраических уравнений. В основу критерия решения задачи относительно w закладывается «невязка» — разница между левой и правой частями уравнения. Удобно оперировать квадратом «невязки».
Решение будем искать из условия минимума функционала вида

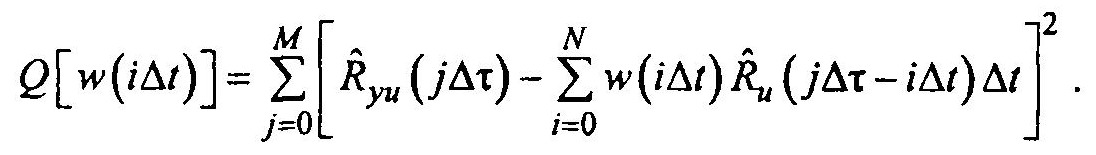
Необходимо определить такие значения w(it), при которых
квадрат «невязки» принимает минимальное значение. Условие этого минимума можно задать в виде

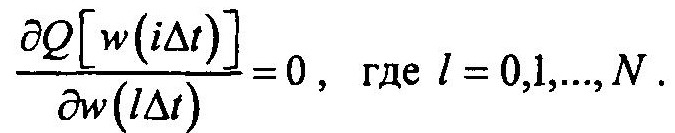
В результате алгоритм решения задачи формально завершен. Однако на практике решение подобных интегральных задач встречает трудности. Такие задачи относят к математически некорректно поставленным задачам.

Корректно поставленной задачей считается задача, о которой известно, что:
• решение существует;
• решение единственно;
• решение устойчиво к малым изменениям исходных данных.

Последнее условие означает, что с уменьшением погрешностей
исходных данных приближенные значения неизвестных, искомых в результате решения задачи, стремятся к точным.

При невыполнении хотя бы одного из приведенных условий задача считается некорректно поставленной.

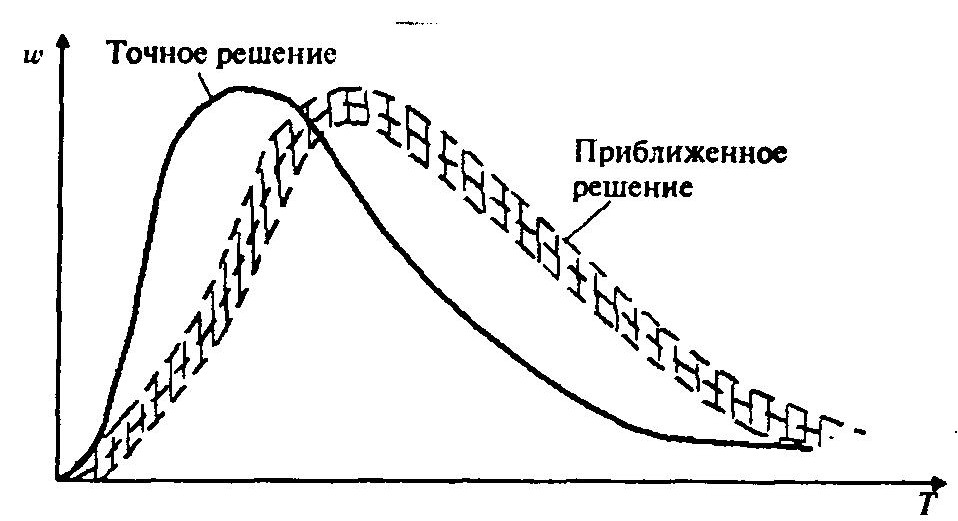
В этом случае уточнение исходных данных (до все более далеких знаков после запятой) не улучшают результаты — они будут скакать, не успокаиваясь на каком-то месте, т.е. не имеют тенденции к стабилизации (рисунок ниже).

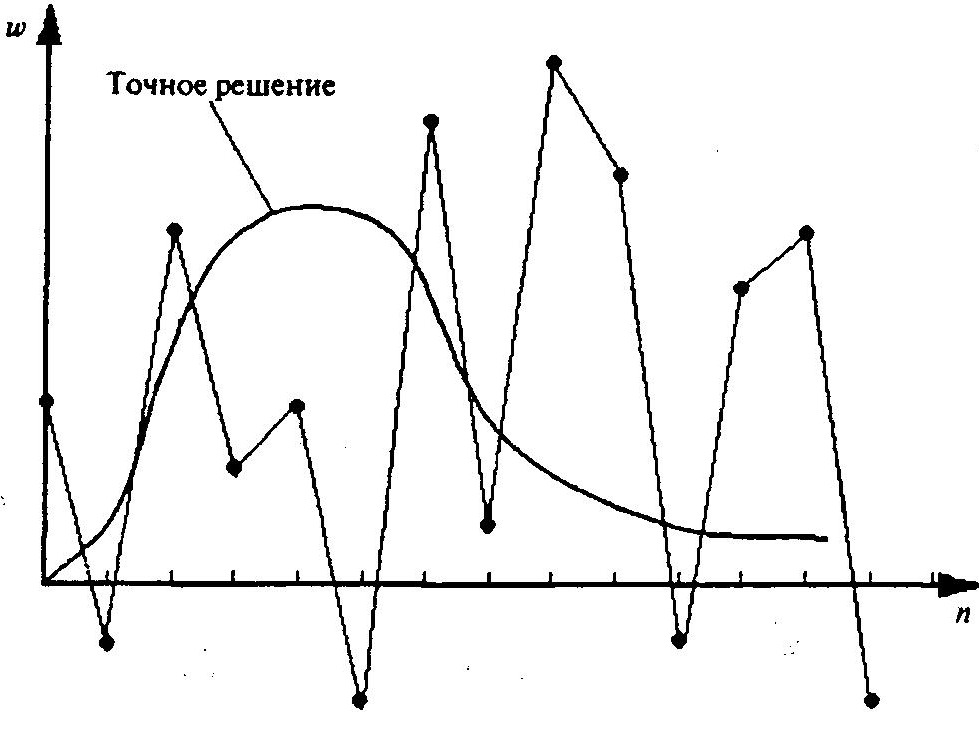
Решение дает большие разбросы, не позволяющие сделать определенные выводы, т.е. получить решение. Почему? Это результат плохой обусловленности матрицы системы алгебраических уравнений, т.е. близости к нулю определителя матрицы.

Используемые при решении оценки R^_u (т) и R^_yu (т), являясь случайными величинами, представляют собой естественный источник ошибок при задании исходных данных в уравнении. А при плохо обусловленной матрице системы малым ошибкам в задании исходных данных будут соответствовать большие разбросы в результатах решения. Подобные задачи встречаются в медицине, в геологии и других отраслях.

Следовательно, без принятия специальных мер получить математическую модель при таком подходе невозможно. Академик А.Н. Тихонов для решения таких некорректных задач предложил метод, который получил название регуляризации.

Сущность регуляризации заключается в замене точной задачи приближенной, дающей устойчивое решение.

Предлагается искать решение из условия минимума функционала вида

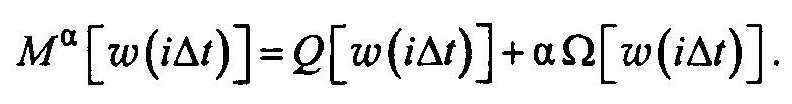
Добавка в виде ψ[w(it)] приводит как бы к сглаживанию решения относительно w(t).

В качестве регуляризирующей добавки можно выбрать

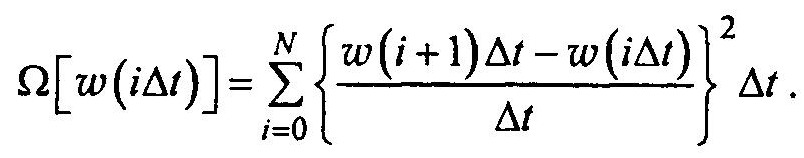
Теперь из условия минимума

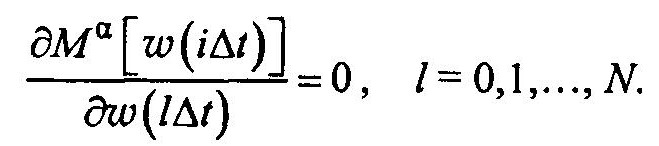
Можно получить систему линейных алгебраических уравнений, решение которой будет представлять собой ординаты искомой весовой функции w(it). Получаемое приближенное решение зависит от выбора α. Чем больше α, тем сильнее сглаживается решение, но оно будет и более смещенное.

А можно ли обойти некорректную постановку задачи идентификации? Оказывается, некорректность исчезает при активном способе идентификации.

Активный метод идентификации связан с подачей специальных тестовых сигналов на вход исследуемого объекта.

Активный эксперимент может быть реализован как в режиме нормальной работы объекта, так и при отключении объекта. В первом случае тестовый сигнал от специального источника добавляется к основному рабочему сигналу, а во втором случае — на объект подается лишь тестовый сигнал.

Схема активного метода идентификации представлена на рисунке ниже

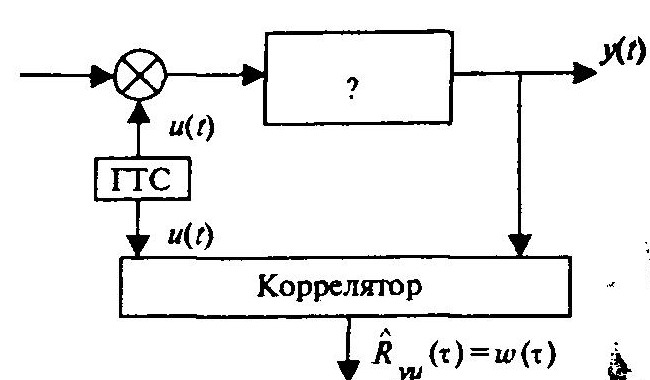
Однако не на все объекты можно подавать дополнительные возмущающие воздействия.

Представим себе, что на вход объекта подается тестовый сигнал с автокорреляционной функцией в виде 8-функции R (т) = σ(т).
Тогда решение уравнения Винера—Колмогорова принимает вид:

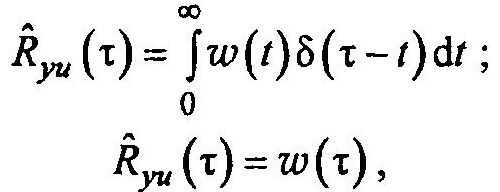
т.е. весовая функция совпадает с взаимно-корреляционной функцией. Некорректность задачи здесь не имеет места, так как вследствие свойств 5-функций нам не нужно решать систему алгебраических уравнений.

В качестве генератора тепловых сигналов (ГТС) можно использовать генератор ПСДС. Рассмотренные корреляционные методы идентификации относятся к методам идентификации в широком смысле, так как весовая функция позволяет получить как структуру, так и параметры модели. В литературе приводятся структуры моделей и соответствующие им весовые функции, что позволяет подобрать структуру для экспериментально полученной весовой функции, имеющей близкий вид.

Комментарии запрещены.