Коаксиальные цилиндры являются простейшей системой электродов, для которой уравнения (1) — (4) могут быть проинтегрированы аналитически.

div E = ρ/ε₀ (1)
E = — grad φ (2)
div J = 0 (3)
J = ρkE (4)

Принимая во внимание, что в цилиндрических координатах напряженность поля зависит только от текущего радиуса, уравнение (1) можно записать в виде:

1/r d/dr (rE) = ρ/ε₀ (5)

Обозначив через А ток коронного разряда на единицу длины электрода, уравнение неразрывности (3) можно представить в виде:

A = 2πrJ

Отсюда, используя (4), можно получить:

ρ = A/(2πrJE) (6)

После подстановки (6) в (5) последнее превращается в уравнение с разделяющимися переменными, которое легко интегрируется:

∫ rEd(rE) = A/(2πrJE) ∫rdr

Таким образом,

E = √[A/(2πrJE) (1 — r₀²/r) + (E₀r₀/r)²] (7)

При r >> r₀

E = √[A/(2πrJE) + (E₀r₀/r)²] (8)

Для интенсивного коронного разряда, когда U >> U₀ (U₀ — начальное напряжение), второе слагаемое в (8) существенно меньше первого, и, следовательно,

E = √[A/(2πrJE)] (9)

Из (8) и (9) следует, что напряженность поля в значительной части промежутка между коаксиальными цилиндрами постоянна (рис. 1).

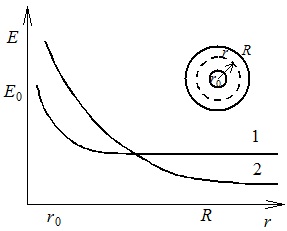
Распределение электростатического поля (1) и поля при
униполярном коронном разряде (2) между коаксиальными цилиндрами

В соответствии с (6) плотность объемного заряда изменяется по гиперболе. Различие в распределениях электростатического поля и поля при коронном разряде обусловлено действием объемного заряда, сосредоточенного в промежутке.

Для определения вольтамперной характеристики коронного разряда A = f(U) используется условие:

∫ Edr = U

При подстановке в это уравнение в уравнения (7) и его интегрирования после упрощений получается уравнение вольтамперной характеристики, которое записывается в обобщенном виде:

I = kGU(U-U₀) (10)

где G = 8πε₀ / (R²ln(R/r₀)) (1 + 2.75×10^-2√(R/r₀).

Для других систем электродов используются приближенные методы, например, метод Дейча — Попкова. Пример распределения напряженности поля при коронном разряде для системы «провод-плоскость» представлен на рис. 2.

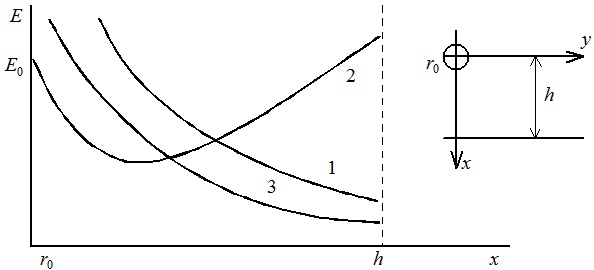
Распределение напряженности поля (1 — электрического и 2 — при коронном разряде) и плотности объемного заряда (3)

В отличии от «коаксиальных цилиндров» при коронном разряде напряженность поля возрастает по направлению к плоскости, а не остается постоянной. Такое распределение поля характерно и для других систем электродов с цилиндрическими коронирующими электродами. Вольтамперная характеристика и для других систем электродов может быть представлена в виде (10), но коэффициент G в этом случае имеет свой вид.

Комментарии запрещены.