Рассмотрим движение механической системы, имеющей n степеней свободы, на которую наложены голономные стационарные удерживающие связи. Уравнения движения системы можно записать в форме уравнений Лагранжа II рода

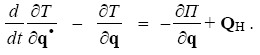(1.1)

Здесь T =1/2q^•TA(q)q^•, П = П(q) — кинетическая и потенциальная энергия системы, q = (q₁, …, q_n)^T, q^• = (q₁^•, …, q_n^•)^T — n-мерные векторы-столбцы ее обобщенных координат q_i и скоростей
q_i^•, Q_Н = Q_Н(q,q^•) = (Q_Н1, …, Q_Нn)^T — вектор-столбец обобщенных неконсервативных сил.

После дифференцирования уравнения (1.1) можно записать в виде
A(q)q^•• + b(q,q^•)+ c(q) = Q_Н(q,q^•), (1.2)
где b(q,q^•), c(q) – некоторые нелинейные вектор-функции, которые получаются после дифференцирования кинетической и потенциальной энергий.

Пусть уравнения (1.1) и, соответственно, уравнения (1.2) имеют частное решение
q_p = ξ(t), q_p^• = ξ^•(t) , (1.3)
удовлетворяющее начальным условиям
q_p(t₀) = ξ(t₀) = ξ₀, q_p^•(t₀) = ξ^•(t₀) =ξ₀^•. (1.4)
Если решение (1.3) подставить в уравнения (1.2), то получим тождество

A(ξ)ξ^•• + b(ξ,ξ^•)+ c(ξ) = Q_Н(ξ,ξ^•).
Решение (1.3) — (1.4) описывает некоторое движение системы (положение равновесия, стационарное движение, программное движение и т.д.), которое нас интересует и которое
мы хотим исследовать.

Сделаем постановку задачи об исследовании устойчивости движения (1.3) — (1.4).

Следуя А.М. Ляпунову введем следующие определения.

Определение 1.1. Движение (1.3) — (1.4) системы (1.1), устойчивость которого исследуется, называется невозмущенным движением.

Примеры невозмущенных движений: нижнее или верхнее положение маятника, движение спутника по заданной круговой орбите, вращение ротора с постоянной угловой скоростью, движение схвата манипулятора или движение мобильного робота по заданной траектории с заданной скоростью и т.д.

Для исследования устойчивости невозмущенное движение (1.3) — (1.4) необходимо сравнить с другими движениями (возмущенными) системы (1.1), которые запишем в виде
q = q (t), q^• = q^•(t), (1.5)
существующими у системы (1.1) при тех же обобщенных силах Q, но удовлетворяющими другим начальным условиям, которые можно записать в виде
q(t₀) = ξ₀+ x₁₀, q^•(t₀) = ξ₀^•+ x₂₀. (1.6)

Величины x₁₀, x₂₀ — некоторые вещественные постоянные, которые называются начальными возмущениями (их еще называют мгновенными возмущениями).

Будем считать, что начальные возмущения x₁₀, x₂₀ численно достаточно малы.

Определение 1.2. Движения (1.5) — (1.6) системы (1.1), с которыми сравнивается невозмущенное движение, называются возмущенными движениями.

Возмущенное движение полностью определяется постоянными величинами начальных возмущений x₁₀, x₂₀, поскольку действующие в системе (1.1) силы предполагаются теми же самыми, что и для невозмущенного движения.

Примеры возмущенных движений: движения маятника после его отклонения от нижнего или верхнего положений равновесий; движения спутника по орбитам, незначительно отличающимся от заданной круговой, или движения спутника со скоростями, несколько отличающимися от заданной орбитальной скорости по величине и направлению; движения схвата манипулятора по траектории, отличающейся от заданной, со скоростями, отличающимися от заданных и т.д.

Интуитивно ясно, что, если любое возмущенное движение, близкое к невозмущенному движению в начальный момент времени, будет оставаться близким к нему и в остальные моменты времени, то невозмущенное движение можно считать устойчивым.

Если же «расстояние» от возмущенного движения до невозмущенного движения с течением времени будет увеличиваться и станет не малой величиной, то невозмущенное движение можно считать неустойчивым.

Введем точное определение устойчивости по Ляпунову, которое принято за основное в различных областях науки и техники.

Определение 1.3 (устойчивости по Ляпунову) Невозмущенное движение q_p=ξ(t),
q_p^•=ξ^•(t) системы (1.1) называется устойчивым по Ляпунову относительно величин q = (q₁,…, q_n)^T, q^• = (q₁^•, …, q_n^•)^T, если для любых чисел ε₁, ε₂ > 0, сколь бы малы они ни были,
существуют числа δ₁, δ₂ > 0, зависящие от ε₁, ε₂ и t₀, такие, что для всех решений q(t), q^•(t) уравнений (1.1), начальные условия которых q(t₀), q^•(t₀) удовлетворяют неравенствам
||q(t₀) — ξ₀|| < δ₁, ||q^•(t₀) — ξ₀^•|| < δ₂, (1.7) при всех t ≥ t₀ будут выполняться неравенства ||q(t) — ξ(t)|| < ε₁, ||q^•(t) — ξ^•(t)|| < ε₂. (1.8)
Здесь ||q(t) — ξ(t)|| — евклидова норма вектора x₁(t), характеризующая расстояние между возмущенным и невозмущенным движениями системы.

Геометрическая интерпретация определения устойчивости по Ляпунову в фазовом пространстве q₁,…, q_n , q₁^•,…, q_n^•

На рис.1.2 представлена геометрическая интерпретация определения устойчивости по Ляпунову на фазовой плоскости q, q^• для случая системы с одной степенью свободы (n=1). Начав при t=t₀ движение из точки М₀(q(t₀), q^•(t₀)), лежащей в B_δ-окрестности начальной точки ξ₀, ξ^•₀ невозмущенного движения ξ(t), ξ^•(t), где B_δ: |q(t₀) — ξ₀| < δ₁, |q^•(t₀) — ξ^•0| < δ2, изображающая точка М в случае устойчивости невозмущенного движения ξ(t), ξ^•(t) при t ≥ t₀ не выйдет из B_ε-окрестности данного невозмущенного движения, где B_ε: |q(t) — ξ(t)|<ε₁,
|q^•(t)-ξ^•(t)| < ε₂.

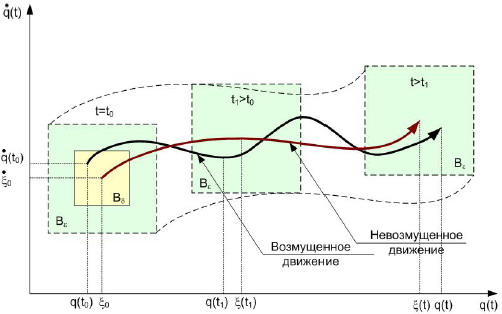
Рис.1.2 Геометрическая интерпретация определения устойчивости по Ляпунову на фазовой плоскости

Комментарии запрещены.