Сеточный метод основывается на замене интервала [v^—, v⁺], на котором определена характеристика g (х, v), ε-сетью v_ε, состоящей из s равномерно расположенных точек v_i.

v^— = v₁ < v₂ < ... < v_s-1 < v_s = v⁺. (1.20)

Совокупность точек (1.20) характеризуется числом ε, равным расстоянию между двумя смежными точками множества v_ε. Очевидно, что для любой непрерывной функции g (х, v) можно выбрать такое число ε₀, что для любых ε < ε₀ выполнение ограничения (1.19) будет соответствовать выполнению системы из s неравенств для фиксированных значений параметра v:

g(x, v_i) ≥ 0, i = 1, 2,…, s. (1.21)

С ростом числа точек дискретизации s выполнение системы неравенств. (1.21) обеспечивает выполнение ограничения (1.19) с любой заданной точностью ε. Однако на практике вопрос выбора конкретного числа точек дискретизации s остается открытым, и разработчику приходится задавать это число на основании своего опыта и знаний физической сущности задачи. Поэтому может оказаться, что выбранное число точен s, достаточное для аппроксимации ограничения (1.19) а заданной точностью ε при одних значениях управляемых параметров х, не обеспечивает выполнения условия (1.21) при других значениях х, т. е. функция g(x, v) при изменении управляемых параметров х может «провалиться» между смежными точками множества v_ε и пересечь положительную полуось v (рис. 1.4).

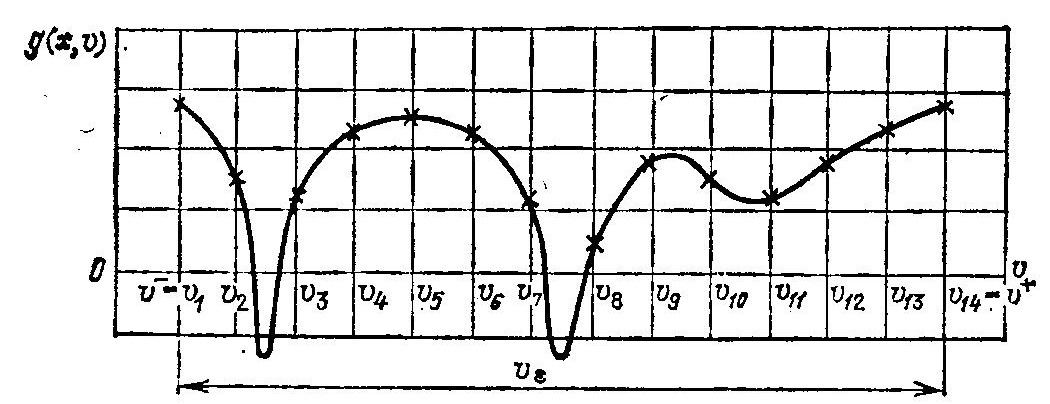
Рис. 1.4. Сеточный метод проверки ограничений, зависящих от параметра v

Для устранения этого недостатка сеточного метода целесообразно для проверки ограничений, зависящих от непрерывно изменяющегося параметра v, использовать принцип гарантированного результата, основная идея которого заключается в том, что неравенство (1.19) проверяется для наиболее неблагоприятного (критического в смысле его выполнения) значения параметра v∈[v^—, v⁺],

g(x, v*) ≥ 0, (1.22)
где
g(x, v*)= min g(x, v). (1.23)

Необходимо отметить, что критическое значение параметра v* зависит от значений управляемых параметров х и является некоторой аналитически неизвестной функцией от них, т. е. v* = v* (х). В связи в этим для каждого фиксированного значения компонент х для проверки условия (1.22) требуется решать задачу одномерного поиска (1.23) для определения критического значения v*. Исследования характеристик электронных схем g (х, v) показывают, что они обычно являются немонотонными функциями от параметра v. Поэтому задача отыскания критического параметра v для каждой из них является задачей глобальной минимизации произвольной кривой. Далее будут рассмотрены численные методы решения задач этого типа, которые основаны на вычислении значений функции g (х, v) в фиксированных точках v_i = 1,2,…, s. Получаемая при этом дискретная сеть имеет неравномерное расположение точек v_i, число которых не задается заранее, а выбирается автоматически в процессе поиска критического значения v* для каждого фиксированного значения управляемых параметров х в зависимости от поведения функции g (х, о) на интервале [v^—, v⁺]. Для сильно изменяющихся функций количество точек дискретизации получается больше, чем для плавных или монотонных кривых. Причем точки v_i располагаются более плотно в подынтервалах, в которых неравенство (1.-19) наиболее критично (в смысле своего выполнения) относительно параметра v (рис. 1.5).

Рис. 1.5. Метод гарантированного результата проверки ограничений, зависящих от параметра о

В дальнейшем будем считать, что ограничения типа (1.19), заданные на интервале [v^—, v⁺], сведены к системе неравенств (1.9) с помощью принципа гарантированного результата (1.22)—(1.23).

Комментарии запрещены.