Во всех случаях, когда имитация функционирования системы осуществляется в условиях случайных воздействий и помех, эксперимент приобретает статистический характер, поскольку обработка результатов имитации должна проводиться с использованием статистических методов.

Статистическое моделирование представляет собой метод получения с помощью ЭВМ статистических данных о процессах в моделируемой системе. Можно сказать, что имитационное моделирование систем в общем случае есть ни что иное, как статистическое моделирование.

Статистическое моделирование охватывает широкий круг вопросов и использует различные методы. Задача осложняется еще тем, что в общем случае исследователь априори не располагает конкретными данными о законах распределения и других статистических характеристиках воздействий и разброса параметров компонентов исследуемой системы (из-за нестабильности технологических процессов, изменения исходных материалов и т.п.). Требуется накопление и обобщение этих сведений, корректировка накопленных статистических данных.

Статистическое моделирование может быть использовано при решении детерминированных задач. Статистический анализ в этом случае применяют после получения, например, оптимального решения детерминированной задачи в номинальном режиме. Окончательному суждению о качестве полученного решения должно предшествовать выполнение статистического анализа, который даст ответ на вопрос об отклонениях выходных параметров от номинальных при замене детерминированной задачи на эквивалентную статистическую.

Одним из широко применяемых методов статистического анализа является метод Монте-Карло. Исходными данными для анализа являются внутренние Х={х₁, х₂,…, х_n} и внешние параметры F= {f₁, f₂, …, f_k} (воздействие среды — сигналы, нагрузка, температура, помехи и т.п.), а результатом решения — определение выходных параметров исследуемого объекта Y= G (X, F).

При производстве изделий и в процессе их эксплуатации имеются неизбежные отклонения от номинальных (требуемых) значений X и F, что приводит к отличию У от Уном. Поэтому окончательное суждение о качестве изделия можно сделать после выполнения статистического анализа, позволяющего оценить рассеяния выходных параметров относительно номинальных (требуемых) значений.

Метод Монте-Карло реализует статистический анализ на основе статистических испытаний. В этом случае исходной информацией являются числовые характеристики закона распределения внутренних параметров X и допустимые диапазоны изменения внешних параметров F, а результатом — числовые характеристики закона распределения У.

Алгоритм метода включает выполнение N-испытаний (опытов). В каждом испытании задаются случайные значения х_i, и f_j в соответствии с их законом распределения и определяются случайные значения параметров у_k.

Схема вычислений методом Монте-Карло представлена на рисунке ниже. В методе многократно (N раз) повторяется детерминированный, одновариантный расчет; N должно быть достаточно большим, чтобы выборка была представительной.

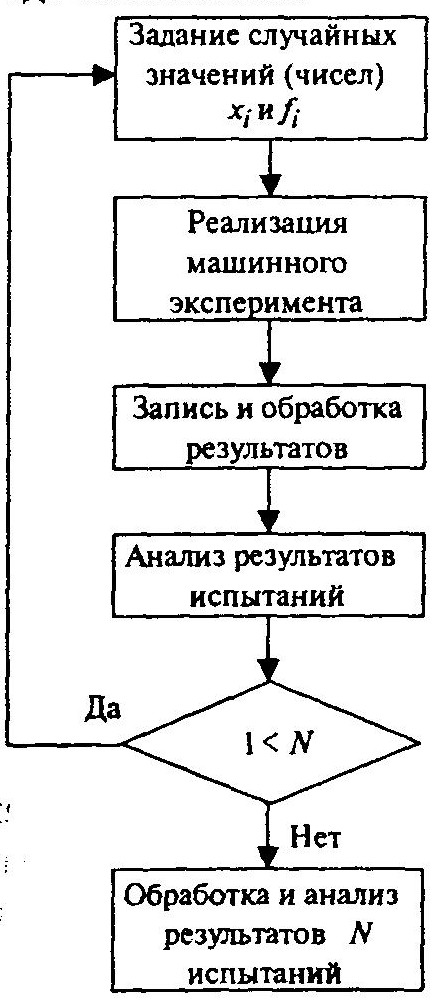
Схема вычислений методом Монте-Карло

Метод статистических испытаний успешно применяется, например, при статистическом анализе микросхем, интегральных схем. Эти схемы имеют большую размерность, нелинейные и корреляционные связи между параметрами, что существенно осложняет прямые аналитические расчеты. Метод Монте-Карло реализует вариантный расчет и, по существу, представляет собой численный метод решения аналитической задачи.

Существует ряд программных комплексов для реализации статистических экспериментов методом Монте-Карло.

Комментарии запрещены.